Метод координат, предложенный в XVII в. Р.Декартом и П.Ферма, является мощным аппаратом, позволяющем переводить геометрические понятия на алгебраический язык. С помощью метода координат можно было бы изложить весь школьный курс геометрии без единого чертежа, используя только числа и алгебраические операции. В основе этого метода лежит понятие “система координат”. Таких систем много, но прямоугольная система вводится в учебнике математике для 5-го класса. В курсе геометрии 9-го класса расширяются первоначальные сведенья, вводятся формулы длины отрезка, координат середины отрезка, уравнения прямой и окружности.

Координаты середины отрезка.

Пусть тогда

Каждая середина координата середины отрезка равна полусумме соответствующих координат его концов.

Вычисление длины отрезка.

Пусть тогда

Уравнение окружности.

где – центр окружности, R – радиус окружности.

Уравнение прямой.

1. – линейная функция, график – прямая. Пусть принадлежат прямой, тогда Решением системы являются значения и Условием перпендикулярности двух прямых является Условием параллельности двух прямых является и

2. Пусть тогда является уравнением прямой, проходящей через точки и

– ось - ось

Перед тем, как приступить к решению задач из учебника, полезно рассмотреть следующие задачи:

Устные задачи:

1. Найти координаты точек, симметричных относительно оси

А (2; 3). Ответ: (2; – 3).
В (-3; 2). Ответ: (-3; -2).
С (-1; -1). Ответ: (-1; 1).
D (-3; -5). Ответ: (-3; 5).
Е (-6; 6). Ответ: (-6; -6).
F (a; b). Ответ: (a; -b).

2. Найдите координаты точек, симметричных относительно оси

А (-1; 2). Ответ: (1; 2).
В (3; -1). Ответ: (-3; -1).
С (-2; -2). Ответ: (2; -2).
D (-2; 5). Ответ: (2; 5).
Е (3; -5). Ответ: (-3; -5).
F (a; b). Ответ: (-a; b).

3. Найдите координаты точек, симметричных относительно начала координат:

А (3; 3). Ответ: (-3; -3).
В (2; -4). Ответ: (-2; 4).
С (-2; 1). Ответ: (2; -1).
D (5; -3). Ответ: (-5; 3).
Е (-5; -4). Ответ: (5; 4).
F (a; b). Ответ: (-a; -b).

4: Является ли уравнением окружности уравнение:

а) Ответ: да, если
б) Ответ: нет.
в) Ответ: да.
г) Ответ: нет.
д) Ответ: нет.
е) Ответ: нет.

5. Окружность задана уравнением Пересекает ли эту окружность:

а) ось Ответ: нет.
б) ось Ответ: да.
в) прямую Ответ: да.
г) прямую Ответ: нет.
д) окружность Ответ: нет.

6. Напишите уравнение окружности:

а) проходящей через начало координат, радиус 1.

Ответ: а и b – любые.

б) проходящей через точки (1; 0) и (-5; 0), радиус 10.

Ответ:

в) проходящей через точки (-2; -1). (3; 0), (0; 1).

Ответ:

г) проходящей через точки (1; -1), (2; -2) и касающейся оси

Ответ:

Для закрепления теоретического материала можно предложить учащимся следующие задачи:

1. Напишите уравнение прямой, проходящей через точки:

а) (-2; 3) и (3; 2). Ответ:

б) (3; 0) и (3; 2). Ответ:

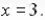
в) (-3; -1) и (7; 1). Ответ:

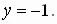
1. Напишите уравнение прямой проходящей через точку (3; -1) и

   а) параллельной оси Ответ:

   б) параллельной оси Ответ:

   в) образующей с осью угол Ответ:

   г) параллельной прямой Ответ:

   д) перпендикулярной прямой Ответ:

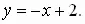
2. Найдите центр и радиус окружности, если задано уравнение:

а) Ответ:

б) Ответ:

в) Ответ:

г) Ответ:

д) Ответ:

Из учебника “Геометрия 7-9” Л.С. Атанесяна решить задачи № 947, 951, 971-974, 980.

Дополнительно можно решить следующие задачи:

1. Даны две смежные вершины квадрата А(3; -7) и В(-1; 4). Найдите его площадь.

   Ответ: 137.

2. Даны две противоположные вершины квадрата Р(3; 5) и Q(1; -3). Найдите его площадь.

   Ответ:

3. Вычислите площадь правильного треугольника, две вершины которого А(-3; 2), В(1; 6).

   Ответ:

4. Даны три вершины А(3; -7), В(5; -7), С(-2; 5) параллелограмма ABCD, четвёртая вершина которого D противоположна В. Найдите длину диагоналей этого параллелограмма.

   Ответ: 13 и 15.

5. Сторона ромба две его противоположные вершины Р(4; 9) и

   Q(-2; 1). Найдите площадь этого ромба.

   Ответ: 150.

6. Даны вершины треугольника А(3; 6), В(-1; 3), С(2; -1). Вычислите длину его высоты опущенной из вершины С.

   Ответ: 5.

7. Три вершины параллелограмма А(3; 7), В(2; -3), С(-1; 4). Вычислите длину его высоты, опущенной из вершины В на стороны АС.

   Ответ: 7,4.

8. Площадь треугольника S=4, две его вершины А(2; 1) и В(3; -2), а третья вершина С лежит на оси

Определите координаты вершины С.

Ответ: (-5; 0) или

В учебнике “Геометрия 7-9” Л.С. Атанесяна в теме “Метод координат” не рассматривается вывод формулы площади треугольника через координаты его вершин. Однако, этот вопрос полезен для учащихся, интересующихся математикой.

Задача. Найдите площадь треугольника АВС, если

1) Найдём площадь трапеции

2) Найдём площадь трапеции

3) Найдём площадь трапеции

4)

После упрощения получим

Рассмотрена задача, когда вершины треугольника расположены в первой координатной четверти. Можно предложить учащимся получить эту формулу при другом расположении вершин А, В, С.

Задача 1. А (2; -3)

В (3; 2) Найти площадь треугольника АВС.

С (-2; 5) Ответ: 14.

Задача 2. А (1; 2)

В (-2; 5) Найти площадь треугольника АВС.

С (4; -2) Ответ: 1,5.

Задача 3. А (3; 4)

В (6; 6) На оси найти точку С так, чтобы площадь

треугольника АВС была равна 5.

Ответ: или

Задача 4. А (3; -4)

В (-2; 3) Найти площадь треугольника АВС.

С (4; 5) Ответ: 16.

Задача 4. А (-3; 2)

В (5; -2) Найти площадь треугольника АВС.

С (1; 3) Ответ: 12.

На уроках информатики полезно предложить учащимся составить программу для решения задач с использованием метода координат (см. Приложение 1).