Урок по теме "Способы решения тригонометрических уравнений. Итоговый урок"
"Уравнения будут существовать вечно".
А.Эйнштейн.
Цели урока:
Образовательные:
- повторить способы решения некоторых видов тригонометрических уравнений;
- систематизировать полученные знания, активизировать самоконтроль, взаимоконтроль.
Развивающие:
- уметь применять полученные знания для решения тригонометрических уравнений;
- развивать математическое мышление.
Воспитательная:
- воспитать интерес к математике и к дисциплинам умственного труда.
Тип урока: итоговый урок
Формы работы учащихся: фронтальная, индивидуальная
Необходимое оборудование: интерактивная доска, мультимедиа проектор, карточки с устными и подготовительными упражнениями, 4 варианта самостоятельной работы.
Ход урока
- Организационный момент.
- Устные упражнения.
- Подготовительные упражнения.
- Повторение методов решения тригонометрических уравнений.
- Самостоятельная работа.
- Подведение итогов урока.
- Домашнее задание.
-
Организационный момент.
Приветствие учителя, отметить отсутствующих, проверить подготовку к уроку. Сообщить тему и цель урока. В дальнейшем все задания выводятся на интерактивную доску.
- Устные упражнения.
- Что называется арксинусом, арккосинусом, арктангенсом числа? Привести примеры.
- Для каких чисел определен арксинус, арккосинус, арктангенс.
- Написать формулы нахождения корней уравнений: sin x = a, cos x = a, tg x = a.
- При каких значениях а уравнения sin x = a, cos x = a, tq x = a имеют решения?
- Вспомнить как вычисляются обратные тригонометрические функции.
- Вычислить:
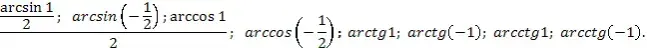 Решить простейшие уравнения:
Решить простейшие уравнения: 
![]()
ctg x=0; cos x=1
- Подготовительные упражнения.
- Пользуясь формулами сложения преобразовать выражения:

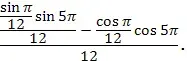
 .
.
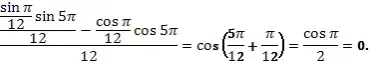

- Повторение методов решения тригонометрических уравнений.
- Решение методом введения новой переменной.
-
4sin2x+11sinx - 3 =0.
Введём новую переменную: t=sin x, t
 приходим к квадратному уравнению:
приходим к квадратному уравнению:4t2+11t - 3=0.
Корни данного уравнения t1= -3; t2=
 .
.Делаем обратную замену с учетом, что t
 sin x=
sin x= . Решаем данное уравнение:
. Решаем данное уравнение:x = arcsin
 + 2
+ 2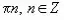 .
.x =
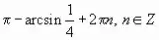 .
.Ответ можно записать в следующем виде:
a) x =
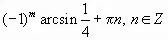 .
. - 5sin2x+6cos x - 1 =0.
Из основного тригонометрического тождества sin2x=1 - cos2x, следовательно исходное уравнение примет вид: -5cos2x+6cos x - 1=0.
Введём новую переменную t=cos x, t![]()
![]() .
Приходим к квадратному уравнению:
.
Приходим к квадратному уравнению:
-5t2+6t - 1=0. Корни данного уравнения t1=1; t2= ![]() . Оба корня подходят.
Делаем обратную замену.
. Оба корня подходят.
Делаем обратную замену.
cos x=1
Частный случай х=![]() .
.
cos x=![]() .
.
![]()
![]() .
.
- Решение однородного уравнения.
- cos2x+4sin2x=2sin2x.
Перепишем уравнение с учётом формулы двойного угла cos2x+4sin2x=4sin xcos x. Разделим обе части уравнения на cos2x![]() Получим уравнение 4tg2x-4tg2x+1=0. Введём новую переменную: t=tgx, уравнение примет вид 4t2 - 4t+1=0. Корень данного
уравнения: t= 0,5. Сделаем обратную замену tg x=0,5. Ответ: х = arctg.
Получим уравнение 4tg2x-4tg2x+1=0. Введём новую переменную: t=tgx, уравнение примет вид 4t2 - 4t+1=0. Корень данного
уравнения: t= 0,5. Сделаем обратную замену tg x=0,5. Ответ: х = arctg.
- Введение вспомогательного угла.
-
sin x+7cos x=5.
Решим методом вспомогательного угла. Найдём
 Разделим обе части на
Разделим обе части на 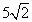 , получим
, получим  . sin
. sin  , cos
, cos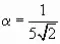 . Тогда tg
. Тогда tg 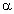 =7 и
=7 и 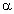 =arctg7. Применим формулу синуса суммы, получим:
=arctg7. Применим формулу синуса суммы, получим:sin(x+
 )=
)=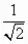 , отсюда x+
, отсюда x+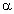 =
=
x=
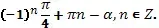
Ответ:
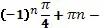 arctg7.
arctg7. 
Разделим обе части на 2, получим ![]()
![]() Уравнение примет вид
Уравнение примет вид ![]() Применим формулу синуса разности получим: sin(x -
Применим формулу синуса разности получим: sin(x - ![]() )=
)=![]() . (x -
. (x - ![]() )=. Ответ: x=
)=. Ответ: x=![]() . Ответ можно записать
в следующем виде: х=
. Ответ можно записать
в следующем виде: х=![]()
-
Разложение на множители.
sin2x - sin x=0.
Вынесем sin x за скобки, получим уравнение: sin x(sin x - 1) = 0; sin x=0 или sin x - 1 =0.
Ответ:x=
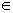 n , n
n , n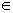 Z. x=
Z. x=
- Применение различных формул.
-
sin 4x cos2x - cos4x sin2x=0.
Применяем формулу синуса разности. Подобный пример уже рассматривался.
- 3sin2x - 4cosx + 3sinx - 2=0.
Решение: 6sin x cosx+3sinx - 4cosx - 2=0,
3sinx(2cosx+1) - 2(2cosx+1)=0.
(2cosx+1)(3sinx - 2)=0.
2cosx+1=0 или 3sinx - 2=0.
cos x=![]() , x=
, x=![]()
sin x=![]() , x=
, x= ![]() .
.
Ответ:![]()
- Самостоятельная работа (10 - 15 мин.).
|
1 Вариант.
|
2 Вариант.
|
|
3 Вариант.
|
4 Вариант.
|
-
Подведение итогов урока.
Данный урок последний перед контрольной работой по теме: " Решение тригонометрических уравнений". На уроке рассмотрены основные методы решений тригонометрических уравнений, разбираемые в школе.
- Домашнее задание (по учебнику Колмогорова А.Н.) №166(г); 168(г); 169(г); 170(г); 172(г).