Урок математики. Тема: "Сложение дробей с одинаковыми знаменателями". 4-й класс
Образовательная программа: «Школа 2000…»
Класс: 4.
Тип урока: ОНЗ.
Цели:
- сформировать умение складывать дроби с одинаковыми знаменателями;
- повторить понятие дроби, закрепить умение читать и сравнивать дроби;
- тренировать вычислительные навыки, умение решать задачи на нахождение части;
- формировать УУД.
Мыслительные операции, необходимые на этапе проектирования: анализ, сравнение, аналогия, обобщение.
Ход урока
1. Мотивация к учебной деятельности
- Сегодня у нас урок ОНЗ - урок открытия новых знаний. По какому плану вы открываете новые знания?
План:
- Исследуем и наблюдаем.
- Открываем новое знание.
- Применяем знания.
- Контролируем.
- Оцениваем.
- Всё правильно. А сначала повторим то, что нам понадобится для изучения нового.
2. Актуализация знаний и фиксация затруднения в пробном действии
На доске записаны числа:
![]()
- На какие две группы можно разбить эти числа? (Натуральные и дроби)
- Что вы уже знаете о натуральных числах и что умеете делать с ними? (Знаем, что такое натуральные числа; умеем их записывать; отмечать на числовом луче; сравнивать; складывать; вычитать; умножать; делить.)
- Что вы уже знаете о дробях и что умеете делать с дробями? (Знаем, что такое дробь; умеем записывать дроби; изображать графические модели дробей, отмечать на числовом луче; сравнивать дроби; находить части числа и число по его части; части, которую одно число составляет от другого.)
- Проверим, насколько хорошо вы умеете это делать.
Проводится опрос-тест с помощью программы Plickers:
- Вычисли 5/8 от 16.
- Вычисли 3/11 от 33.
- Вычисли 7% от 600.
- Найди число, 2/9 которого равны 8.
- Найди число, 5% которого равны 35.
- Для чего служат натуральные числа, а для чего - дроби? (Натуральные числа служат для счёта предметов, а дроби - для выражения их частей.)
- Интересно, Что ещё математики древности высоко ценили умение оперировать дробями. Вот одна старинная задача. У Пифагора спросили однажды, сколько у него учеников. Он ответил: «Половина моих учеников изучают прекрасную математику, четверть исследуют тайны природы, седьмая часть упражняет силу духа. Добавьте ещё к ним трёх юношей, их которых Теон самый способный».
- Чтобы ответить на вопрос этой задачи, надо сложить несколько чисел. Трудность в том, что эти числа - дроби!
- Сможете ли вы решить эту задачу? (Нет.)
- Что вы ещё не умеете делать? (Складывать дроби.)
- Сформулируйте цель нашего урока. (Научиться складывать дроби.)
- Но дроби бывают разные: с одинаковыми знаменателями и разными. Сегодня вы научитесь складывать дроби с одинаковыми знаменателями.
- Найдите среди чисел на доске дроби с одинаковыми знаменателями. (![]() )
)
- Что показывает каждое число в записи дроби? (Под чертой - знаменатель, он показывает, на сколько равных частей разделили целое. Над чертой - числитель, он показывает, сколько равных долей взято.)
- Что, значит, сложить числа? (Объединить в одно целое.)
- Попробуйте сложить эти дроби.
![]()
Что у вас получилось? (![]() )
)
- Кто не смог получить ответ? Почему? (Мы не можем сложить дроби ![]() .)
.)
- Кто из получивших ответ сможет доказать, что ответ верный? (Не можем доказать)
3. Выявление места и причины затруднения
- Какое задание вы выполняли? (Складывали дроби ![]() .)
.)
- Что особенного в записи этих дробей? (Одинаковые знаменатели.)
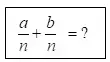
- Как пробовали выполнить сложение дробей? (Учащиеся объясняют свои действия.)
- Почему возникли затруднения? (Не знаем единого способа сложения дробей.)
4. Построение проекта выхода из затруднения
- Какова же цель урока? (Научиться складывать дроби и построить алгоритм сложения дробей с одинаковыми знаменателями.)
- Уточним тему урока. (Сложение дробей с одинаковыми знаменателями.)
- Что вам может помочь? (Графические модели. Числовой луч.)
На доске составляется план выхода из затруднения.
План:
1) Выполнить сложение с помощью графических моделей.
2) Проанализировать результат.
3) Сформулировать вывод. Записать его в общем виде.
4) Оформить алгоритм.
5. Реализация построенного проекта
- Сейчас вы будете работать в группах по составленному плану. Вспомните правила работы в группе.
У каждой группы в конвертах лежат необходимые материалы для работы: графическая модель, блоки для составления алгоритма, карточки для составления опорного конспекта.
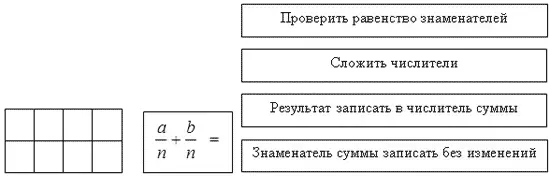
- Выполнить сложение с помощью графической модели. На реализацию плана отводится 5 минут.
- Итак, сравним опорные конспекты, которые вы дополнили. Конспекты вывешиваются на доске. Что можете сказать? (Получились одинаковые конспекты.)
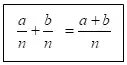
- Чтобы проверить правильность выполнения задания посмотрите видео-урок (отрывок) Ю.К.Грачёвой на портале «Знайка».
- Правильно ли вы составили опорные конспекты?
- А теперь посмотрим, какие алгоритмы получились в группах.
Представитель одной группы зачитывает алгоритм. Остальные группы соглашаются или не соглашаются с ним. В ходе обсуждения на доске появляется правильный алгоритм.
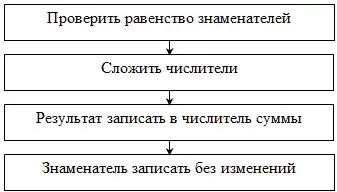
- Можно ли данный способ (алгоритм) применить для выполнения пробного действия? (Да.)
- Правило сложения дробей есть в учебнике. С ним вы можете сравнить свои выводы. Откройте учебник и прочитайте правило на стр.7. Сравните с вашим результатом. (Похожи.)
6. Первичное закрепление во внешней речи
- Чем вы пользовались, чтобы сложить дроби? (графической моделью)
- Расскажите, как складывали дроби с помощью числового луча.
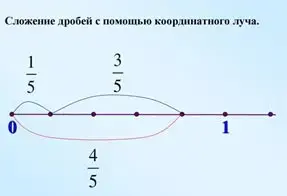
(Объяснения детей.)
- Откройте в учебнике № 2, 3 на стр. 7. Выполните задания, работая в парах с проговариванием.
Проверка результатов.
- Где возможна ошибка при решении таких примеров? (При сложении чисел в числителях и на применение алгоритма.)
- Каким правилом пользовались для сложения дробей?
7. Самостоятельная работа с самопроверкой по эталону
- Проверим, как вы научились ли вы складывать дроби с одинаковыми знаменателями? Для этого проведём самостоятельную работу. № 4 на стр.7.
Проверка по эталону.
- Кто допустил ошибки? В каком месте, и по каким причинам?
- Что нужно сделать, чтобы не допускать ошибки? (Тренироваться.)
- Какое задание в учебнике можно использовать для тренировки? (№ 7, стр. 8)
- Кто выполнил верно?
8. Включение в систему знаний и повторение
- Где вы можете применить новый способ? (При решении уравнений, задач.)
Задача на слайде:
«Помидорами занято 4/11 поля, а помидорами - 2/11 поля. Какая часть поля занята огурцами и помидорами?»
- Прочитайте текст задачи. Выполните анализ. Решите задачу.
Проверка по эталону на слайде.
- Кто допустил ошибки? В каком месте, и по каким причинам?
- Кто выполнил верно?
- Каким правилом пользовались для сложения дробей?
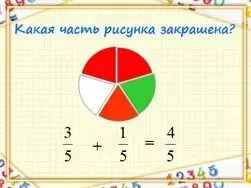
На слайде иллюстрация сложения дробей.
- Какая часть рисунка закрашена?
- Как посчитали?
9. Рефлексия учебной деятельности на уроке
- Какова была цель сегодняшнего урока? (Научиться складывать дроби с одинаковым знаменателем. Построить алгоритм сложения дробей с одинаковыми знаменателями.)
- Достигли ли вы этой цели? (Да.)
- Сможете ли вы теперь решить задачу Пифагора? Почему?
- Да, вам ещё многому надо научиться!
Слайд.

Домашнее задание: стр. 8, № 7, 8.