Урок-практикум "Графическое решение уравнений, содержащих функцию y=√х (функцию квадратного корня)". 8-й класс
Базовый учебник: Алгебра 8 класс. Учебник для общеобразовательных учреждений/ А. Г. Мордкович.
Цель урока: применить алгоритм решения уравнений графически к функции у = ![]() .
.
Задачи:
- Обучающая: способствовать закреплению знаний свойств функции у =
 , умение строить график этой функции, использовать
алгоритм графического решения уравнений применительно к графику квадратного корня из неотрицательного числа.
, умение строить график этой функции, использовать
алгоритм графического решения уравнений применительно к графику квадратного корня из неотрицательного числа. - Развивающая: развитие умения правильно оперировать полученными знаниями, логически мыслить; развитие инициативы, умения принимать решения, не останавливаться на достигнутом; работа на интерактивной доске, познавательная активность.
- Воспитывающая: воспитание познавательного интереса к предмету; к самостоятельности при решении учебных задач; воспитание воли и упорства для достижения конечных результатов.
Тип урока: урок практикум.
Методы:
- словестные: фронтальная работа
- наглядные алгоритм, графики.
- практические: индивидуальная, парная и групповая работа, тренировочная самостоятельная работа.
Оборудование: учебник, рабочая тетрадь, раздаточный материал, школьная доска, интерактивная доска.
План урока.
1. Организационный момент. 1 мин
2. Проверка домашнего задания. 5 мин
3. Актуализация знаний. Устная работа с классом. 7 мин
4. Закрепление материала 20 мин
5. Тренировочная самостоятельная работа. 8 мин
6. Постановка домашнего задания. 3 мин
7. Рефлексия. 1 мин
8. Итог урока. 1мин
Ход урока
1. Организационный момент.
2. Проверка домашнего задания. (Учащиеся проверяют домашнюю работу, сверяясь с эталоном, оценивают правильность и полноту выполнения согласно критериям, ставят оценку).
Для №13.3 Сопоставьте график который получился у вас дома с одним из графиков. Слайд 2. Из данных утверждений (приложение 1 у каждого ученика) выберите те свойства, которые подходят для
функции у = - ![]() :
:
С помощью графика найдите: Слайд 3
а) значения у при х = 1; ![]() ; 9; (выборочно)
; 9; (выборочно)
б) значения х, если у = 0; -2; -4; (выборочно)
в) наименьшее и наибольшее значения функции на отрезке ![]() ;
;
г) при каких значениях х график функции расположен выше прямой у = -2. Ниже прямой у = -2.
3. Актуализация знаний. Устная работа с классом.
Устная работа:
1. Принадлежит ли графику функции у =![]() точки
точки
А(2; ![]() ); В(1; 0); С(6,25; 2,5); Д(-9; 3).Слайд 4
); В(1; 0); С(6,25; 2,5); Д(-9; 3).Слайд 4

2. Найдите наименьшее и наибольшее значение функции у =![]() Слайд 5
Слайд 5
а) на отрезке ![]() ;
;
б) на полуинтервале [4; 7);
в) на луче [0; ![]() )
)
3. Решите уравнение по заданному графику: х2 = х +2. Слайд 6
Учащиеся вспоминают (7 класс) алгоритм решения уравнений данного типа, проговаривая, что является корнем уравнения. Как данное задание мы будем применять на уроке.
Ученики говорят тему урока(на доске записана), формулируют цель,
4. Закрепление материала
Задание 1. Итак, повторив алгоритм решения уравнений графически выполним задание № 13.9 (б).
(ученик у доски, остальные в тетради)
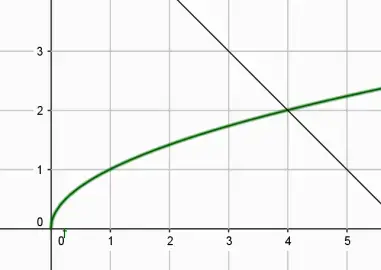
![]() = 6 - х;
= 6 - х;
1) Рассмотрим две функции у = ![]() и у = 6 - х
и у = 6 - х
2) Построим график функции у = ![]() ,
,
х 0 1 4 у 0 1 2
3) Построим график функции у = 6 - х,
х 0 2 у 6 4
4) По графику устанавливаем, что графики пересекаются в одной точке А(4; 2). Проверим принадлежность данной точки нашим функциям.
Ответ: х = 4. Слайд 7
Задание 2 Решить уравнение графически: два человека у доски остальные на местах выполняют соответственно свои варианты самостоятельно. Совместно устраняют в ходе проверки
обнаруженные пробелы (на доске и на листах учеников готовая памятка с построенным графиком линейной функции). Построение графика квадратного корня ![]() ученики выполняют самостоятельно. И записывают ответ.
ученики выполняют самостоятельно. И записывают ответ.
|
Памятка 1 вариант а) - Рассмотрим функции:__________________ у = х - 2,
Ответ: Оцените себя, отметив уровень этого показателя. Понимание: - ______________+ |
Памятка 2 вариант б) - Рассмотри функции:____________________ у = 2 - 3х
Ответ: Оцените себя, отметив уровень этого показателя. Понимание: - ______________+ |
Задание 3. Решить графически систему уравнений
(работа выполняется в парах используя приложение № 2)
![]()
После выполнения задания учащиеся проверяют свое решение, сравнивая с эталоном. Слайд 8
Встаньте те кто справился с данным заданием.
Физкультминутка для глаз. Слайд 9
Задание 4. Работа в группах(задания дифференцированы, приложение 3): Слайд 10
Задание 1 группе: Докажите, что графики функций у = ![]() и у = х + 0,5 не имеют общих точек. Слайд
11
и у = х + 0,5 не имеют общих точек. Слайд
11
Р е ш е н и е
Чтобы доказать, что графики функций y = ![]() и у = х + 0,5 не имеют общих точек, достаточно их
построить.
и у = х + 0,5 не имеют общих точек, достаточно их
построить.

Задание 2 группе: Сколько корней имеет данное уравнение ![]() = х + b Слайд 12
= х + b Слайд 12
Р е ш е н и е
а) Построим график функции y =![]() и будем относительно него передвигать прямые вида y = x + b.
Это параллельные прямые, которые образуют острый угол с положительным направлением оси абсцисс.
и будем относительно него передвигать прямые вида y = x + b.
Это параллельные прямые, которые образуют острый угол с положительным направлением оси абсцисс.

Таким образом, очевидно, что уравнение ![]() = x + b может иметь один, два корня, а может и не иметь корней.
= x + b может иметь один, два корня, а может и не иметь корней.
Задание 3 группе: Сколько корней имеет данное уравнение ![]() = - х + b
= - х + b
Р е ш е н и е
Прямые вида y = -x + b - это параллельные прямые, которые образуют тупой угол с положительным направлением оси абсцисс.
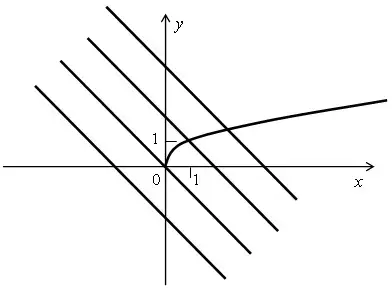
Получаем, что уравнение ![]() = -x + b имеет либо один корень, либо не имеет корней.
= -x + b имеет либо один корень, либо не имеет корней.
Обсуждение решений каждой группы.( Для готовых графиков квадратного корня на интерактивной доске учащиеся показывают свои решения)
5. Тренировочная самостоятельная работа.
Фамилия имя___________________________класс______
В а р и а н т 1
1 . По графику функции у = ![]() найдите:
найдите:
а) значение функции при х = 3, у =____
б) значение аргумента, которому соответствует значение y = 1,8; х = _____
2. Принадлежит ли графику функции y = ![]() точка:
точка:
а) А (36; 6); ______ б) В (-9; 3)_______?

3. Решите уравнение графически - ![]() = - х
= - х
На листочках с самостоятельной работой поставьте:
1 - если на уроке вам было интересно и понятно;
2 - интересно, но не понятно;
3 - не интересно, но понятно;
4 - не интересно, не понятно.
Фамилия имя___________________________класс______
В а р и а н т 2
1. По графику функции y = ![]() найдите:
найдите:
а) значение функции при х = 5; у =
б) значение аргумента, которому соответствует значение у = 1,5; х =
2. Принадлежит ли графику функции y = - ![]() точка:
точка:
а) А (81; -9)______ б) В (-16; 4)_______

3. Решите уравнение графически ![]() = х
= х
На листочках с самостоятельной работой поставьте:
1 - если на уроке вам было интересно и понятно;
2 - интересно, но не понятно;
3 - не интересно, но понятно;
4 - не интересно, не понятно.
Проверяем работу с помощью эталона. Слайд 13 Выясняем проблемы по данной теме.
6. Постановка домашнего задания.
№ 13.9(г), № 13.11(г), № 13.16(рис 7 опишите свойства функции)
7. Рефлексия.
На листочках с самостоятельной работой поставьте:
1 - если на уроке вам было интересно и понятно;
2 - интересно, но не понятно;
3 - не интересно, но понятно;
4 - не интересно, не понятно.
8. Итог урока.
Урок я хочу закончить словами древнегреческого ученого Фалеса:
Что быстрее всего? - Ум
Что мудрее всего? - Время
Что приятнее всего? Достичь желаемого.
Я думаю, мы с вами достигли желаемого? Еще раз вспомнли функцию квадратного корня из неотрицательного числа и применили алгоритм решения уравнения графически к этой функции. Но ребята, кроме у =
![]() в дальнейшем мы будем рассматривать более сложные функции, например у =
в дальнейшем мы будем рассматривать более сложные функции, например у = ![]() у =
у = ![]() -1 у =
-1 у = ![]() +5.
+5.
Так что перспектива развития ваших знаний велика. Дерзайте.
Приложение № 1
Для номера 13.3 Сопоставьте график который получился у вас дома с одним из графиков. Слайд 2
Из данных утверждений выберите те свойства, которые подходят для функции у = - ![]() :
:
- Область определения функции - луч [0; +
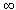 )
) - Область определения функции - луч ( +
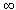 ; 0]
; 0] - у = 0 при х = 0, у < 0 при х > 0
- Функция убывает на луче [0; +
 )
) - Функция возрастает на луче [0; +
 )
) - унаиб = 0, унаим не существует
- Функция непрерывна на луче [0; +
 )
) - Область значения функции - луч [0; +
 )
) - Область значения функции - луч (-
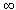 ; 0]
; 0] - Функция выпукла вниз.
- Функция выпукла вверх.
Приложение 2
Работа в парах Задание № 3
Решите графически систему уравнений:![]()

Приложение 3
Работа в группах Задание № 4
Задание 1 группе: Докажите, что графики функций у = ![]() и у = х + 0,5 не имеют общих точек.
и у = х + 0,5 не имеют общих точек.

Задание 2 группе: Сколько корней имеет данное уравнение ![]() = х + b
= х + b

Задание 3 группе: Сколько корней имеет данное уравнение ![]() = - х + b
= - х + b


