Урок геометрии по теме "Задачи на построение". 7-й класс

Цели уроков:

Образовательные:

• Познакомить учащихся  с основными   задачами на построение с использованием циркуля и линейки без делений;
• Рассмотреть основные геометрические построения: деление отрезка пополам, построение   угла равного данному, построение биссектрисы угла, построение перпендикуляра к  прямой.

Развивающие:

• развивать память, внимание, логическое мышление  
• развить практические  умения  и навыки   в использовании чертёжных инструментов   при решении геометрических задач.

Воспитательные:

• сформировать познавательный интерес к предмету;
• продолжить формирование культуры общения и коммуникативных умений учащихся;
• повысить активность и самостоятельность учащихся при выполнении заданий.

Тип уроков: урок ознакомления с новым материалом, урок отработки практических навыков, урок закрепления навыков и умений.

1. Вступительная лекция:

• Исторические сведения;
• Инструменты для построения;

2. План решения задач на построение;

3. Выполнение простейших задачи на построение;

4. Решение задач на построение;

5. Примеры задач на построение

1. Вступительная лекция (слайд 3):

Исторические сведения:

Задачи на построение вошли в практику задолго до того, как геометрия и вообще математика стала настоящей теоретической наукой. И в Вавилоне, и в Древнем Египте в IV-II тысячелетиях до н.э. уже существовала практическая математика (в виде правил записи чисел, т.е. системы счисления, и правил различных вычислений), и практическая геометрия - геометрия в изначальном смысле слова: измерение земли. Но и при измерениях, и при строительных работах нужны были построения. Египтяне, по-видимому, знали, что треугольник со сторонами 3, 4, 5 - прямоугольный, так что с помощью веревки, разделенной узлами на 12 = 3 + 4 + 5 частей, можно построить прямой угол. Древние греки так и называли египетских геометров "гарпедонаптами" - дословно, "натягивателями веревок". С другой стороны, уже вавилоняне рассматривали геометрические задачи теоретического характера, использовали подобие фигур, знали "теорему Пифагора" более чем за тысячу лет до Пифагора. Однако математические и геометрические знания в Вавилоне, Египте, да и в Греции вплоть до VII в. до н.э. были эмпирическими, основанными только на опыте и наблюдениях.

Геометрия как наука, да и вообще наука как таковая, появилась во времена Фалеса (VII-VI вв. до н.э.), который впервые осознал необходимость доказательства математических теорем. После Аристотеля (IV в. до н.э.) название "геометрия" закрепилось за математической наукой, а "землемерию" было дано свое наименование: "геодезия" - деление, межевание земель. К концу IV века до н.э. в математике, которая и сводилась, главным образом, к геометрии, накопилось много понятий, фактов, доказательств, методов и даже теорий - таких, как метод исчерпывания и теория отношений Евдокса, теория конических сечений и др. Аристотелем уже были разработаны основные принципы построения общей аксиоматической теории. И на рубеже IV и III веков Евклид создал 13-томный труд, "Stoicheia" - стихии, элементы по-гречески, "Elementa" (элементы) на латыни, "Начала" по-русски. "Начала" вот уже третье тысячелетие служат образцом научного трактата (аксиоматического изложения теории) и учебника, и не только по геометрии.

Зачем Евклиду потребовались построения? Зачем вообще в геометрии построения? Зачем нужно учиться решать задачи на построение (Евклид называл их проблемами, в отличие от теорем)?

Доказательства, да и вычисления в геометрии, как правило, опираются на какие-то дополнительные построения. Конечно, их можно просто описать, но нужно быть уверенными, что они действительно возможны. Еще важнее то, что определения геометрических объектов и понятий при строгом изложении теории должны сопровождаться доказательствами их существования. А главный метод доказательства существования в геометрии - конструктивный, т. е. построение нужного объекта с последующим доказательством, что построенный объект удовлетворяет нужным условиям.

Решение задач на построение развивает геометрическое мышление гораздо полнее и острее, чем решение задач на вычисление, и способно вызвать увлечение работой, которое приводит к усилению любознательности и к желанию расширить и углубить изучение геометрии.

Несмотря на богатое историческое прошлое, проблема решения задач на построение остается актуальной и в 21-м веке. В наше время бурно развиваются компьютерные технологии с применением графических редакторов для рисования геометрических объектов. Средства создания геометрических объектов изменились в связи с появлением новых компьютерных технологий. Однако, как и в глубокой древности, основными элементами при построении геометрических объектов остаются окружность и прямая, другими словами циркуль и линейка. С появлением новых компьютерных технологий возникли новые проблемы построения с использованием тех же объектов - прямой и окружности. Вот почему проблема решения задач на построение становится ещё более актуальной.

Инструменты для построения: (слайд 4):

Инструменты, употребляемые для выполнения геометрических построений, весьма разнообразны. К основным инструментам принадлежат линейка и циркуль, служащие для проведения прямых линий, одиночных, параллельных и перпендикулярных, и окружностей. Угольник есть вспомогательный инструмент, так как, имея линейку и циркуль, можно строить параллельные и перпендикулярные прямые. К вспомогательным инструментам относится также миллиметровая шкала, которую можно построить с помощью циркуля и линейки, отложив на прямой линии циркулем одинаковые сантиметровые отрезки и разделив каждый из этих отрезков на 10 равных между собою частей. Транспортир есть уже самодеятельный инструмент, так как точное в геометрическом смысле градуирование любой дуги на произвольное число равных частей с помощью линейки и циркуля невозможно.

С глубокой древности повелось допускать к исполнению геометрических построений только циркуль и линейку, т. е. приборы, позволяющие проводить прямые линии и окружности.

Задачи на построение с помощью циркуля и линейки - это задачи, в которых были очень сильны древнегреческие математики. Линейка считается без делений, даже если они на ней указаны. С помощью линейки можно проводить прямые линии, но нельзя измерять и откладывать отрезки, нельзя также, пользуясь ее краями, проводить параллельные линии. Таким образом, линейку можно использовать для проведения произвольной прямой, прямой через данную точку, прямой через две данные точки.

С помощью циркуля можно провести произвольную окружность, можно провести окружность с данным центром и данного радиуса. Можно также на данной прямой отложить отрезок, равный данному.

2. План решения задач на построение (слайд 5)

Решение задач на построение - это описание последовательности шагов с использованием основных простейших построений, которая приводит к построению искомой фигуры. Чтобы найти эту последовательность шагов, т.е. составить план решения задачи, обычно поступают так. Предполагают, что задача решена, делают примерный чертеж искомой фигуры, отмечают те отрезки и углы, которые известны из условия задачи, и стараются определить, к нахождению какой точки (прямой, угла) сводится решение задачи. После этого стремятся найти такую зависимость между данными и искомыми величинами, которая позволяет построить искомую точку (прямую, угол), и составляют план построения. Составление плана - самая важная часть задачи, ее называют анализом.

Выполнив анализ, наметив план, описывают само построение. Оно может содержать лишь основные построения и элементарные действия с циркулем и линейкой.

Далее требуется привести доказательство того, что построенная фигура удовлетворяет всем условиям задачи и, кроме того, проделать исследование, т.е. выяснить, всегда ли (при любых ли данных) описанное построение возможно, нет ли частных случаев, в которых построение упрощается или делается невозможным.

Таким образом, решение задачи на построение состоит из 4-х частей: анализ, построение, доказательство, исследование. Анализ опускается в простых задачах или в тех, решение которых уже известно.

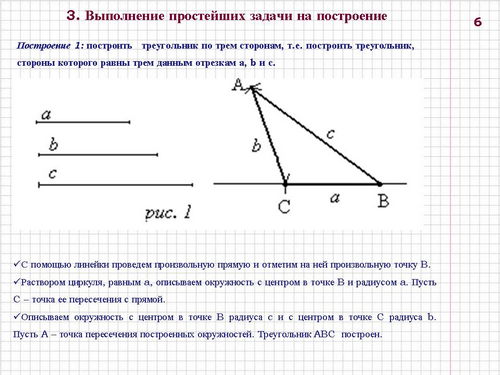
3. Выполнение простейших задачи на построение

Построение 1: построить треугольник по трем сторонам, т.е. построить треугольник, стороны которого равны трем данным отрезкам а, b и с. Построение треугольника по трем сторонам сводится к построению последовательно трех отрезков, равных данным (слайд 6).

Доказательство следует непосредственно из равенства сторон построенного треугольника заданным отрезкам.

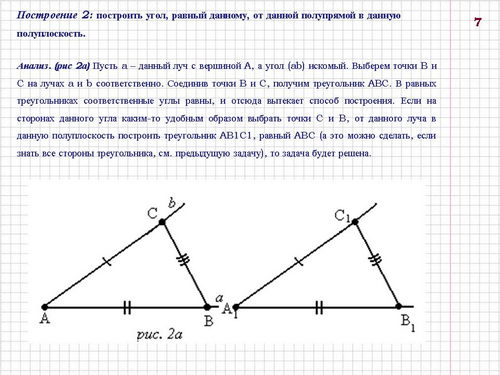
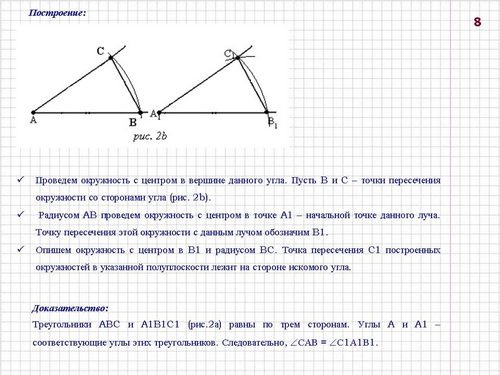
Построение 2: построить угол, равный данному, от данной полупрямой в данную полуплоскость (слайды 7-8).

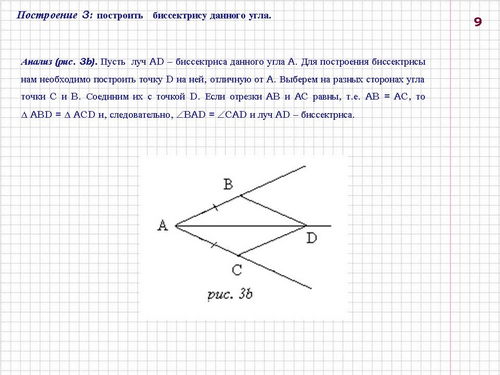
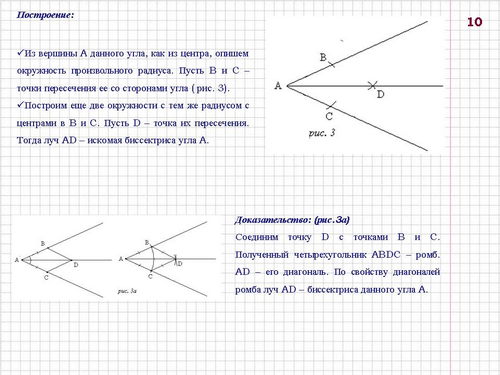
Построение 3: построить биссектрису данного угла (слайды 9-10).

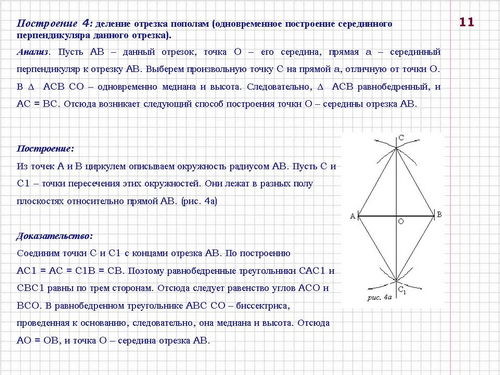
Построение 4: деление отрезка пополам (одновременное построение серединного перпендикуляра данного отрезка) (слайд 11).

Построение 5:  через точку O провести прямую, перпендикулярную данной прямой a. Рассмотреть два возможных случая (слайды 12-14).

Построение 6: построение прямой, проходящей через данную точку А параллельно данной прямой а. (слайд 15).

4. Решение задач на построение;

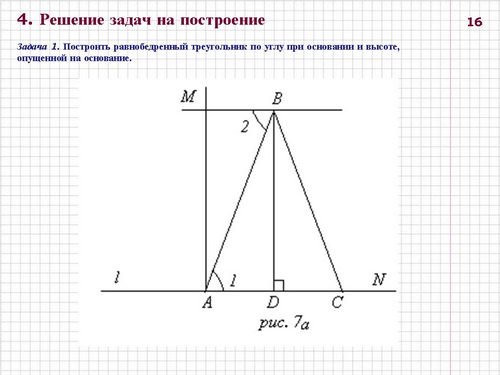
Задача 1. Построить равнобедренный треугольник по углу при основании и высоте, опущенной на основание (слайд 16).

Анализ. ( рис. 1) Предположим, что задача решена, и построен равнобедренный треугольник АВС, АВ = ВС, в котором угол ВАС = a и высота BD = отрезку h.

В равнобедренном треугольнике высота BD, проведенная к основанию, является медианой, поэтому AD = DC. Значит, сначала необходимо построить прямоугольный треугольник ABD. Для этого строим угол А, равный углу a , затем нужно найти точку В, лежащую на одной из сторон угла на расстоянии h от другой стороны. Точку В можно получить как пересечение стороны угла и прямой, параллельной другой стороне и проходящей от нее на расстоянии h.

Построение (рис. 2):

Проводим прямую l, выбираем точку А, на луче AN откладываем угол 1, равный данному углу a . (используем построение 2)

Через точку А проводим прямую, перпендикулярную прямой AN (построение 5), и на построенной прямой откладываем отрезок АМ = h (в той же полуплоскости, в которой построен угол).

Через точку М проводим прямую, параллельную прямой AN (построение 6), точку ее пересечения со стороной угла обозначаем В.

Из точки В опускаем перпендикуляр BD на прямую AN (построение 5) и откладываем DC = DA. Соединяем В и С.

Доказательство: Треугольник АВС - искомый, т.к. он удовлетворяет всем условиям задачи. Действительно, по построению МВ || AD, поэтому 1 = 2; по построению АМ AD, МВ || AD, следовательно, АМ МВ. В прямоугольных треугольниках ABD и ВАМ общая гипотенуза АВ и равные углы 1 и 2, эти треугольники равны, значит BD = AM, т.е. BD = h. Далее, по построению DC = DA, поэтому  ABD =  СВD (по двум катетам), откуда следует, что С = А = a и BD = h.

Исследование: В равнобедренном треугольнике угол при основании острый, поэтому построение возможно, если заданный угол острый.

Построение единственно, т.к. точка В находится единственным образом. Задача имеет только одно решение.

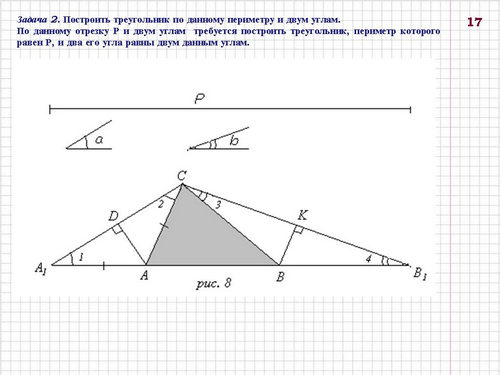
Задача 2. Построить треугольник по данному периметру и двум углам (слайд 17).

Анализ (рис. 3) Предположим, что такой треугольник АВС построен.

АВ +ВС + АС = Р, А = a , В = . На прямой АВ отложим отрезки АА₁= АС и ВВ₁ = ВС, тогда А₁В₁ = Р. Треугольник А₁АС равнобедренный, 1 = 2, а по теореме о внешнем угле треугольника ВАС = 1 + 2. Таким образом, 1 = 2 = a /2.

Аналогично 3 = 4 = /2. В треугольнике А₁В₁С известны два угла 1 и 3 и сторона между ними А₁В₁ = Р. Такой треугольник можно построить, тогда точки А и В найдутся, как точки пересечения серединных перпендикуляров отрезков А₁С и В₁С с прямой А₁В₁.

Построение: Делим данные углы a и пополам (построение 3).

1. Проводим произвольную прямую и на ней откладываем отрезок А₁В₁, равный отрезку Р. От луча А₁В₁ откладываем угол 1, равный a /2, а от луча В₁А₁ в ту же полуплоскость откладываем угол 3, равный 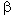/2 (построение 2), точку пересечения сторон этих углов обозначим С.
2. Строим серединные перпендикуляры отрезков А₁С и В₁С (построение 4), точки их пересечения с прямой А₁В₁ обозначим А и В. Соединяем точки А и В с точкой С. Треугольник АВС - искомый.

Доказательство: По построению А₁D = DC, AD А₁С, следовательно, А₁АD = CAD (по первому признаку) и А₁А = АС.

Аналогично КВ В₁С, В₁К = КС, поэтому ВВ₁ = ВС и АС + АВ +ВС = АА₁ + АВ + ВВ₁ = Р. Кроме того, САВ = 3 + 4 = b .

Исследование: Построение возможно всегда, если только сумма двух углов меньше 180° (сумма двух углов треугольника всегда меньше 180° ). Решение единственно, т.к. точка С, а затем точки А и В определяются единственным образом.

Замечание: В этой задаче была задана сумма сторон треугольника, при решении как бы "развернули" стороны треугольника, пока они не легли на одну прямую - получили отрезок А₁В₁, равный данному. Этот прием называют методом спрямления и применяют в задачах, в которых задана сумма (либо разность) сторон треугольника.

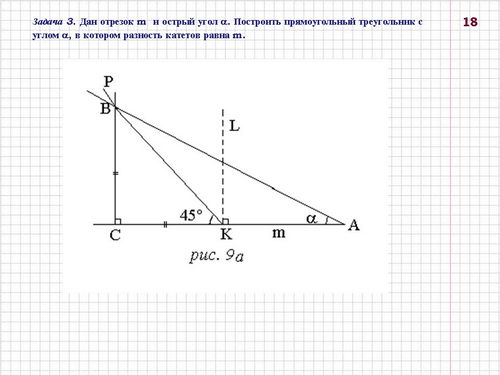
Задача 3. Дан отрезок m и острый угол a . Построить прямоугольный треугольник с углом a, в котором разность катетов равна m (слайд18).

Анализ (рис. 4): Предположим, что построен прямоугольный треугольник АВС с углом А, равным a, и разностью катетов, равной m.

Применим метод спрямления: отложим на прямой АС от точки С отрезок СК, равный ВС, тогда АК = m. В треугольнике АКВ известна сторона АК и два прилежащих угла: ВАК = a и ВКА = 135°. Такой треугольник можно построить, а точку С найти как основание перпендикуляра из точки В на прямую АК.

Построение (рис. 5) :

На прямой l выбираем точку А и откладываем отрезок АК = m. Через точку К проводим перпендикуляр KL к прямой АК (построение 5).

Проводим биссектрису КР угла, дополнительного к прямому углу АКL (построение 3).

От луча АК откладываем угол КАМ, равный данному углу a (построение 2), точку пересечения с прямой КР обозначаем В.

Из точки В опускаем перпендикуляр ВС на прямую АК (построение 5). Треугольник АВС - искомый.

Доказательство: А = a , C=90° , ВКС=45° (по построению), следовательно, ВС = СК и АС = ВС = АС - СК = АК = m.

Исследование: Указанное построение выполнимо, если прямая АМ пересекает биссектрису КР прямого угла, т.е. если a < 45° . В рассматриваемом случае катет АС больше катета ВС, значит, угол a меньше 45° .

Если задан угол a < 45°, то описанное построение решает задачу. Если задан угол a , 45° < a < 90° , то выполняем аналогичное построение для угла a ' = 90° - a . Треугольник определен однозначно.

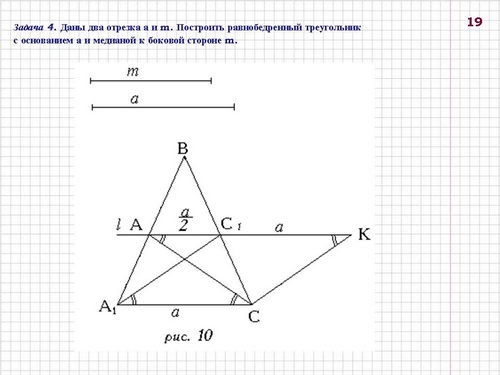
Задача 4. Даны два отрезка а и m. Построить равнобедренный треугольник с основанием а и медианой к боковой стороне m (слайд 19).

Анализ (рис.6): Предположим, что построен равнобедренный треугольник АВС, АВ = ВС, в котором АС = а, АС₁ = СА₁ = m. Точки А₁ и С₁ - середины боковых сторон, А₁С₁ - средняя линия А₁С₁ || АС и А₁С₁ = .

Продлим отрезок А₁С₁ и на прямой А₁С₁ отложим отрезок С₁К = а. Тогда АС₁КС - параллелограмм, а треугольник А₁СК - равнобедренный: СА₁ = СК = m. Этот треугольник можно построить.

Построение:

Делим данный отрезок а пополам (построение 4).

На прямой l выбираем точку К и откладываем последовательно два отрезка КС₁ = а и С₁А₁ = . В нижнюю полуплоскость строим треугольник А₁СК по трем сторонам (построение 1).

Через точку С проводим прямую, параллельную прямой l (построение 6) и на ней откладываем отрезок СА = а. Проводим прямые АА₁ и СС₁, получаем точку В. Треугольник АВС - искомый.

Доказательство: В построенном треугольнике АВС отрезок А₁С₁ = АС и А₁С₁ || АС, значит А₁С₁ - средняя линия и точки А₁ и С₁ - середины сторон АВ и СВ, а отрезки СА₁ и АС₁ - медианы. По построению СА₁ = m, а из параллелограмма АС₁КС следует, что и АС₁ = m.

Расставим равные углы в треугольнике А₁СК и в параллелограмме АС₁КС. Теперь заметим, что С₁АС = А₁СА (по двум сторонам а и m и углу между ними). Следовательно, С₁С = А₁А и СВ = АВ - треугольник равнобедренный.

Исследование: Построение возможно, если существует треугольник А₁КС со сторонами А₁С = СК = m и А₁К =а, что возможно лишь при условии а < 2m, т.е. при m > . Построение единственно, все точки определяются единственным образом.

5. Задачи для самостоятельного решения

Задача 1. Через данную точку провести прямую под данным углом к данной прямой (слайд 20).

Указание к решению задачи: Построить угол, равный данному в произвольной точке данной прямой, одна из сторон которого лежит на этой прямой; затем через данную точку провести параллельную прямую.

Задача 2. описать окружность, которая проходила бы через данную точку А и касалась бы данной прямой в данной на ней точке В (слайд 21).

Указание к решению задачи: К данной прямой восстановить перпендикуляр из данной точки В, построить серединный перпендикуляр к отрезку АВ (А - другая данная точка). Их пересечение - точка О - центр искомой окружности, ОВ - радиус.

Задача 3. Провести в треугольнике прямую, параллельную основанию так, чтобы отрезок, заключенный между боковыми сторонами был равен сумме отрезков боковых сторон, считая от основания (слайд 22).

Указание к решению задачи (слайд):Через точку пересечения биссектрис провести прямую MN, параллельную основанию. Получим равнобедренные треугольники ONC и ОМА (теорема о накрест лежащих углах при параллельных прямых, свойства сторон и углов в равнобедренном треугольнике).

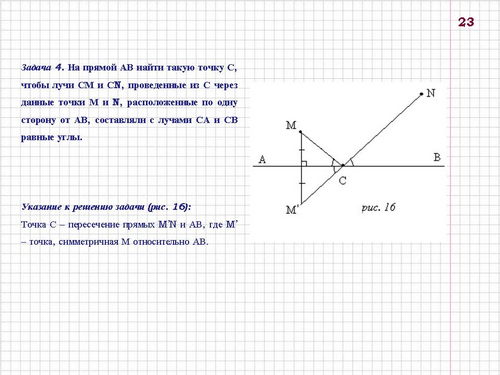
Задача 4. На прямой АВ найти такую точку С, чтобы лучи СМ и СN, проведенные из С через данные точки М и N, расположенные по одну сторону от АВ, составляли с лучами СА и СВ равные углы (слайд 23).

Указание к решению задачи (рис. 16): Точка С - пересечение прямых M'N и АВ, где M' - точка, симметричная М относительно АВ.

6. Список литературы (слайд 24).