Рекомендации по решению нетрадиционных задач на расчет электрических цепей постоянного тока

Введение

Решение задач - неотъемлемая часть обучения физике, поскольку в процессе решения задач происходит формирование и обогащение физических понятий, развивается физическое мышление учащихся и совершенствуется их навыки применения знаний на практике.

В ходе решения задач могут быть поставлены и успешно реализованы следующие дидактические цели:

• Выдвижение проблемы и создание проблемной ситуации;
• Обобщение новых сведений;
• Формирование практических умений и навыков;
• Проверка глубины и прочности знаний;
• Закрепление, обобщение и повторение материала;
• Реализация принципа политехнизма;
• Развитие творческих способностей учащихся.

Наряду с этим при решении задач у школьников воспитываются трудолюбие, пытливость ума, смекалка, самостоятельность в суждениях, интерес к учению, воля и характер, упорство в достижении поставленной цели. Для реализации перечисленных целей особенно удобно использовать нетрадиционные задачи.

§1. Задачи по расчету электрических цепей постоянного тока

По школьной программе на рассмотрение данной темы очень мало отводится времени, поэтому учащиеся более или менее успешно овладевают методами решения задач данного типа. Но часто такие типы задач встречаются олимпиадных заданиях, но базируются они на школьном курсе.

К таким, нестандартным задачам по расчету электрических цепей постоянного тока можно отнести задачи, схемы которых:

1) содержат большое число элементов – резисторов или конденсаторов;

2) симметричны;

3) состоят из сложных смешанных соединений элементов.

В общем случае всякую цепь можно рассчитать, используя законы Кирхгофа. Однако эти законы не входят в школьную программу. К тому же, правильно решить систему из большого числа уравнений со многими неизвестными под силу не многим учащимся и этот путь не является лучшим способом тратить время. Поэтому нужно уметь пользоваться методами, позволяющими быстро найти сопротивления и емкости контуров.

§2. Метод эквивалентных схем

Метод эквивалентных схем заключается в том, что исходную схему надо представить в виде последовательных участков, на каждом из которых соединение элементов схемы либо последовательно, либо параллельно. Для такого представления схему необходимо упростить. Под упрощением схемы будем понимать соединение или разъединение каких-либо узлов схемы, удаление или добавление резисторов, конденсаторов, добиваясь того, чтобы новая схема из последовательно и параллельно соединенных элементов была эквивалентна исходной.

Эквивалентная схема – это такая схема, что при подаче одинаковых напряжений на исходную и преобразованную схемы, ток в обеих цепях будет одинаков на соответствующих участках. В этом случае все расчеты производятся с преобразованной схемой.

Чтобы начертить эквивалентную схему для цепи со сложным смешанным соединением резисторов можно воспользоваться несколькими приемами. Мы ограничимся рассмотрением в подробностях лишь одного из них – способа эквипотенциальных узлов.

Этот способ заключается в том, что в симметричных схемах отыскиваются точки с равными потенциалами. Эти узлы соединяются между собой, причем, если между этими точками был включен какой-то участок схемы, то его отбрасывают, так как из-за равенства потенциалов на концах ток по нему не течет и этот участок никак не влияет на общее сопротивление схемы.

Таким образом, замена нескольких узлов равных потенциалов приводит к более простой эквивалентной схеме. Но иногда бывает целесообразнее обратная замена одного узла

несколькими узлами с равными потенциалами, что не нарушает электрических условий в остальной части.

Рассмотрим примеры решения задач эти методом.

З а д а ч а №1

Рассчитать сопротивление между точками А и В данного участка цепи. Все резисторы одинаковы и их сопротивления равны r.

Решение:

В силу симметричности ветвей цепи точки С И Д являются эквипотенциальными. Поэтому резистор между ними мы можем исключить. Эквипотенциальные точки С и Д соединяем в один узел. Получаем очень простую эквивалентную схему:

Сопротивление которой равно:

RАВ=Rac+Rcd=r*r/r*r+r*r/r+r=r.

З а д а ч а № 2

Решение:

В точках F и F` потенциалы равны, значит сопротивление между ними можно отбросить. Эквивалентная схема выглядит так:

Сопротивления участков DNB;F`C`D`; D`, N`, B`; FCD равны между собой и равны R1:

1/R1=1/2r+1/r=3/2r

R1=2/3*r

С учетом этого получается новая эквивалентная схема:

Ее сопротивление и сопротивление исходной цепи RАВ равно:

1/RАВ=1/r+R1+R1+1/r+R1+R1=6/7r

RАВ=(7/6)*r.

З а д а ч а № 3.

Решение:

Точки С и Д имеют равные потенциалы. Исключением сопротивление между ними. Получаем эквивалентную схему:

Искомое сопротивление RАВ равно:

1/RАВ=1/2r+1/2r+1/r=2/r

RАВ=r/2.

З а д а ч а № 4.

Решение:

Как видно из схемы узлы 1,2,3 имеют равные потенциалы. Соединим их в узел 1. Узлы 4,5,6 имеют тоже равные потенциалы- соединим их в узел 2. Получим такую эквивалентную схему:

Сопротивление на участке А-1, R 1-равно сопротивлению на участке 2-В,R3 и равно:

R1=R3=r/3

Сопротивление на участке 1-2 равно: R2=r/6.

Теперь получается эквивалентная схема:

Общее сопротивление RАВ равно:

RАВ= R1+ R2+ R3=(5/6)*r.

З а д а ч а № 5.

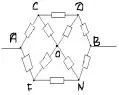
Решение:

Точки C и F-эквивалентные. Соединим их в один узел. Тогда эквивалентная схема будет иметь следующий вид:

Сопротивление на участке АС:

Rас=r/2

Сопротивление на участке FN:

R_FN =

Сопротивление на участке DB:

R_DB =r/2

Получается эквивалентная схема:

Искомое общее сопротивление равно:

R_AB= r.

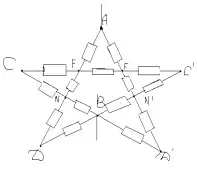
Задача №6

Решение:

Заменим общий узел О тремя узлами с равными потенциалами О, О₁ , О₂. Получим эквивалентную систему:

Сопротивление на участке ABCD:

R₁=(3/2)*r

Сопротивление на участке A`B`C`D`:

R₂= (8/3)*r

Сопротивление на участке ACВ

R₃ = 2r.

Получаем эквивалентную схему:

Искомое общее сопротивление цепи R_AB равно:

R_AB= (8/10)*r.

Задача №7.

Решение:

“Разделим” узел О на два эквипотенциальных угла О₁ и О₂. Теперь схему можно представить, как параллельные соединение двух одинаковых цепей. Поэтому достаточно подробно рассмотреть одну из них:

Сопротивление этой схемы R₁ равно:

R₁ = 3r

Тогда сопротивление всей цепи будет равно:

R_AB = (3/2)*r

З а д а ч а №8

Решение:

Узлы 1 и 2 – эквипотенциальные, поэтому соединим их в один узел I. Узлы 3 и 4 также эквипотенциальные – соединимих в другой узел II. Эквивалентная схема имеет вид:

Сопротивление на участке A- I равно сопротивлению на участке B- II и равно:

R_I =

Сопротивление участка I-5-6- II равно:

R_II = 2r

Cопротивление участка I- II равно:

R_III =

Получаем окончательную эквивалентную схему:

Искомое общее сопротивление цепи R_AB=(7/12)*r.

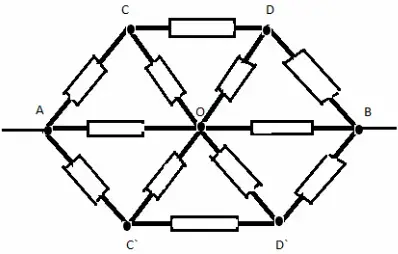
З а д а ч а №9

В ветви ОС заменим сопротивление на два параллельно соединенных сопротивления по 2r. Теперь узел С можно разделить на 2 эквипотенциальных узла С₁ и С₂. Эквивалентная схема в этом случае выглядит так:

Сопротивление на участках ОС_IB и DC_IIB одинаковы и равны, как легко подсчитать 2r. Опять чертим соответствующую эквивалентную схему:

Сопротивление на участке AOB равно сопротивлению на участке ADB и равно (7/4)*r. Таким образом получаем окончательную эквивалентную схему из трех параллельно соединенных сопротивлений:

Ее общее сопротивление равно R_AB= (7/15)*r

З а д а ч а № 10

Точки СОD имеют равные потенциалы – соединим их в один узел О^I .Эквивалентная схема изображена на рисунке :

Сопротивление на участке А О^I равно . На участке О^IВ сопротивление равно .Получаем совсем простую эквивалентную схему:

ЕЕ сопротивление равно искомому общему сопротивлению

R_AB=(5/6)*r

Задачи № 11 и № 12 решаются несколько иным способом, чем предыдущие. В задаче №11 для ее решения используется особое свойство бесконечных цепей, а в задаче № 12 применяется способ упрощения цепи.

Задача № 11

Решение

Выделим в этой цепи бесконечно повторяющееся звено, оно состоит в данном случае из трех первых сопротивлений. Если мы отбросим это звено, то полное сопротивление бесконечной цепи R не измениться от этого , так как получится точно такая же бесконечная цепь. Так же ничего не измениться, если мы выделенное звено подключим обратно к бесконечному сопротивлению R, но при этом следует обратить внимание , что часть звена и бесконечная цепь сопротивлением R соединены параллельно. Таким образом получаем эквивалентную схему :

Получается уравнения

R_AB=2ч +

R_AB = R

Решая систему этих уравнений, получаем:

R=ч (1+ ).

§3. Обучение решению задач по расчету электрических цепей способом эквипотенциальных узлов

Задача – это проблема, для разрешения которой ученику потребуются логические рассуждения и выводы. Строящиеся на основе законов и методов физики. Таким образом, с помощью задач происходит активизация целенаправленного мышления учащихся.

В то же время. Теоретические знания можно считать усвоенными только тогда, когда они удачно применяются на практике. Задачи по физике описывают часто встречающиеся в жизни и на производстве проблемы, которые могут быть решены с помощью законов физики и, если ученик успешно решает задачи, то можно сказать, что он хорошо знает физику.

Для того, чтобы ученики успешно решали задачи, недостаточно иметь набор методов и способов решения задач, необходимо еще специально учить школьников применению этих способов.

Рассмотрим план решения задач по расчету электрических цепей постоянного тока методом эквипотенциальных узлов.

1. Чтение условия.
2. Краткая запись условия.
3. Перевод в единицы СИ.
4. Анализ схемы:
1. установить, является ли схема симметричной;
2. установить точки равного потенциала;
3. выбрать, что целесообразнее сделать – соединить точки равных потенциалов или же, наоборот, разделить одну точку на несколько точек равных потенциалов;
4. начертить эквивалентную схему;
5. найти участки только с последовательным или только с параллельным соединением и рассчитать общее сопротивление на каждом участке по законам последовательного и параллельного соединения;
6. начертить эквивалентную схему, заменяя участки соответствующими им расчетными сопротивлениями;
7. пункты 5 и 6 повторять до тех пор, пока не останется одно сопротивление, величина которого и будет решением задачи.
5. Анализ реальности ответа.

Подробнее об анализе схемы

а) установить, является ли схема симметричной.

Определение. Схема симметрична, если одна ее половина является зеркальным отражением другой. Причем симметрия должна быть не только геометрической, но должны быть симметричны и численные значения сопротивлений или конденсаторов.

Примеры:

1)

Схема симметричная, так как ветви АСВ и АДВ симметричны геометрически и отношение сопротивления на одном участке АС:АД=1:1 такое же, как и на другом участке СД:ДВ=1:1.

2)

Схема симметричная, так как отношение сопротивлений на участке АС:АД=1:1 такое же, как и на другом участке СВ:ДВ=3:3=1:1

3)

Схема не симметрична, так как отношения сопротивлений численно

не симметричны -1:2 и 1:1.

б) установить точки равных потенциалов.

Пример:

Из соображений симметрии делаем вывод, что в симметричных точках потенциалы равны. В данном случае симметричными точками являются точки С и Д. Таким образом, точки С и Д – эквипотенциальные точки.

в) выбрать, что целесообразно сделать – соединить точки равных потенциалов или же, наоборот, разделить одну точку на несколько точек равных потенциалов.

Мы видим в этом примере, что между точками равных потенциалов С и Д включено сопротивление, по которому ток не будет течь. Следовательно, мы можем отбросить это сопротивление, а точки С и Д соединить в один узел.

г) начертить эквивалентную схему.

Чертим эквивалентную схему. При этом получаем схему с соединенными в одну точку точками С и Д.

д) найти участки только с последовательным или только с параллельным соединением и рассчитать общее сопротивление на каждом таком участке по законам последовательного и параллельного соединения.

Из полученной эквивалентной схемы видно, что на участке АС мы имеем два параллельно соединенных резистора. Их общее сопротивление находится по закону параллельного соединения:

1/ Rобщ=1/R1+1/R2+1/R3+…

Таким образом 1/RAC=1/r+1/r=2/r,откуда RAC= r/2.

На участке СВ картина аналогичная:

1/RCB= 1/r+1/r =2/r, откуда RCB=r/2.

е)начертить эквивалентную схему, заменяя участки соответствующими им расчетными сопротивлениями.

Чертим эквивалентную схему подставляя в нее рассчитанные сопротивления участков RAC и RCB:

ж)пункты д) и е) повторять до тех пор, пока останется одно сопротивление, величина которого и будет решением задачи.

Повторяем пункт д): на участке АВ имеем два последовательно соединенных сопротивления. Их общее сопротивление находим по закону последовательного соединения:

Rобщ= R1+R2+R3+… то есть, RAB=RAC+RCB = r/2+r/2 =2r/2 = r.

Повторяем пункт е): чертим эквивалентную схему:

Мы получили схему с одним сопротивлением, величина которого равна сопротивлению исходной схемы. Таким образом, мы получили ответ RAB = r.

Далее, для проверки усвоения данного материала можно учащимся предложить задания для самостоятельной работы, взятые из дидактического материала. (см. приложение)

Литература

1. Балаш. В.А. задачи по физике и методы их решения. - М: Просвещение,1983.
2. Лукашик В.И. Физическая олимпиада.- М: Просвещение, 2007
3. Усова А.В., Бобров А.А. Формирование учебных умений и навыков учащихся на уроках физики.- М: Просвещение,1988
4. Хацет А. Методы расчета эквивалентных схем //Квант.
5. Чертов А. Г. Задачник по физике. – М.: Высшая школа,1983
6. Зиятдинов Ш.Г., Соловьянюк С.Г. (методические рекомендации) г. Бирск,1994г
7. Марон А.Е., Марон Е.А. Физика. Дидактические материалы. Москва, “Дрофа”, 2004г