В условиях высокого уровня развития науки и техники особые требования предъявляются к подготовке учащихся в школе. Задача образования не может сводиться только к вооружению учащихся определенной суммой знаний. Необходимо сформировать у них умение оперировать приобретенными знаниями, применять их в новых ситуациях, делать самостоятельные выводы и обобщения, находить решения в нестандартных условиях. В настоящий период, когда развитие науки и техники происходит чрезвычайно быстро, когда делаются все новые и новые научные открытия, когда появляются неизвестные ранее отрасли науки, техники, экономики, исключительную значимость приобретает проблема подготовки учащихся к овладению новыми знаниями, к изучению научной и технической литературы.
Предлагаемая тема посвящена одному их основных понятий современной математики – функциональной зависимости. Понятие функциональной зависимости, являясь одним из центральных в математике, пронизывает все ее приложения, оно, как ни одно другое, приучает воспринимать величины в их живой изменчивости, во взаимной связи и обусловленности. Изучение поведения функций, их свойств, построение их графиков и применения для решения прикладных задач является важным разделом школьного курса.
Существуют различные способы задания функции: аналитический, табличный, словесный, а также графический. Иногда график является единственно возможным способом задания функции. Он широко используется в технике, лежит в основе работы многих самопишущих автоматических приборов. Свободное владение техникой построения графиков часто помогает решать сложные задачи, а порой является единственным средством их решения. Однако на базе основной школы материал, связанный с этим вопросом, представлен несколько хаотично, изучается недостаточно полно, многие важные моменты не входят в программу и, следовательно, не изучаются.
Материал предоставленной презентации содержит нестандартные методы, которые позволяют более эффективно решать различные задачи. К нестандартным задачам традиционно относятся задачи, которые выделяются необычной формулировкой, а также задачи, для решения которых требуются умения нестандартно мыслить, переносить известные методы решения в непривычные ситуации, проявлять находчивость и сообразительность, способствуют развитию логического мышления, математической интуиции, творческих способностей, прививает навыки исследовательской работы.
Наряду с основной задачей обучения математике – обеспечение прочного и сознательного овладения учащимися системой математических знаний и умений – тема «Методика исследования функций и построение графиков функций» предусматривает формирование устойчивого интереса к предмету, развитие математических способностей.
В рамках содержательной линии решаются следующие задачи:
- расширение и систематизация общих сведений о функциях;
- пополнение класса изучаемых функций;
- иллюстрация широты применения функций для описания и изучения реальных зависимостей.
Умение с помощью графика «прочитать» поведение функции на некотором промежутке находит применение в любой практической деятельности человека, в которой ему приходится иметь дело с теми или иными графическими изображениями зависимостей. Кроме того, умение строить графики функций представляет большой самостоятельный интерес.
Само понятие функциональной зависимости отражает объективные закономерности природы. Данное понятие является основным во всей высшей математике и поэтомуобъяснение его в средней школе – важная предпосылка к усвоению курса высшей математики.
Функция определяется как соответствие между значениями двух переменных величин. Исторически первым способом задания функции был способ аналитический – при помощи формулы. Аналитический способ задания функции оказался удобным средством исследования, функцию стали отождествлять с ее аналитическим выражением. Возникла необходимость освободить понятие функции от теснящих ее рамок формулы. Это «освобождение» было сделано в первой половине прошлого столетия: было дано определение функции, в котором нет никакого упоминания не только об аналитическом выражении, но и вообще о способе установления соответствия.
Из определения функции следует, что для ее задания необходимо указать два множества чисел (значений аргумента и функции) и закон соответствия между ними. Это можно сделать четырьмя способами: таблицей, аналитически (формулой), графически и словесно.
В настоящее время некоторые функции изучают по
графикам этих функций.
Например: сейсмолог, анализируя сейсмограмму,
узнает, когда было землетрясение, где оно
произошло, определяет силу и характер
толчков. Врач, исследующий больного, может по
кардиограмме судить о нарушениях сердечной
деятельности; изучение кардиограммы помогает
правильно поставить диагноз заболевания;
инженер-радиоэлектроник по характеристике
полупроводникового элемента выбирает
наиболее подходящий режим его работы.
В школе изучают числовые функции –
функции, определенные на множестве
действительных чисел и принимающие значения
также на множестве действительных чисел.
Функциональная зависимость y = f(x)
задается в явном виде (аналитическим выражением).
Например, y = x2, y = x3,
, y = sin x и
т.д. Первая, вторая и четвертая функции
определены на множестве всех действительных R,
а третья – на множестве всех
неотрицательных чисел R. Определение
функции требует, чтобы каждому значению
аргумента x из области
определения функции отвечало одно
единственное значение y .
Например, график,
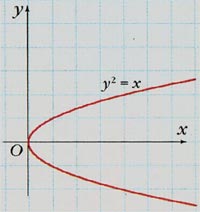
не определяет никакой функции.
На рисунке
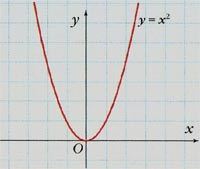
изображен график функции, одно и то же значение y из множества Y, которой, соответствует нескольким или не соответствует ни одному из возможных значений аргумента x.
Если функция f такова, что каждое y из множества Y сопоставлено одному единственному элементу x из множества X (y = f(x)), то на множестве Y можно определить функцию f ', такую, что x = f'(y). Эта функция называется обратной функцией f.
Для функции y = x3, заданной на
множестве R, обратной будет функция x
= 
, а для
функции на
множестве R+ – функция x
= y2. Поскольку аргумент
функции все же принято обозначать через x,
то, например, вместо x = y3 пишут
y = .
Итак, функция y = x3 и y = – обратные
друг другу на R, а функции y = x2 и
– обратные
друг другу на R+.
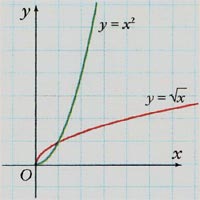
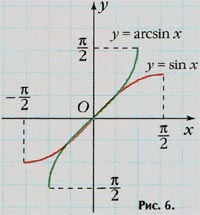
Если функцию рассматривать лишь на
отрезке X = 
, а в качестве множества Y
взять отрезок [– 1; 1], то обратной ей будет функция
y = arcsin x
Особую роль при изучении алгебры играет функциональная линия. Наличие прочной функциональной основы позволит учащимся осмыслить большой класс явлений, встречающихся в теории и практике. Систематическое использование функциональной линии позволит увидеть связь между понятиями.
Различные подходы к определению понятия функция
Введение понятия «функция» в школьный курс математики позволил выделить четыре основные проблемы, вокруг которых существовали расхождения во мнениях методистов, а именно:
- цель и значение изучения понятия функции учащимися;
- подходы к определению функции;
- вопрос функциональной пропедевтики;
- место и объем функционального материала в курсе школьной математики.
Несмотря на чрезвычайно большой объем, широту и сложность понятия функции, его простейший вариант дается уже в средних классах школы. Это понятие в дальнейшем играет важную роль, являясь базовым понятием в изучении алгебры и начал анализа. Начиная с 7 класса средней школы идет постепенное изучение свойств функций и функциональных зависимостей. Рассматриваются различные классы функций: начиная с простейших линейных функций и их графиков, затем следуют квадратичные функции, функции обратной пропорциональности и дробно-линейные функции. В старших классах вводятся тригонометрические функции, и, наконец, показательные и логарифмические функции. Все эти функции рассматриваются только как функции одной переменной, причем сами переменные не выходят за рамки множества вещественных чисел.
Введение понятия функции – длительный процесс, завершающийся формированием представлений обо всех компонентах этого понятия в их взаимной связи и о роли, играемой им в математике и в ее приложениях. Этот процесс ведется по трем основным направлениям:
- упорядочение имеющихся представлений о функции, развертывание системы понятий, характерных для функциональной линии (способы задания и общие свойства функций, графическое истолкование области определения, области значений, возрастания и т. д. на основе метода координат);
- глубокое изучение отдельных функций и их классов;
- расширение области приложений алгебры за счет включения в нее идеи функции и разветвленной системы действий с функцией.
Первое из этих направлений проявляется в курсе школьной алгебры ранее остальных.
В реализации этого направления значительное место отводится усвоению важного представления, входящего в понятие функции,– однозначности соответствия аргумента и определенного по нему значения функции. Для рассмотрения этого вопроса привлекаются различные способы задания функции.
Чаще других в математике и ее приложениях применяется задание функции формулой. Все другие способы играют подчиненную роль. Именно поэтому после первого знакомства с несколькими такими способами основное внимание в обучении уделяется тем функциям и классам, которые имеют стандартную алгебраическую форму их выражения. Однако при введении понятия сопоставление разных способов задания функции выполняет важную роль. Во-первых, оно связано с практической потребностью: и таблицы, и графики, как правило, служат для удобного в определенных обстоятельствах представления функции, имеющей аналитическую форму записи. Во-вторых, оно важно для усвоения всего многообразия аспектов понятия функции. Формула выражает функцию лишь, будучи включенной в соответствующую систему представлений и операций, а эта система такова, что различные компоненты понятия функции могут быть отображены наиболее естественно различными средствами.
Использование перевода задания функции из одной формы представления в другую – необходимый методический прием при введении понятия функции.
Реализация этого приема состоит в использовании системы заданий, в которых представлены все случаи такого перевода. Если ограничиться основными способами представления функции – формулой, графиком, таблицей, то получится 6 типов упражнений, при которых форма представления меняется, и 3 – при которых она остается такой же.
В настоящее время в изучении понятия функции в школе преобладающими являются два основных подхода: индуктивный и дедуктивный. Сложившись исторически, они наиболее полно отвечают целям и задачам образования, и поэтому именно им отдано предпочтение при изучении математики, в том числе функций, в средних классах школ.
Используя опыт практического преподавания можно сделать следующие выводы:
1. Графики функций являются наиболее удобным и
наглядным средством для обучения учащихся
исследованию функций.
2. Преподавание темы «Методика исследования
функций и построение их графиков» требует
тщательного подбора содержания средств и
методов обучения, то есть разработки эффективной
методики.
В результате систематизируются знания учащихся о функциях, их свойствах, которые складываются постепенно. Эти знания важны для того, чтобы достойно сдать экзамены и для дальнейшего обучения. Умение использовать исследование функции для построения графиков играет немаловажную роль для решения нестандартных задач повышенной трудности, таких как: решение уравнений с параметрами; решение уравнений, содержащих модули; решение неравенств, содержащих параметры и т.д.
Приобретаемые навыки работы с формулой, аппарат исследования основных элементарных функций необходимы для изучения электродинамики и оптики. Элементы дифференциального исчисления находят применения при изучении явления радиоактивного распада, гармонических колебаний. Существенную роль играют навыки построения графиков функции при изучении физики.
На основе этих знаний у учащихся формируются общепредметные расчетно-измерительные умения. Изучение этого материала опирается на межпредметные связи с курсами черчения, физической географии, трудового обучения.