Цели. Создать условия для установления учащимися причинно-следственных связей потери и появления корней при решении логарифмических уравнений, развитие осознанного отношения учащихся к понятиям “равносильность”, “равносильный переход”, “ОДЗ уравнения”, развитие у них потребности избегать при решении логарифмических уравнений формального использования логарифмических формул, развитие теоретической грамотности учащихся, аналитических умений, познавательной активности, развитие творческих способностей.
Ход урока
I. Организация урока
II. Организация проблемной ситуации, по логике поиска решения которой возникают дополнительные проблемы (выявленные учащимися и предусмотренные при конструировании ситуации)
1) Организация учебной ситуации, в которой учащимся требуется понять и сформулировать имеющуюся в ней проблему.
Проверка домашнего задания. Решить уравнения:
Проверку корней учащиеся выполняли путем
непосредственной подстановки получившихся
чисел в заданные уравнения, что позволило им
выявить посторонний корень уравнения 
Это
Учащимся
предлагается проверить, является ли число 
корнем
уравнения 
который ими был потерян.
Так возникла проблема: “Каковы причины потери и приобретения посторонних корней при решении логарифмических уравнений?”.
Если при изучении темы “Равносильные уравнения” не акцентировалось внимание на причинах потери и приобретения корней, то выдвинутая учащимися проблема выглядит вполне естественно. В процессе ее обсуждения учащиеся предполагают, что связано это с выполняемыми преобразованиями.
2) Организация решения проблемы.
а) выбор учащимися сведений, связанных с данной проблемой - понятий равносильных уравнений, равносильных на множестве уравнений, уравнений-следствий, равносильного перехода, ОДЗ уравнения;
б) проверка учащимися равносильности уравнений
и 
, уравнений 
и 
;
в) проверка равносильности переходов от
исходных уравнений к уравнениям 
;
Итогом работы должен стать ответ на вопрос: “Каковы
причины потери и приобретения посторонних
корней при решении логарифмических уравнений?”.
Ответ учащихся может быть таким: “При решении
уравнений выполняются неравносильные
переходы”.
3) В процессе поиска решения учащиеся приходят к новой проблеме: “Как избежать неравносильных переходов?”.
Групповая работа.
Задания для групп.
– Покажите, что уравнения 
являются равносильными на
множестве 
.
(Ответ: на данном интервале они имеют один и тот
же корень 
).
– Покажите, что уравнения
являются равносильными на
множестве 
.(Ответ:
первое уравнение, как было установлено, имеет два
корня -
и 
, но данному
интервалу принадлежит только один корень, равный
5; второе уравнение имеет всего один корень - 
, и он
удовлетворяет интервалу 
).
Итогом работы должен стать ответ на вопрос: “Как избежать неравносильных переходов?”. Ответ может быть таким: “Все переходы надо выполнять на некотором общем множестве”.
4) Формулируется следующая проблема: “На каком множестве следует выполнять равносильные переходы?”
Групповая работа
Задание для групп
1) Найдите ОДЗ уравнений: 
и 
.
Проследите, как изменяется ОДЗ при переходе от
первого уравнения ко второму уравнению,
попытайтесь сделать соответствующий вывод.
Сформулируйте ответ на вопрос: “На каком
множестве следует выполнять равносильные
переходы при решении уравнений?”
Ответ. ОДЗ первого уравнения определяется системой
двух неравенств 
и 
.
Решение системы неравенств: 
.
ОДЗ уравнения определяется условием 
. Решение этого
неравенства: 
и 
.
ОДЗ при переходе к уравнению расширилось, наблюдаем
появление постороннего корня.
Равносильные переходы следует совершать на ОДЗ исходного уравнения.
2) Найдите ОДЗ уравнений и 
.
Проследите, как изменилось ОДЗ первого уравнения при переходе ко второму уравнению, сделайте соответствующий вывод. Сформулируйте ответ на вопрос: “На каком множестве следует выполнять равносильные переходы при решении уравнений?”
Ответ. ОДЗ первого уравнения определяется
условием
.
ОДЗ второго уравнения определяется условием 
. При переходе
от первого уравнения ко второму уравнению ОДЗ
стало уже -
. В
результате был потерян корень 
.
Равносильные переходы следует совершать на ОДЗ исходного уравнения.
3) Далее следует вернуться к первоначальной проблеме и сформулировать окончательный ответ на вопрос: “Каковы причины потери и приобретения посторонних корней при решении логарифмических уравнений?”, а также ответы на вопросы - можно ли выполнять преобразования, которые расширяют ОДЗ уравнения, можно ли выполнять преобразования, которые приводят к сужению ОДЗ уравнения?
Ответ: Посторонние корни появляются за счет расширения ОДЗ исходного уравнения. Корни теряются за счет сужения ОДЗ исходного уравнения. Допускать расширения ОДЗ можно, так как посторонние корни отсеиваются проверкой. Допускать потери корней нельзя, так как их потом не найдешь.
Теперь учащиеся понимают, что переход к
уравнению из
домашнего задания выполнять было нельзя.
Полезно познакомить учащихся с утверждением:
“Если в процессе преобразований уравнения
посторонние корни могли появиться только за счет
расширения ОДЗ, то корнями исходного уравнения
будут те и только те из них, которые входят в
ОДЗ”. Использование этого утверждения избавляет
от непосредственной подстановки полученных
корней в исходное уравнение и технической
проверки соответствующих числовых равенств. На
примере решения уравнения учителю необходимо показать
использование данного утверждения.
4) Следующая проблема может быть сформулирована так: “Источники потери и появления корней при решении логарифмических уравнений”.
В качестве возможных источников учащиеся предлагают рассмотреть потенцирование, преобразования на основе определения логарифма, логарифмических формул, основного логарифмического тождества.
III. Этап усвоения новых знаний и способов деятельности
Задача: научить учащихся составлять условия равносильности для решения логарифмических уравнений, записанных в общем виде и составлять их для конкретных уравнений.
1) Объяснение учителя.
Потенцирование
Переход от уравнения 
к уравнению
не является равносильным переходом,
так как при этом изменяется ОДЗ исходного
уравнения.
Уравнение вида можно заменить равносильной ему
системой 
(*)
системой 
(**)
Выбор системы определяется тем, какое из
неравенств решается проще: 
или 
.
Условия (*), (**) называются условиями равносильности. Неравенства определяют условие существования логарифма, равенство определяет способ решения уравнения.
Разбирается конкретный пример: 
(Ответ.
).
2) Цель дальнейшей работы состоит в том, чтобы
учащиеся научились составлять условия
равносильности для логарифмических уравнений,
записанных в общем виде и составлять их для
конкретных уравнений. Работа организуется по
группам. Каждой группе выдается одно уравнение,
для которого надо составить условия
равносильности
.
Задание. Составить условия равносильности для
решений уравнений:
3) Задание. Составить условия равносильности для решения уравнений:
Во время работы групп учитель оказывать им помощь. Представитель от каждой группы записывает на доске условия равносильности для решения уравнений в общем виде. Обсуждаются возникшие вопросы, проверяется с помощью дополнительных вопросов понимание учениками условий равносильности.
Преобразования на основе логарифмических формул
Обратить внимание учащихся на то, что при решении уравнений логарифмические формулы мы применяем в таком виде:
4) Каждая группа выясняет, как изменяется ОДЗ левой части равенства при переходе к правой части; что вследствие этого можно ожидать и как можно избежать этих последствий? Результаты работы обсуждаются всеми группами. Разбираются конкретные примеры.
Решить уравнения и 
5) Организуется работа с формулами 1° - 3° справа налево: выясняется, как изменяется ОДЗ правой части формулы при переходе к левой части (расширяется или сужается); что вследствие этого можно ожидать (появления посторонних корней или потери корней). Как можно избежать потери корней при применении формул 1° - 3° справа налево – основная задача дальнейшей работы.
Формулы требуется преобразовать так, чтобы ОДЗ, наоборот, расширить, появились бы посторонние корни, их отсеяли бы с помощью условий равносильности. Итогом должны стать формулы:
Для
справедливы формулы:
;
;
.
Разбирается решение уравнения из домашнего задания,
которое сводится к решению уравнения
.
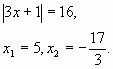
Здание выполняется на доске одним из учеников.
Как меняют ОДЗ преобразования на основе определения логарифма и формулы перехода к другому основанию, к чему они приводят – к появлению посторонних корней или к потере корней, можно дать наиболее успевающим учащимся в качестве домашнего задания.
IV. Домашнее задание
Предложить учащимся решить уравнения, для которых в ходе урока были составлены условия равносильности.
V. Рефлексия по типу “Я”, “Мы”, “Дело”
VI. Итог урока, выставление отметок
Итог урока можно провести в виде заключительного слова учителя: “При решении уравнений нужно руководствоваться следующим правилом: решение каждого уравнения необходимо проводить осознанно. Преобразования, которые приводят к потере корней, лучше не использовать. Если приходится делать преобразования, при которых могут появиться посторонние корни, то необходимо провести отбор корней. И это является необходимой частью решения, а не просто дополнительным контролем над вычислениями. Однако, использование всего теоретического “багажа” не всегда целесообразно. Если проверка полученных корней не представляет труда, то совсем необязательно выяснять, почему появились посторонние корни. Но в любом решении должна быть уверенность, что не происходит потери корней”.
Следующий урок посвящается решению логарифмических уравнений на основе знаний, приобретенных на этом уроке.
Литература для урока
- Дорофеев Г.В., Потапов М.К., Розов Н.Х., -Изд. “Наука”, Москва, 1976.
- Калягин Ю.М., Алгебра и начала анализа. Учебник для 10 класса, - Изд. “Просвещение”, Москва, 2008.
- Вавилов В.В., Мельников И.И., Олехник С.Н., Пасиченко П.И., Задачи по математике. Уравнения и неравенства. Справочное пособие, - Изд. “Наука”, Москва, 1987.