Цели урока.
Мотивация учащихся: опора на ранее изученный материал; практическая деятельность учащихся
Основные методы обучения: эвристический, репродуктивный, практический и исследовательский
Формы организации учебной деятельности: фронтальная, индивидуальная, самостоятельная, коллективная.
Техническое обеспечение урока: компьютер, мультимедийный проектор, экран, портреты математиков.
Ход урока
I. Устно. Повторение пройденного материала (используется мультимедийный проектор).
1. Какой треугольник изображен на рисунке 1?
(Прямоугольный)
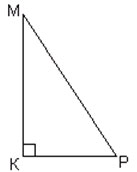
Рис. 1
2. Назовите катеты и гипотенузу.
(МК и КР – катеты, МР – гипотенуза).
3. Выразите cosM, cosP.
![]()
4. Какой треугольник на рисунке 2? Чем он интересен?
(Равнобедренный, прямоугольный. Углы при основании по 45°. Его можно достроить до квадрата со стороной, равной катету).
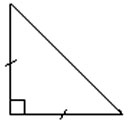
Рис. 2
5. Какой треугольник на рисунке 3?
(Прямоугольный. О – центр окружности.)
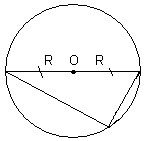
Рис. 3
II. Беседа-рассказ учителя
Сегодня вы познакомитесь с одной из немногих теорем геометрии, которую помнят все учащиеся. Но сначала я расскажу вам о математике, именем которого названа эта теорема.
В Древней Греции жил ученый Пифагор (родился он около 580 г до н.э., а умер в 500 г до н.э.). О жизни этого ученого известно немного, зато с его именем связан ряд легенд. Рассказывают, что он много путешествовал, был в Индии, Египте, Вавилоне, изучал древнюю культуру и достижения науки разных стран. Вернувшись на родину, Пифагор организовал кружок молодежи из представителей аристократии. В кружок принимались с большими церемониями после долгих испытаний. Каждый вступающий отрекался от своего имущества и давал клятву хранить в тайне учения основателя. Так, на юге Италии, которая была тогда греческой колонией, возникала так называемая пифагорейская школа. Пифагорейцы занимались математикой, философией, естественными науками. Ими было сделано много важных открытий в арифметике и геометрии. В школе существовал декрет, по которому авторство всех математических работ приписывалось Пифагору. Пифагор был убит в уличной схватке во время народного восстания. После его смерти ученики окружили имя своего учителя множеством легенд, поэтому установить правду о Пифагоре невозможно.
- Ребята, знаете ли вы что-нибудь, связанное с именем Пифагора?
(Некоторые ученики могут сформулировать саму теорему или известную фразу: “Пифагоровы штаны во все стороны равны” или рассказать о головоломке – игре “Пифагор”.)
- Обо всем этом мы и поговорим.
Запишем тему урока: “Теорема Пифагора”.
В современных учебниках теорема сформулирована так: “В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов”.
Давайте нарисуем прямоугольный треугольник (рисунок 4) и запишем эту формулировку в обозначениях:
![]()
или в виде
![]()
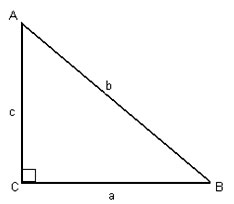
Рис. 4
Во времена Пифагора формулировка теоремы звучала так:
“Доказать, что квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на катетах”
или
“Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах”.
Теорема Пифагора имеет богатую историю. Оказывается, она задолго до Пифагора была известна египтянам, вавилонянам, китайцам и индийцам. За восемь веков до нашей эры теорема была хорошо известна индийцам под названием “правило веревки” и использовалась ими для построения алтарей, которые по священному предписанию должны иметь строгую геометрическую форму, ориентированную относительно четырех сторон горизонта.
Доказательство самого Пифагора до нас не дошло. В настоящее время имеется свыше ста различных доказательств теоремы Пифагора. Возможно, что одно из них принадлежит Пифагору или его ученику.
Вероятно, факт, изложенный в теореме Пифагора, был сначала установлен для равнобедренных прямоугольных треугольников (рисунок 5.)
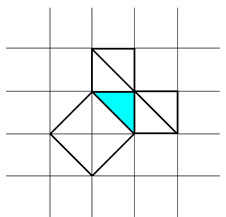
Рис. 5
Квадрат, построенный на гипотенузе, содержит четыре треугольника, а на каждом катете построен квадрат, содержащий, два треугольника. Из рисунка 6 видно, что площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.
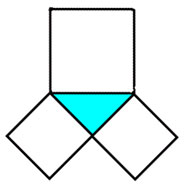
Рис. 6
- Смотрите, а вот и Пифагоровы штаны во все стороны равны”. Такие стишки придумывали учащиеся; рисовали шаржи к теореме Пифагора. Вот, например, такие, как на рисунке 7.
Рис. 7
III. Теперь докажем теорему
- Итак, докажем, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Выполним рисунок (рисунок 8) и запишем доказательство в обозначениях.
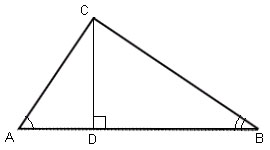
Рис. 8
(Используя наводящие вопросы, веду запись на доске, а ребята у себя в тетрадях.)
Дано: ![]()
Доказать: ![]()
Доказательство.
1. ![]()
2. Достроим ![]() до квадрата со стороной (a+b), имеем
до квадрата со стороной (a+b), имеем
![]()
3. ![]()
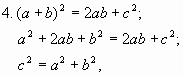
что и требовалось доказать.
IV. Закрепление данного материала (проводится с помощью мультимедийного проектора)
Задание выполняется устно:
Составьте по рисункам, используя теорему Пифагора, если это возможно, верное равенство.
1. Рисунок 9
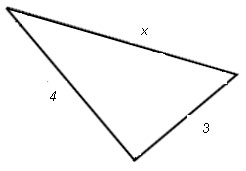
Рис. 9
(Ответ: ![]() .)
.)
Дополнительный вопрос:
- Вычислите, чему равна гипотенуза?
(Ответ: 5).
- Обратите внимание на эти три числа 3, 4, 5. треугольник с такими сторонами иногда называют египетским.
О нем вы прочитаете дома в п. 64 по учебнику Погорелова , а на следующем уроке расскажете о “Правиле веревки”.
2. Рисунок 10. О – центр окружности.
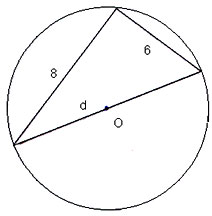
Рис. 10
(Ответ: ![]() .
Равенство можно составить, поскольку
треугольник вписан в окружность и одна из его
сторон является диаметром этой окружности.
Следовательно, треугольник прямоугольный,
поэтому можно использовать теорему Пифагора.)
.
Равенство можно составить, поскольку
треугольник вписан в окружность и одна из его
сторон является диаметром этой окружности.
Следовательно, треугольник прямоугольный,
поэтому можно использовать теорему Пифагора.)
3. Рисунок. 11.
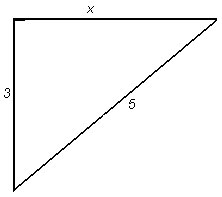
Рис. 11
(Ответ: в данном случае использовать теорему Пифагора нельзя, так как неизвестно, о каком треугольнике идет речь, а, значит, утверждать, что треугольник прямоугольный, нельзя.)
4. Рисунок 12. ![]() .
.
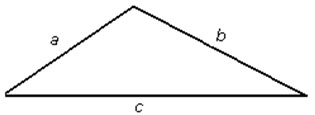
Рис. 12
(Ответ: такого треугольника не существует.)
- Итак, ребята, сделаем вывод, ответив на вопрос: на что надо обращать особое внимание при применении теоремы Пифагора?
(Ответ: чтобы использовать теорему Пифагора, надо убедиться, что треугольник прямоугольный.)
IV. Решим три старинные задачи, в которых будет работать теорема Пифагора.
Задача первая. Она взята из первого учебника математики на Руси. Называется этот учебник “Арифметика”.
- Кто из вас, ребята, знает автора первого учебника?
(Ответ: Леонтий Филиппович Магницкий.)
- Однако настоящая его фамилия Телянин, а Магницким он стал по приказу Петра I, который был восхищен его занятиями, притягивавшими к себе всех любознательных подобно магниту.
Читаю задачу так, как она была записана в те времена:
“Случится некоему человеку к стене лествицу прибрати, стены же тоя высота есть 117 стоп. И обреете лествицу долготою 125 стоп. И ведати хощет, колико стоп сея лествицы нижний конец от стены отстояти имать” (рисунок 13).

Рис. 13
На доске один из учеников выполняет чертеж (рисунок 14), объясняет и кратко записывает решение. Остальные ребята работают в тетрадях.
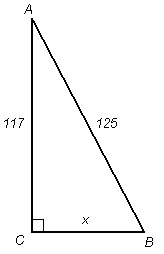
Рис. 14
Дано: ![]()
![]()
Найти: СВ.
Решение.
1. Пусть СВ= х стоп. Тогда, используя теорему Пифагора (треугольник – прямоугольный), имеем равенство:
![]()
тогда
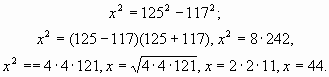
Ответ: 44 стопы.
Задача вторая. Часто математики записывали свои задачи в стихотворной форме. Вот одна из задач индийского математика ХII в. Бхаскары:
“На берегу реки рос тополь одинокий.
Вдруг ветра порыв его ствол надломал.
Бедный тополь упал. И угол прямой
С теченьем реки его ствол составлял.
Запомни теперь, что в том месте река
В четыре лишь фута была широка.
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи
У тополя как велика высота?”
(Задача иллюстрируется рисунком 15. Требуется узнать высоту тополя. Как и в предыдущей задаче, один ученик работает у доски.)

Рис.15
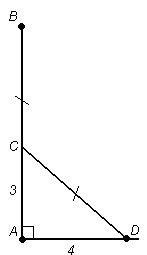
Рис. 16
Дано: ![]() (рисунок. 16).
(рисунок. 16).
![]()
Найти: АВ.
Решение.
1) ![]()
2) По теореме Пифагора
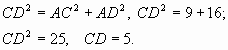
3) ![]()
Ответ: 8 футов
Задача третья. А вот еще одна задача древних индусов, тоже написанная в форме стихотворения:
“Над озером тихим,
С полфута размером, высился лотоса цвет.
Он рос одиноко. И ветер порывом
Отнес его в сторону. Нет
Боле цветка над водой.
Нашел же рыбак его ранней весной
В двух футах от места, где рос.
Итак, предложу я вопрос:
Как озера вода
Здесь глубока?”
Решение задачи:
CD – глубина озера, обозначим ее х (рисунок 17).
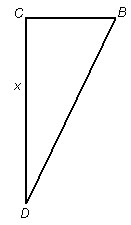
Рис. 17
Тогда по теореме Пифагора имеем:
![]() , т.е.
, т.е.
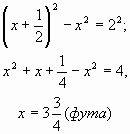
Ответ: ![]() фута.
фута.
V. Домашнее задание.
По учебнику Погорелова п. 63, 64. № 2 (3), 4, 18.
VI. Подведение итогов.
Подводится итог урока, задаются вопросы для контроля достижения целей учебной деятельности. Выставляются оценки.