Обобщающий урок в 8-м классе по теме "Квадратные уравнения. Способы решения"

Разделы: Математика

Тема урока:  «Квадратные уравнения. Способы решения »

Цели урока:

  • Обобщить и систематизировать знания учащихся по теме: «Квадратные уравнения».
  • Познакомить учащихся с устными способами решения квадратных уравнений.
  • Рассмотреть нестандартные способы решения квадратных уравнений.             
  • Расширить кругозор учащихся.
  • Повысить интерес к истории математики, к предмету.

Оборудование: карточки «Виды квадратных уравнений», «Формулы корней», таблицы Брадиса, циркули, линейки.

«Уравнение представляет собой наиболее серьёзную и важную вещь в математике».

Лодж  О.

«Посредством уравнений, теорем
Он уйму всяких разрешал проблем:
И засуху предсказывал, и ливни.
Поистине его познанья дивны»

Чосер Д.

ХОД УРОКА

I. Организационный момент

Учитель зачитывает высказывание «Уравнение представляет собой наиболее серьёзную и важную вещь в математике» и четверостишие Чосера, сообщает тему и цель урока.

II. Повторение

На доске карточки ах2 + вх + с = 0,  ах2 + 2кх + с = 0,  х2 + рх +q = 0.
Под ними хаотично расположены следующие карточки: Д = в2 – 4ас,  х1 + х2 = – р,
Д1 = к2 – ас, х1 • х2 = q,

Вопросы:

1. Какие уравнения называют квадратными?

Ученик. Квадратным уравнением называют уравнение вида ах2 + вх + с = о, где коэффициенты а, в, с – любые действительные числа, причем, а =/= 0.

2. Как называют каждое из уравнений  на карточках?

Ученик. Полное квадратное уравнение. Квадратное уравнение с чётным вторым коэффициентом. Приведённое квадратное уравнение.

3. Под каждым из уравнений расположите формулы,  по которым они решаются.

Ученик расставляет правильно карточки на доске.

4. Какие способы решения квадратных уравнений вы знаете?

Ученики.

а) вынесение общего множителя за скобки;
б) выделение квадрата двучлена;
в) по общей формуле корней квадратного уравнения;
г) по формуле для чётного второго коэффициента;
д) по теореме Виета;
е) разложение разности квадратов;
ж) графический.

Учитель. Какие учёные – математики занимались изучением уравнений, их способами решения?

Ученики. Виет. Евклид.

Учитель. Сегодня мы с вами узнаем ещё имена учёных – математиков и одно из имён у нас закодировано на доске.

5. На доске записаны уравнения, около которых прикреплены соответствующие буквы.

Задание: Найти уравнения, для которых указанный способ решения будет наиболее простым.

Вопросы:

1. Какое уравнение можно решить извлечением квадратных корней?
2. Какое уравнение решается вынесением общего множителя за скобки?
3. Какое уравнение можно решить, представляя в виде квадрата двучлена?
4. В каком уравнении надо применять общую формулу корней?
5. Какое уравнение решается по формуле, используя второй чётный коэффициент?
6. Какое уравнение удобно решить по теореме Виета?
7. Какое уравнение можно решить разложением разности квадратов?

Е      5у2 – 6у + 1= 0,
Ш     х2 = 7,
Т      6х2 + 12х = 0,
Л      х2 + 5х + 6 = 0,
И      х2 + 2х + 1 = 0,
Ф      4х2 +7х + 3 = 0,
М      х2 – 5х = х2 – 9,
Ь       х2 – 9 = 0.
После ответов на вопросы появилось ШТИФЕЛЬ.

III. Исторические сведения

Выступает ученик. (Приложение 1).

IV. Систематизация и обобщение

1. Учитель. Можно ли, не решая уравнения, определить, имеет ли оно корни или нет?
Ученик. Да, можно. Уравнение всегда имеет  корни, если  первый коэффициент и свободный член имеют противоположные знаки.
Учитель. А если они одного знака?
Ученик. Тогда надо находить дискриминант, если он больше нуля, то уравнение имеет два корня. А если равен нулю, то уравнение имеет один корень. И если дискриминант меньше нуля, то корней нет.
Учитель. Какой теоремой нужно воспользоваться, чтобы найти корни приведённого квадратного уравнения?
Ученик. Нужно воспользоваться теоремой, обратной теореме Виета.
Учитель. Сформулируйте эту теорему.
Ученик. «Если числа m и n  таковы, что их сумма равна – р, а произведение равно q, то эти числа являются корнями уравнения х2 + p x + q = 0».
Учитель. А как запишется данное условие для полного квадратного уравнения?   
Ученик. 

х1, х2 – корни полного квадратного уравнения.
В процессе ответов на следующие вопросы учащиеся заполняют таблицу 1.
1) От чего зависят знаки корней?
2) Какие знаки будут у корней?
3) Если корни одного знака, то какие положительные или отрицательные? На что смотрим?
4)  Если >0 и  <0  или > 0?
5) А если <0 и  >0, то что скажем о корнях?
6) И последнее, если  <0 и <0, то какие корни будут?

Таблица 1.

Уравнение корни уравнения
ах2 + вх + с = о >0 <0 х1 > 0,   x2 >0
 > 0 x1 < 0, x2 <0
<0 <0 | x1| > | x2|, то х1 > 0,
х2 < 0
 > 0 | x1| > | x2|, то x1 < 0,
х2 > 0

Задание. Определить имеют ли уравнения корни, и какие они по знаку.

а)3х2 – 2х – 5 = 0, т.к. 3 и –5 разных знаков, то уравнение имеет корни.
< 0, то х1 и х2 – разных знаков, а т.к.<0, то больший по модулю корень положителен.
б) х2 – 4х + 5 = 0, т.к.  и 5 одного знака, то найдём D1= k2 – ac, D1 = 3. Корни есть.
5 :  > 0, корни одного знака, а т.к. – 4 :  <0, то корни положительные. Далее ученики выполняют задание самостоятельно с последующей проверкой.
в) 4х2 + 4х – 3 = 0, ответ: корни разных знаков, больший по модулю отрицательный.
г) 5х2 – 8х + 3 = 0, ответ: D1 = 1, корни положительные.

Учитель. А сейчас мы с вами познакомимся ещё с некоторыми способами решения квадратных уравнений. Достоинство этих способов в том, что они позволяют решать уравнения устно.

2. Первый способ:  Использование свойств коэффициентов квадратного уравнения.

Учитель. На доске записаны уравнения (таблица 2). Назовите коэффициенты в каждом уравнении, и найдите их сумму, затем корни уравнения. (Ответы вносятся в таблицу).

Таблица 2

Уравнение Сумма коэффициентов Корни
х2 + х – 2 = 0 1 + 1 – 2 = 0 х1 = 1, х2 = –2
5х2 – 8х + 3 = 0 5 – 8 + 3 = 0 х1 = 1, х2 = .
7х2 – 9х + 2 = 0 7 – 9 + 2 = 0 х1 = 1, х2 =

Учитель. Посмотрите на эти уравнения, их коэффициенты и корни. Попробуйте найти какую – то закономерность в корнях этих уравнений, в соответствии между отдельными коэффициентами и корнями, в сумме коэффициентов.
Ответы учеников: один из корней равен 1, второй корень равен свободному члену или  частному от деления свободного члена на первый коэффициент, сумма коэффициентов равна нулю.
Учитель. Какой вывод можно сделать?
Ученик. Если в квадратном уравнении ах2 + вх + с = 0 сумма коэффициентов равна нулю
(а + в + с = 0), то один из корней равен 1, а другой .
Учитель. Есть ещё одно свойство коэффициентов. Пусть дано квадратное уравнение
ах2 + вх +с = 0, где а =/=0. Если а – в + с = 0 или в = а + с, то х1 = –1, х2 = – .
Запись на доске и в тетрадях.

Таблица 3.

Уравнение Свойство коэффициентов Корни уравнения
ах2 + вх + с = 0

а + в + с = 0

 х1 = 1, х2 =
а – в + с = 0 или в = а + с х1 = –1, х2 = –

Учитель. На доске записаны уравнения. Решить уравнения, используя свойства коэффициентов.
Ученик выполняет решение уравнений на доске, остальные записывают в тетрадях. 
г) 11х2 + 27х + 16 = 0,  11 + 16 = 27  (в = а + с), х1 = – 1, х2 = – .
д) 313х2 – 326х + 13 = 0, 313 – 326 +13 = 0 (а + в + с = 0), х1 = 1, х2 = .

3. Учитель. Второй способ применяют, когда дискриминант есть точный квадрат и легко можно найти корни уравнения, используя теорему Виета. Это метод «переброски».
Рассмотрим квадратное уравнение ах2 + вх + с = 0 (1). Умножим обе его части на а, получим 
а2х2 + авх + са = 0. Пусть ах = у, тогда у2 + ву +ас = 0. Его корни у1 и у2, найдём корни уравнения (1) с помощью теоремы Виета. Отсюда  получаем х1 =   и х2 = .
При этом способе коэффициент «а» умножается на свободный член, как бы перебрасывается к нему, поэтому его и назвали  «методом переброски»».[8] Решим уравнения. Учитель решает на доске, привлекая к решению учащихся.
а) 2х2 – 11х + 15 = 0, D = 121 – 4 • 2 • 15 = 121 – 120 = 1. 
б) 2х2 – 9х + 9 = 0,   D = 9.
Умножим на 2 обе части уравнения, получим у2 – 9у + 18 = 0
22х2 – 2 • 11х + 30 = 0, обозначим 2х через у.
Получим  у2 – 11у + 30 = 0, по теореме Виета 
=>    =>                                   =>    => 
Ответ: 3; 2,5.                                                                Ответ: 3; 1,5.
Ученик решает у доски.
в) 4х2 + 12х + 5 = 0,   D = 64.                                  г) 10х2 – 11х + 3 = 0,      D = 1.
у2 + 12у + 20 = 0,                                                      у2 – 11у + 30 = 0,    
 =>   =>                     =>   => 
Ответ: –0,5; –2,5.                                                          Ответ: 0,6; 0,5.

4. Решение квадратных уравнений с помощью циркуля и линейки

Рассказывает этот способ ученик. Чертежи проецируются на экран.

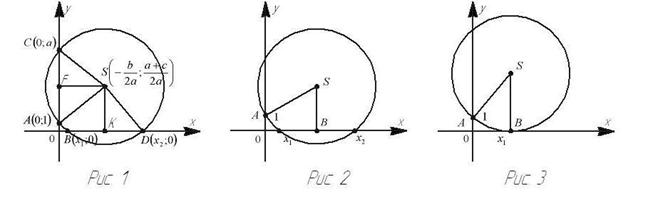
Нам известен графический способ решения квадратных уравнений с помощью параболы. Рассмотрим ещё способ нахождения корней квадратного уравнения ах2+ вх + с = о  с помощью циркуля и линейки (рис. 1).

«Допустим, что искомая окружность пересекает ось абсцисс в точках В (х1;0) и D (х2;0), где х1 и х2 – корни уравнения ах2 + вх + с = 0, и проходит через точки А(0;1) и С (0; ) на оси ординат. Тогда по теореме о секущих имеем ОВ . ОD = ОА . ОС, откуда ОС =  = = .
Центр окружности находится в точке пересечения перпендикуляров SF и SK,
Восстановленных в серединах хорд АС и ВD, поэтому

SF =   =  =

SK =  = = – ,

Итак:

  1. построим точки S(–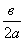; 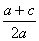) (центр окружности) и А (0;1);
  2. проведём окружность с радиусом SA;
  3. абсциссы точек пересечения этой окружности с осью Ох являются корнями исходного квадратного уравнения.

При этом возможны три случая.

1) Радиус окружности больше ординаты центра (АS > SВ или R>), окружность пересекает ось Ох в двух точках (рис.1) В (х1; 0) и D (х2; 0), где х1 и  х2 – корни квадратного уравнения ах2+ вх + с = 0.

AS > SB, R > . (рис.2)  Два решения х1 и х2.

2) Радиус окружности равен ординате центра (AS = SB, или R = ), окружность касается оси Ох (рис.3) в точке В (х1;0), где х1 – корень квадратного уравнения.
AS = SB, R =. Одно решение х1.

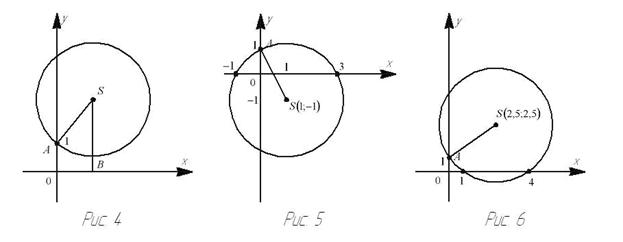
3) Радиус окружности меньше ординаты центра (AS < SB,  R<),окружность не имеет общих точек с осью абсцисс (рис.4), в этом случае уравнение не имеет решения.
AS < SB, R < .    Нет решения.

Примеры.

1. Решим уравнение     х2 – 2х – 3 = 0    (рис.5)

Решение. Определим координаты точки центра окружности по формулам:
х = –   у =
Проведём окружность с центром в точке S(1;–1) и радиуса SA, где А(0;1).

Ответ: х1 = –1, х2 = 3.

2. Решим уравнение    х2 –5х + 4 = 0  (рис.6)

Решение. Определим координаты  точки центра окружности  по формулам:
х = –  у =

Проведём окружность с центром в точке S(2,5; 2,5) и радиуса SA, где А (0;1).

Ответ: х1 = 1, х2 = 4.

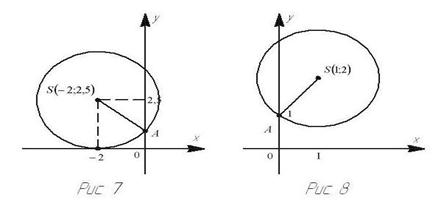
3. Решим уравнение    х2 + 4х + 4 = 0  (рис.7)

Решение. Определим координаты точки центра окружности по формулам:
х = –,  у =
Проведём окружность с центром в точке S(–2; 2,5) и радиуса SA, где А (0;1).
Ответ: х = – 2.

4. Решим уравнение х2 – 2х + 3 = 0  (рис.8)

Решение. Определим координаты точки центра окружности по формулам:
х = –,   у =

Проведём окружность с центром в точке S(1;2) и радиуса SA, где А (0;1).

Ответ: уравнение не имеет решения.

Решить с помощью циркуля и линейки следующие уравнения:

Вариант 1            1) х2 – 3х + 2 = 0;                          4) 2х2 – 7х + 5 = 0;
Вариант 2            2) х2 – 3х – 10 = 0;                        5) х2 – 6х + 9 = 0; [8]

5. Решение квадратных уравнений с помощью номограммы

Этот способ решения квадратных уравнений, помещён на стр.83 Четырёхзначных математических таблиц  В.М. Брадиса.
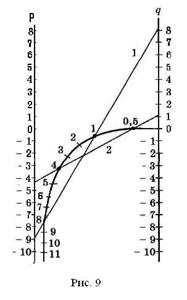
Рисунок 9. Номограмма для решения уравнения z2 + pz + q = 0.
Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициентам определить корни уравнения. Если дано полное квадратное уравнение, то его надо привести к приведённому квадратному уравнению z2 + pz + q = 0 (1). Затем второй коэффициент (р) и свободный член  (q) из уравнения (1)  отметить на  соответствующих осях р и q, полученные точки соединить прямой.
Прямая пересекает кривую шкалу в  двух точках – корнях данного уравнения, если корни положительные. Если уравнение имеет корни разного знака, то прямая пересечёт кривую шкалу в одной точке – это положительный корень. Отрицательный корень находят, вычитая положительный корень из – р. Если же корни отрицательные, то  по номограмме находят два положительных корня  t1 и  t2 для уравнения z2 – pz + q = 0, а для уравнения z2 + pz +q = 0 корнями будут z1 = –t1, z2 = –t2.
Решим уравнения с помощью номограммы. На доску проецируется номограмма и с помощью её решаются уравнения, а учащиеся по таблице Брадиса.

a) z2 – 7z + 6 = 0.
Ответ: 6; 1.     

б) z2 – 4z + 4 = 0.
Ответ: 2.     

в) z2 + 5z + 4 = 0.
Ответ: –4; –1.

Пример. z2 – 9z + 8 = 0, p = –9, q = 8, тогда z1 = 8 и z2 = 1.
Решим с помощью номограммы уравнение 2z2 – 9z + 2 = 0.
Разделим коэффициенты этого уравнения на 2, получим уравнение z2 – 4,5z + 1 = 0. На оси p отметим число –4,5 ,а на оси q число 1.Соединяем точки прямой и номограмма даёт корни z1= 4 и z2 = 0,5 (рис.9)

V. Домашнее задание

№ 641(а, б, в), № 586.

VI. Самостоятельная работа

1 вариант                                                      2 вариант

1) Не решая уравнения определить знаки корней.

2х2 – 5х + 2 = 0                                             3х2 + 14х + 16 = 0

2) Решить уравнение, используя

а) свойство коэффициентов

х2 + 23х + 24 = 0                                           х2 + 15х – 16 =0

б) метод переброски

3х2 + 11х +6 = 0                                            2х2 + х – 10 = 0

в) с помощью циркуля и линейки

х2 + 4х +3 = 0                                                х2 + 4х + 5 = 0

г) с помощью номограммы

z2 – z – 6 = 0                                                  z2 – 9z + 8 = 0

Литература. 

  1. Макарычев Ю. Н. и др. Алгебра 8.
  2. Окунев A.K. Квадратные функции, уравнения и неравенства. М., «Просвещение»,1972.
  3. Пресман А.А. Решение квадратного уравнения с помощью циркуля и линейки. – М., Квант, № 4/72, с.34.
  4.  Пичурин Л.Ф. За страницами учебника алгебры.– М., «Просвещение», 1990.
  5. Г.И. Глейзер. История математики в школе, 7–8 кл. – М., «Просвещение», 1982.
  6. Брадис В.М. Четырёхзначные математические таблицы для средней школы.– М., «Просвещение», 1990.
  7. М., Математика (приложение к газете Первое сентября), №№ 21/96, 10/97, 24/97, 18/98, 21/98, 42/2000, 42/2001,48/2001, 35/2004.
  8. М., Математика (приложение к газете Первое сентября), № 40/ 2000.
  9. Злоцкий Г.В. Карточки-задания при обучении математике. Книга для учителя. – М., «Просвещение»,1992.