Задание 1. Вычислить 
, если 
.
Решение. Т. к 
то существуют такие 
и 
, что 
Тогда 
.Тогда выражение
Ответ :0.
Задание 2.Среди чисел(x;y;z;v)системы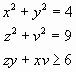 
найти такие, при каждом из
которых 
принимает
наибольшее значение.
Решение. Внимательно изучив первое и второе
уравнения системы, обозначим 
.
Неравенство системы примет вид: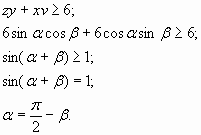 
Тогда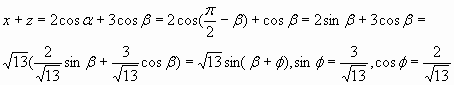 
.
Таким образом, наибольшее значение искомого
выражения равно 
.
Найдем искомые числа.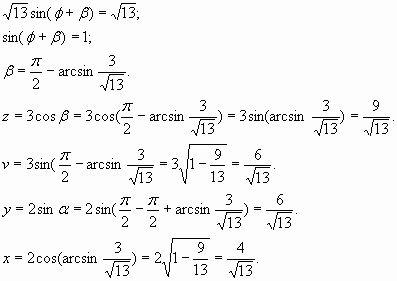 
Ответ: 
Задание 3. Решить уравнение 
Решение. О.Д.З. 
.Пусть 
, тогда уравнение примет вид:
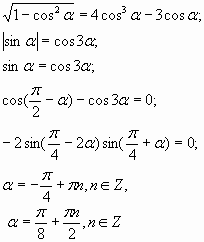
Из полученных серий выберем только те корни,
которые удовлетворяют условию 
. Это числа 
Таким образом, исходное уравнение равносильно совокупности
.
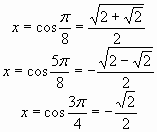Эти числа и являются корнями данного уравнения.
Задание 4. Решить систему уравнений 
.
Решение. Введем замену 
.
Второе уравнение системы примет вид:
.
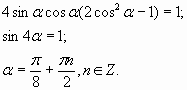Из найденной серии в промежуток 
попадают числа 
Для 
: 
.
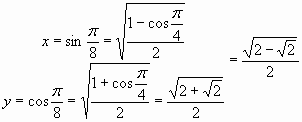Аналогично находятся и остальные три пары решений.
Ответ: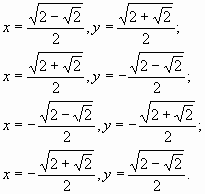 
Задание 5.
Последовательность чисел
задана условиями 
и для всех 
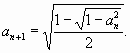Доказать,
что сумма любого количества чисел 
меньше 1,03.
Решение. Можно увидеть, что 
. Тогда
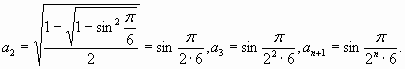
Рассмотрим сумму 
. Воспользуемся известным неравенством
, тогда
.
Задание 6. Доказать, что при любых
действительных x и y верно неравенство: 
Решение. Введем замену : 
, где 
.
Тогда 
.
Отсюда следует справедливость доказываемого неравенства.