I Основные понятия функции нескольких переменных
1.1 Понятие функции нескольких переменных
Пусть D – некоторое множество пар действительных чисел и пусть каждой паре (x; y) из D поставлено в соответствие число Z. Тогда говорят, что на множестве D задана функция двух переменных Z = f(x,y).
Переменные x,y называют независимыми переменными (или аргументами), Z - зависимой переменной; говорят также, что f(x,y) есть значение функции f в точке (x;y).
Множество D называют областью определения функции.
Все значения, которые принимает функция f(x,y) (при (x,y) принадлежащих области её определения), образуют область значений функции.
Аналогично можно ввести понятие функции трех переменных u = f(x,y,z), определенной на множестве D, состоящем не из действительных чисел (как для функции одной переменной) и не из пар действительных чисел (как для функции двух переменных), а из троек действительных чисел (x,y,z), рассматриваемых в определенном порядке. Можно ввести понятие функции четырех, пяти и вообще любого конечного числа переменных – все такие функции называют функциями нескольких переменных.
Примеры функций нескольких переменных:
S = xy – площадь прямоугольника со сторонами x, y есть функция двух переменных;
U = IR (закон Ома) – напряжение U на участке электрической цепи есть функция двух переменных: силы тока I и сопротивления R;
V = xyz - объем прямоугольного параллелепипеда со сторонами x,y,z есть функция трех переменных.
Чтобы задать функцию двух (трех) переменных, нужно указать способ, с помощью которого для каждой пары (тройки) значений аргументов можно найти соответствующее значение функции.
Наиболее употребительным (как и в случае функций одной переменной) является способ задания функции с помощью формулы Z = f(x,y), где f(x,y) – некоторое выражение с переменными x,y. В таком случае говорят, что функция задана формулой или что функция задана аналитически.
Значение функции Z = f(x,y) в точке M(x0,y0) называется частным значением функции и обозначается f(x0,y0) или f(M).
Пример:
Дана функция 
Вычислить 
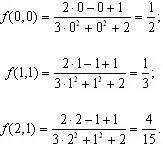
1.2 Область определения
Область определения функции Z = f(x,y)в простейших случаях представляет собой либо часть плоскости, ограниченную замкнутой кривой, причем точки этой кривой (границы области) могут принадлежать или не принадлежать области определения, либо всю плоскость, либо, наконец, совокупность нескольких частей плоскости xOy
Геометрическим изображением функции Z = f(x,y) в прямоугольной системе координат Oxyz (графиком функции) является некоторая плоскость.
Для аналитически заданной функции иногда не указывают явно область ее определения. В таком случае подразумевают, что область определения функции Z = f(x,y) совпадает с областью определения выражения Z = f(x,y), т.е. с множеством тех значений x,y, при которых выражение f(x,y) имеет смысл.
Пример: Найти область определения функции:
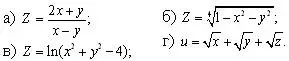
а) Функция не определена лишь в случае, когда y = x. Геометрически это означает, что область определения функции состоит из двух полуплоскостей, одна из которых лежит выше, а другая ниже прямой y = x.
б) Функция определена при условии 
,
т.е. . Это круг с центром в начале координат и
радиусом 
, включающий свою границу, т.е. окружность 
=
1.
в) Функция определена при условии -
4 > 0, т.е. > 4. Это часть плоскости, лежащая
вне круга с центром в начале координат и радиусом
2, не включающая границу круга, т.е. окружность =
4
г) Функция определена при (x,y,z),
удовлетворяющих одновременно условиям x 
0, y 0, z 0.
1.3 Частные производные
Пусть задана функция Z = f(x,y).
Переменной x дадим приращение dx, а y оставим без изменения. Если существует предел:
то он называется частной производной от функции Z = f(x,y) по переменной x.
Обозначать частную производную от функции Z = f(x,y) по переменной x можно любым из символов:
Чтобы найти частную производную от функции Z = f(x,y) по переменной x, нужно найти производную от этой функции по x, считая, что x является постоянной.
Аналогично, частной производной от функции Z = f(x,y) по переменной y, называется предел:
и обозначается одним из символов:
Частная производная от функции Z = f(x,y) по
переменной y - это производная от
функции Z = f(x,y) по переменной 
в предположении, что x = const..
Частные производные от функции нескольких переменных находятся как производные от функции одной переменной при условии, что все остальные переменные считаются на момент дифференцирования постоянными.
Частными производными второго порядка от функции Z = f(x,y) называются частные производные от частных производных первого порядка:
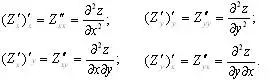
Частные производные
называются
смешанными частными производными второго
порядка.
В точках, где смешанные производные непрерывны, они равны, т.е.:
Для частных производных справедливы обычные правила и формулы дифференцирования.
Пример 1. 
Найти 
.
Рассматривая y как постоянную величину, получим
Рассматривая x как постоянную, найдем
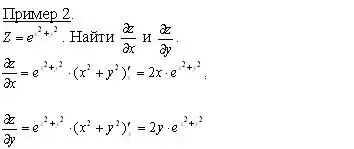
Пример 3. 
Найти 
Найдем частные производные:
Дифференцируя повторно, получим
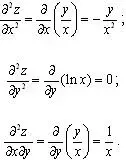
Пример 4. 
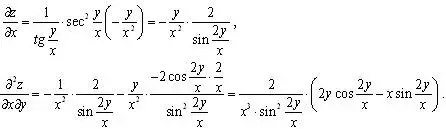
Пример 5.
.
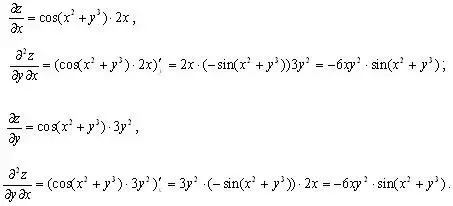
Пример 6. Требуется показать, что функция 
удовлетворяет равенству:
Найдем частные производные первого порядка
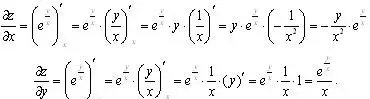
Найдем смешанную производную
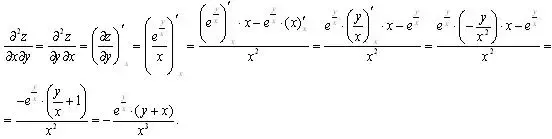
Подставим найденные производные в равенство
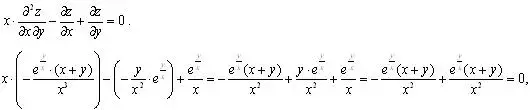
т.е. равенство верно.
Ответ: Функция удовлетворяет равенству .