Надо ли учить школьников решать прикладные задачи с физическим, математическим, экономическим содержанием? С одной стороны законы математики обязательны для всех наук. Круг ее приложений настолько широк, что все равно не удается рассмотреть их в достаточной полноте. И, наконец, учить решать физические задачи дело преподавателя физики. С другой стороны математика черпает идеи для своего дальнейшего развития именно из приложений. Если вообще отказаться от задач с реальным предметным содержанием, то ученые не смогут решать ничего, кроме теоретических упражнений.
Последние годы отмечена тенденция все более широкого проникновения математики в различные области наук, казалось бы, далеких от математики (биология, химия, экономика, социология, медицина). Расширились прикладные возможности и в индустриальной, информационной сферах. Необходимо отразить эти возможности в образовательном процессе, и так как я работаю в классах инженерно-технического профиля, то мне необходимо подготовить учащихся к использованию математических знаний в качестве инструмента познания, когда они сталкиваются с проблемой решения задач соответствующего содержания.
Цель данной разработки заключается в том, чтобы помочь организовать профильное обучение в инженерно-техническом классе.
Задачи:
- показать, как практика влияет на развитие математики, и как математика помогает практике в решении ее проблем;
- создать задачи, не придуманные в математических целях, а возникающие на самом деле в различных областях практической деятельности человека;
- расширить знания учащихся по математике с помощью формирования навыков системного, математического подхода к изучению естественно научных проблем.
Опыт показывает, что использование прикладных задач в преподавании математики только тогда может дать педагогический эффект и вызвать интерес у учащихся, если эти задачи удовлетворяют следующим требованиям:
- допускают краткую формулировку;
- использующиеся в них понятия известны учащимся, легко определяемы или интуитивно ясны;
- применение математического аппарата не требует существенной затраты времени;
- решение задач имеет важное практическое значение.
Не следует рассматривать с учащимися такие задачи, в которых описание "прикладной части" отнимает много времени, тогда как применение математического аппарата занимает всего несколько строк. Очевидно, что педагогическая ценность прикладной задачи увеличивается, если ее решение непосредственно связано с излагаемым материалом.
Приведу несколько прикладных задач, удовлетворяющих перечисленным требованиям. Перед формулировками задач дам краткие описания тех ситуаций, при которых они возникают. Такие описания может делать и учитель, чтобы пояснить употребляемые термины, сделать более наглядными затрагиваемые технические проблемы и тем самым усилить интерес учащихся к предложенным задачам.
I
Одно из простейших применений метода координат в инженерной практике связано с решением
геодезических задач. Рассмотрим две такие задачи, которые возникают при проектировании лесных просек или горных тоннелей, т.е. в тех случаях, когда полностью исключается возможность непосредственных измерений.
Прямая геодезическая задача
Найти положение конечной точки B некоторой трассы, зная ее начальную точку А, протяженность l = АВ и направление, которое определяется азимутом а – углом наклона трассы к вертикальной оси.
Решение
По плану местности, к которой относится проектируемая трасса, определяются прямоугольные координаты (x1; y1) начальной точки А, а координаты (х2; у2) точки В вычисляются по формулам (рис. 1).
х2 = x1 + lcosa; у2 = y1 + lsina
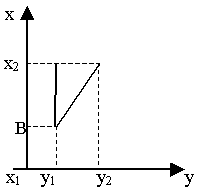
Рис. 1
Заметим, что в геодезии вертикальную ось обозначают через ох, а горизонтальную – через оу.
Обратная геодезическая задача
По координатам начальной точки и конечной точки трассы АВ (рис. 1) найти ее протяженность и направление. Для решения следует воспользоваться следующими известными формулами:
l = AB = ![]()
Нельзя не обратить внимания на простоту и впечатляющий эффект геодезических задач. Они убедительно показывают учащимся, какое важное практическое применение может иметь метод координат, и в частности формула расстояния между двумя точками.
II
Приведу простой пример практического использования понятия касательной к графику функции. Рассмотрим задачу, связанную с проектированием мостов большой длины. Нормальная эксплуатация моста возможна только в том случае, если профиль моста (он изображен на рис. 2) не имеет изломов. Для этого нужно, чтобы переход от прямых AM и BN к параболе АОВ был плавным, т.е. чтобы прямые AM и BN были касательными к параболе в точках сопряжения А и В.
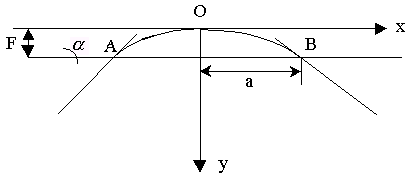
Рис. 2
Задача
Тангенс угла наклона прямых AM и BN к горизонту равен m, стрела провеса моста f. Каким должно быть уравнение параболы АОВ, чтобы профиль моста не имел изломов?
Решение
Выберем систему координат так, как показано на
рис. 2. Обозначим через а неизвестную абсциссу
точки В. Тогда уравнение параболы у = kx2
имеет вид: у = ka2, отсюда у'= 2ka.
Исходя из условия, запишем: f = ka2 и m = 2ka,
тогда а = ![]() и k =
и k = ![]() . Следовательно, уравнение
параболы имеет вид: у =
. Следовательно, уравнение
параболы имеет вид: у = ![]() .
.
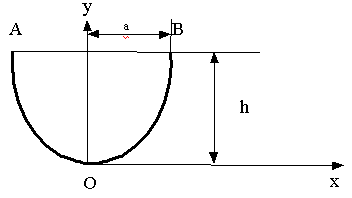
Рис. 3
III
Приведу простой прикладной пример на вычисление площади фигуры с помощью интеграла.
Каналы, используемые для водоотвода и орошения, нередко имеют форму параболических лотков. Для того, чтобы определить гидравлически наивыгоднейшее живое сечение такого канала, необходимо знать площадь лотка.
Задача
Найти формулу площади параболического сегмента, который имеет основание 2а и высоту h (рис. 3).
Решение
Запишем уравнение параболы АОВ(АВ=2а) в виде у = kx2.
Так как точка В (a;h) принадлежит параболе, то h = ka2,
откуда k=![]() . Если S – площадь данного сегмента, то
. Если S – площадь данного сегмента, то ![]() S = ah –
S = ah – 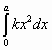 = ah –
= ah – ![]() ka3 =
ka3 = ![]() ah, откуда
S =
ah, откуда
S = ![]() ah =
ah = ![]() ABh
ABh
Ответ: S = ![]() ABh.
ABh.
Применение производной в практической деятельности
Геодезия. При изучении геометрии мы встречаемся со способом определения высоты предмета с помощью угломерных инструментов. При топографических съемках местности аналогичный прием используется для определения превышения одной точки земной поверхности над другой. Этот способ дает хороший результат, если рассматриваемые точки находятся на незначительном расстоянии. В противном случае начинает сказываться кривизна Земли и возникает существенная погрешность.
Если расстояние между точками В и С достаточно велико, то к найденному (с помощью угломерных инструментов) значению превышения точки В над точкой С прибавляют так называемую поправку на кривизну Земли:
![]() , где
R – радиус Земли, l — длина
горизонтальной проекции BC.
, где
R – радиус Земли, l — длина
горизонтальной проекции BC.
Задача 1
Объясните происхождение указанной выше формулы для поправки
h.
Решение
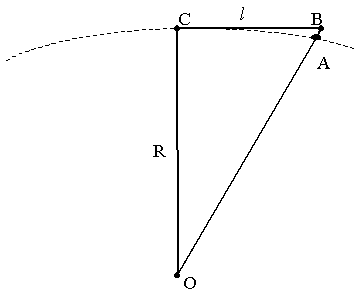
Рис. 4
Рассмотрим рис. 4, на котором штрихами
изображена поверхность океана, точка О – центр
Земли. Пусть, для простоты, точка С лежит на
поверхности океана, а точка В принадлежит
горизонтальной плоскости, проходящей через
точку С. Так как в таком случае угол между лучом
СВ и горизонтальным направлением (оно
определяется с помощью отвеса) равен нулю, то из
точки С нам покажется, что точки В и С имеют
одинаковую высоту. Согласившись с этим, мы
допустим погрешность: ![]() h = АВ = ОВ – О А =
h = АВ = ОВ – О А = ![]() – R.
– R.
Величина
l относительно мала по сравнению с R. Поэтому для вычисления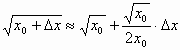 ,
полученной в курсе "Алгебра и начала анализа
10–11" автор А.Н. Колмогоров. Положив в этой
формуле x0 = R2,
,
полученной в курсе "Алгебра и начала анализа
10–11" автор А.Н. Колмогоров. Положив в этой
формуле x0 = R2, ![]() h =
h = ![]() - R
- R ![]() +
+ ![]()
где R – радиус Земли, l – длина горизонтальной проекции отрезка ВС.
Транспорт. В практике проектирования сети автомобильных дорог часто возникает необходимость устройства узла разветвления. Местоположение узла и взаимное расположение проходящих через него дорог определяется комплексом экономических и географических условий, но первый, предварительный этап решения этой задачи учитывает лишь затраты рабочего времени на перевозки, причем в качестве вспомогательной решается вначале следующая задача.
Задача 2
Каким должен быть угол примыкания
(рис. 5) дороги СЕ к автомагистрали АВ, чтобы затраты времени на перевозки по маршруту AEC были наименьшими, если скорость движения автомобилей по магистрали планируется равной Vm, а по подъездной дороге – Va(Vm > Va).
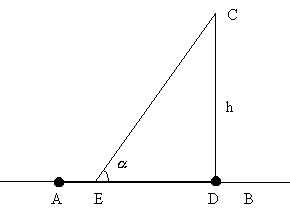
Рис. 5
Проведем из точки С перпендикуляр к прямой АВ и обозначим длину отрезка CD через h, а длину отрезка AD через l. Тогда получим:
СЕ = ![]() , DE = h • ctg
, DE = h • ctg![]()
Отсюда находим время движения автомобиля по маршруту AEC:
![]()
Так как точка А в наших рассуждениях
зафиксирована условно, определяя лишь
направление движения по магистрали, то ![]() может
изменяться в промежутке (0;
может
изменяться в промежутке (0;![]() ).
).
Задача свелась к отысканию наименьшего
значения функции t(![]() ) на указанном промежутке.
) на указанном промежутке.
Найдем производную: t'(
Так как 0 < ![]() < 1, то производная на рассматриваемом
промежутке обращается в нуль лишь в одной точке
< 1, то производная на рассматриваемом
промежутке обращается в нуль лишь в одной точке
![]() 0 = arccos
0 = arccos ![]() , (1).
, (1).
Причем t'(![]() ) < 0 при
) < 0 при
Это означает, что на промежутке (0;![]() 0]
функция t убывает, а на промежутке [
0]
функция t убывает, а на промежутке [![]() ;
;![]() ) –
возрастает. Следовательно, рассматриваемая
функция t при
) –
возрастает. Следовательно, рассматриваемая
функция t при ![]() =
= ![]() достигает наименьшего значения.
достигает наименьшего значения.
Ответ: угол примыкания
определяется по формуле ![]() = arccos
= arccos ![]()
Мелиорация. Площадь ![]() поперечного сечения канала
(целиком заполнен водой) называют его живым
сечением, а длину X границы такого сечения
называют смоченным периметром канала. С помощью
теоретических расчетов и эксперимента
установлено, что из всех каналов с заданным живым
сечением наибольшей пропускной способностью и
одновременно наименьшей фильтрацией отличаются
каналы с наименьшим смоченным периметром. Про
такие каналы говорят, что они имеют
гидравлически наивыгоднейший профиль.
поперечного сечения канала
(целиком заполнен водой) называют его живым
сечением, а длину X границы такого сечения
называют смоченным периметром канала. С помощью
теоретических расчетов и эксперимента
установлено, что из всех каналов с заданным живым
сечением наибольшей пропускной способностью и
одновременно наименьшей фильтрацией отличаются
каналы с наименьшим смоченным периметром. Про
такие каналы говорят, что они имеют
гидравлически наивыгоднейший профиль.
В мелиоративной практике часто сооружаются каналы или лотки с поперечным сечением в форме прямоугольника, треугольника, трапеции и сегмента круга. Поэтому представляет интерес расчет гидравлически наивыгоднейшего профиля для каналов такой формы.
Задача 3
При каком отношении глубины к ширине канал прямоугольного сечения имеет гидравлически наивыгоднейший профиль?
Решение
Рис. 6
Пусть х – ширина канала, ![]() - его живое сечение. Тогда
глубина канала
- его живое сечение. Тогда
глубина канала ![]() , а его смоченный периметр ( рис. 6 ) : X(x) = x +
, а его смоченный периметр ( рис. 6 ) : X(x) = x + ![]() , X'(x) =
, X'(x) = ![]() .
.
Так как Х'(![]() ) = 0, Х'(х) < 0 при 0 < х <
) = 0, Х'(х) < 0 при 0 < х < ![]() и X'(х)
и X'(х) ![]() 0 при х >
0 при х > ![]() , то функция X в
точке
, то функция X в
точке ![]() достигает наименьшего значения.
достигает наименьшего значения.
Итак, ширина канала в рассматриваемом случае
должна быть ![]() ,
глубина
,
глубина ![]() .
.
Ответ : ![]() .
.
Задача 4
РешениеСечение канала – сегмент круга (рис. 7). Каким должен быть центральный угол
(0<
<=
), чтобы канал имел гидравлически наивыгоднейший профиль?
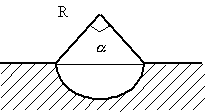
Рис. 7
Пусть R – радиус круга. Живое сечение канала
найдем как разность площадей сектора и
треугольника:![]()
![]() .
.
Отсюда получаем, что R= ![]() , и значит, смоченный
периметр X(
, и значит, смоченный
периметр X(![]() )=R
)=R![]() =
=![]()
![]()
Исследуем более простую функцию f(![]() ) =
) = ![]() . При 0<
. При 0<![]() <
<![]() имеем:
имеем:
f '(![]() ) =
) = ![]()
![]()
 .
.
Так как sin![]()
![]()
![]() и
и ![]() на рассматриваемом
интервале, то производная на (0;
на рассматриваемом
интервале, то производная на (0;![]() )
определена и отрицательна. Поэтому функция f, а
значит, и X убывает на (0;
)
определена и отрицательна. Поэтому функция f, а
значит, и X убывает на (0;![]() ). В силу непрерывности
функции X на промежутке (0;
). В силу непрерывности
функции X на промежутке (0;![]() заключаем, что X убывает и на
таком промежутке. Следовательно, функция X
достигает наименьшего значения при
заключаем, что X убывает и на
таком промежутке. Следовательно, функция X
достигает наименьшего значения при![]() . В
сечении канала должен быть полукруг.
. В
сечении канала должен быть полукруг.
Ответ : ![]() .
.
Строительство. При монтаже промышленных и сельскохозяйственных зданий небольшой высоты широко используются автомобильные краны. Для правильного выбора крана необходимо знать многие исходные данные о сооружаемом объекте. В частности, габаритные данные объекта позволяют заранее определить требуемую длину стрелы крана. Рассмотрим эту задачу
Задача 5
Вывести формулу для определения длины стрелы автомобильного крана, с помощью которого можно построить здание высоты Н и ширины 2
c плоской крышей.
Решение
Так как автомобильный кран может перемещаться вокруг всего здания, то крюк его крана достанет до любой точки здания, если он достанет (рис. 8) до середины крыши (имеется в виду середина по ширине).
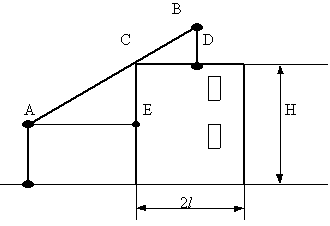
Рис. 8
Рассмотрим кран, который находится
в точке О, подает деталь на середину крыши. Пусть
угол наклона стрелы при этом составляет ![]() . Тогда BC=
. Тогда BC= ![]() =
=![]() ; AC =
; AC = ![]() =
=![]() , где h = АО
– высота подвеса стрелы крана. В таком случае
длина стрелы крана
, где h = АО
– высота подвеса стрелы крана. В таком случае
длина стрелы крана ![]()
![]() +
+![]() (1)
(1)
Из формулы (1) видно, что для совершения
указанной работы краном, установленным в другой
точке (ближе к зданию или дальше от него),
потребуется кран с другой длиной стрелы,
поскольку при таком перемещении меняется угол ![]() .
Определим наивыгоднейшее место установки крана,
т.е. такое место, с которого заданная работа может
быть выполнена краном с наименьшей длиной
стрелы. Для этого, очевидно, достаточно
определить, при каком,
.
Определим наивыгоднейшее место установки крана,
т.е. такое место, с которого заданная работа может
быть выполнена краном с наименьшей длиной
стрелы. Для этого, очевидно, достаточно
определить, при каком, ![]() из промежутка (0;
из промежутка (0;![]() ) функция l
принимает наименьшее значение.
) функция l
принимает наименьшее значение.
Найдем производную функции ![]()
Производная обращается в нуль лишь в одной
точке ![]() 0=
arctg
0=
arctg![]() и функция l достигает своего
наименьшего значения при
и функция l достигает своего
наименьшего значения при ![]() 0=
arctg
0=
arctg![]() .
.
Найдя из полученной формулы значение
Деревообработка. Важное народнохозяйственное значение имеет рациональный раскрой древесины. Комплексное решение таких задач требует применения довольно глубоких методов классической и современной математики. Однако отдельные задачи такого рода можно решить, используя только производную.
Задача 6
На лесопильных рамах (они предназначены для продольного пиления) бревна часто распиливают на квадратный брус и четыре доски (рис. 9) с максимально возможной площадью поперечного сечения. Какой должна быть расстановка пил для такой распиловки?
Решение
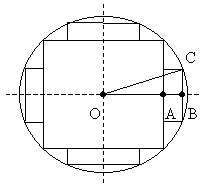
Рис. 9
Из рис. 9 видно, что для ответа на вопрос задачи
достаточно определить толщину выпиливаемых
досок. Так как сторона квадрата, вписанного в
окружность радиуса r, равна r![]() , то ОА =
, то ОА = ![]() .
.
Пусть толщина доски АВ = х, тогда ее ширина 2ВС =![]() =
=![]() , а
площадь поперечного сечения:
, а
площадь поперечного сечения:
S(x) = 2![]()
![]() =
= ![]() .
.
Требуется узнать, при каком х из отрезка [0;![]() ] функция
S достигает наибольшего значения.
] функция
S достигает наибольшего значения.
Найдем производную : S'(x) =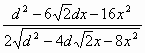 .
.
Критическая точка: x0=![]() Так как
S(0) = S
Так как
S(0) = S![]() ,
а S(x0)' > 0, то доски толщиной 0,10d имеют
наибольшую площадь поперечного сечения.
,
а S(x0)' > 0, то доски толщиной 0,10d имеют
наибольшую площадь поперечного сечения.
Ответ: 0,10d.
Сельское хозяйство и животноводство. Усилению политехнической и трудовой направленности обучения математике способствует решение задач практического характера. Многие из этих задач сводятся, как известно, к нахождению наибольшего или наименьшего значения функции на некотором промежутке.
Задача 7
Пастбищные водопоильные желоба для коров иногда устраивают из трех одинаковых досок, сбивая их под некоторым тупым углом величины
. Каким должен быть угол
, чтобы получился желоб наибольшей вместимости? (рис. 10)
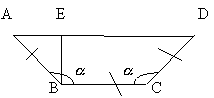
Рис. 10
Решение
Обозначим через х величину угла BAD, а через h ширину досок, тогда
АВ = ВС = CD = h, AE = hcosx, AD = h + 2hcosx, BE = hsinx.
Желоб представляет собой призму, основанием
которой служит трапеция ABCD, а высота равна длине
сбиваемых досок. Обозначив длину досок через l,
найдем объем желоба. V(x) = l h2 (1+cosx)sinx.
Требуется узнать при каком значении х из
интервала (0; ![]() ) функция V принимает наибольшее
значение.
) функция V принимает наибольшее
значение.
Найдем производную функции V:
V' = l h2(cosx(l + cosx) –
sin2x) = l h2 (2cos2x + cosx – 1) =2 l
h2 (cosx – ![]() )(cosx +1),
)(cosx +1),
замечаем, что на
рассматриваемом интервале производная существует
и обращается в нуль только при х =![]() ,
причем при 0 < х <
,
причем при 0 < х < ![]() производная положительна, а при
производная положительна, а при ![]() < х <
< х < ![]() отрицательна.
Значит, функция V достигает своего наибольшего
значения на интервале (0;
отрицательна.
Значит, функция V достигает своего наибольшего
значения на интервале (0; ![]() ) при х =
) при х = ![]() .
.
Зная оптимальное значение x, найдем искомое
значение ![]() :
:![]() =
= ![]() .
.
Ответ: ![]() =
= ![]()
Задача 8
Каким должно быть отношение диаметра основания к высоте закрытой цилиндрической цистерны, чтобы при заданном объеме на изготовление цистерны шло как можно меньше материала?
Решение
Пусть r – радиус основания, V – объем цистерны,
тогда ее высота равна ![]() , а полная поверхность S(r) = 2(
, а полная поверхность S(r) = 2(![]() г2
+
г2
+ ![]() ).
Требуется узнать, при каком r из промежутка
(0;+
).
Требуется узнать, при каком r из промежутка
(0;+![]() ),
функция S достигает наименьшего значения.
),
функция S достигает наименьшего значения.
Найдем производную: S' (r) = 2(2![]() =
= 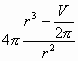 .
.
Замечаем, что производная всюду на
рассматриваемом интервале существует и
обращается в нуль только в точке ![]() =
= ![]() причем
S'(r) < 0 при 0 <
причем
S'(r) < 0 при 0 < ![]() <
< ![]() и S'(x) > 0 при
и S'(x) > 0 при ![]() >
> ![]() .
.
Функция S при r = r0 достигает наименьшего
значения. При величине радиуса г = г0 высота
цистерны h0 = ![]() =
= ![]() , т.е. высота цилиндра должна быть
равна его диаметру, а отношение равно 1.
, т.е. высота цилиндра должна быть
равна его диаметру, а отношение равно 1.
Ответ: 1.
Литература
- Журнал “Математика в школе” № 6 – 1980 г. Статья “ Применение производной в практической деятельности”, автор В.Е. Львов.
- Журнал “ Математика в школе” № 6 – 1977г. Статья “ Несколько простых прикладных задач”, автор Я.Е.Жак.
- Книга для учителя “Прикладные задачи по алгебре”, М: “ Просвещение” – 1999 г., автор Ю.Ф.Фоминых.