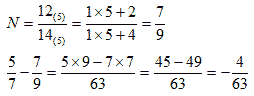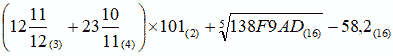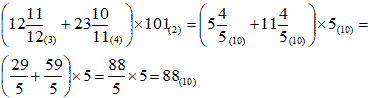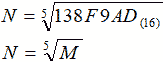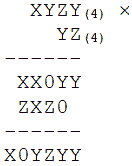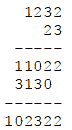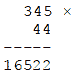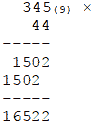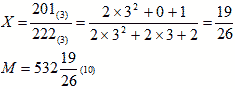Профильное предметное обучение учащихся предполагает углубленный уровень решения задач. В данной работе предлагается набор задач, которые могут быть использованы в классе с профильным изучением информатики с целью дополнительной, расширенной подготовки. Задачи представляют три основные направления, ставшие уже классическими: арифметическое, логическое и алгоритмическое. Начнем, как обычно, с арифметики.
1. Арифметические операции над числами в недесятичных системах счисления
Учащийся должен хорошо понимать, что такое число, уметь работать с числами в позиционных системах счисления с недесятичным основанием. Просто переводить числа из одной системы счисления в другую уже не достаточно для сдачи ЕГЭ по информатике. Интерес представляют задачи специального вида. Некоторые разновидности таких задач представлены в этом наборе.
ЗАДАЧА 1. Даны два действительных числа в системах счисления с различными основаниями. Сравнить между собой значения данных чисел (если числа не равны, то определить, какое из них больше).
M = 0,10(110)(2)
Основная трудность решения заключается в том, что первое число представляет собой бесконечную периодическую двоичную дробь. Прежде чем сравнивать числа между собой, требуется записать это число в форме обыкновенной дроби. Для устранения бесконечной периодической части можно использовать очевидные арифметические преобразования.
Обозначим исходное число как М. Тогда:
100 M = 10,(110)
100000 M = 10110,(110)
Вычитая меньшее число из большего, получим:
10110,(110) – 10,(110) = 10100
100000 M – 100 M = 11100 M
Таким образом:
11100 M = 10100
Отсюда можно найти значение М в форме обыкновенной дроби и перевести его в десятичную систему счисления.
Теперь достаточно перевести второе число в десятичную систему счисления и сравнить числа между собой. Для сравнения обыкновенных дробей достаточно определить значение разности между ними.
M - N < 0
Разность между первым и вторым числами меньше нуля, следовательно первое число меньше второго.
Ответ: M < N
ЗАДАЧА 2. Вычислить значение числового выражения. Результат записать в четверичной системе счисления. Число под знаком корня является пятой степенью целого положительного числа.
Решение этой задачи, как и всех задач вычислительного типа, сводится к арифметическим операциям над недесятичными числами, целыми и дробными. В случае большого размера выражения вычисления удобнее выполнять по частям.
Для левой части выражения вычисления можно выполнить в десятичной системе счисления.
Мы получили десятичное число 88. В шестнадцатиричной системе счисления это число имеет запись 58=5×16+8. Вычитая шестнадцатиричную дробь из полученного числа, получим:
Теперь необходимо найти значение корня пятой степени из шестнадцатиричного числа.
Известно, что значение корня является целым положительным числом и это упрощает необходимые рассуждения. Сначала попробуем определить границы для искомого значения, чтобы максимально сократить область поиска.
( 10(16) )5 = 100000(16) < M
( 10(16)) )5 = 10000000000(16) > M
Мы видим, что пятая степень наименьшего двухразрядного шестнадцатиричного числа меньше М. С другой стороны, пятая степень наименьшего трехразрядного шестнадцатиричного числа больше М. Таким образом, искомое значение может быть только двухразрядным числом.
N = XY(16) = 16X + Y
Попробуем определить значение первой цифры (X). Возведем в пятую степень шестнадцатиричное число 20 и сравним полученное значение с М. Для чисел, заканчивающихся нулем сделать это не сложно.
20 × 20=400
400 × 20=8000
8000 × 20=100000
100000 × 20=2000000 > M
Полученное значение больше М. Это значит, что значение первой цифры N уже определено: она равна 1. Таким образом, искомое число начинается с единицы и имеет следующий вид:
N = 1Y(16) = 16 + Y
Теперь надо найти значение цифры Y. Очевидно, что при умножении четных цифровых разрядов могут получаться только четные значения. В последнем разряде числа М расположена нечетная цифра D. Следовательно, значение младшей цифры в числе N может быть только нечетным. Значение 1 можно исключить сразу, т.к. единица при умножении дает в последнем разряде только саму себя.
Y = 2n + 1; Y ǂ 1; Y ϵ { 3, 5, 7, 9, B, D, F }
Посмотрим, как ведут себя нечетные цифры при возведении числа в степень. Нас интересуют только последние цифровые разряды, поэтому выполнять умножение в полном объеме не обязательно. Для цифры 3 покажем результаты полностью, для остальных укажем только цифры в последних разрядах произведений.
Вторая степень: 3 × 3 = 9
Третья степень: 9 × 3 = *B
Четвертая степень: 1B × 3 = *1
Пятая степень: 51 × 3 = *3
Начиная с шестой степени цифры в последних разрядах образуют периодическую последовательность вида: ( 9, B, 1, 3, … ). Похожие результаты получаются для всех нечетных цифр от 3 до F.
5: 9, D, 1, 5, …
7: 1, 7, …
9: 1, 9, …
B: 9, 3, 1, B, …
D: 9, 5, 1, D, …
F: 1, F, …
Таким образом, только две цифры дают значение D в последних разрядах своих степеней, при этом только для цифры D это значение образуется именно для пятой степени. Это значит, что последняя цифра числа найдена: Y = D.
Итак, число N найдено.
Теперь мы можем выполнить последнюю операцию вычитания и перевод результата в четверичную систему счисления.
1D(16) – 0,2(16) = 1C,E(16)
1C,E(16) = 11100,111(2)
11100,111(2) = 130,32(4)
Ответ: 130,32(4)
ЗАДАЧА 3. Дана запись операции умножения двух целых чисел в системе счисления с основанием четыре. При этом все цифровые разряды чисел, кроме нулевых, не известны и обозначены буквами латинского алфавита X,Y,Z. Определить значения данных чисел (цифровые разряды).
Для четверичного основания найти решение задачи не очень сложно. Цифра 0 исключается. Следовательно, для неизвестных значений цифровых разрядов остаются только три допустимых значения: 1, 2, 3. Таким образом, общее количество возможных вариантов равно 6 = 3! (факториал 3). При этом нет необходимости рассматривать все варианты умножения в полном объеме. Две младшие цифры в первом частичном произведении являются равными. Если это не так, то вариант можно отбрасывать.
| 1 | 2 |
3 |
4 |
5 |
6 |
1232 |
1323 |
2131 |
2313 |
3121 |
3212 |
Из представленной таблицы видно, что необходимый результат дает только один вариант: X=1, Y=2, Z=3. Для полной уверенности подставим эти значения в текст примера и убедимся в правильности решения.
Ответ: X=1; Y=2; Z=3; Первое число 1232; Второе число 23.
ЗАДАЧА 4. Определить основания систем счисления X и Y, для которых выполняются все следующие условия:
1) 234(X) < 165(Y)
2) 543(X)) + 22(X) = 565(X)
3) 345(Y) × 44(Y) = 16522(Y)
В подобных задачах самое главное, это как можно больше ограничить область допустимых значений для неизвестных величин. В данном случае к данным условиям можно сразу добавить еще три:
X > 6; Y > 6; Y > X;
Основания не могут быть меньше 7, потому что в записи чисел наибольшей цифрой является шесть. Третье неравенство является прямым следствием первого условия: трехзначное число, начинающееся с 1, может быть больше другого трехзначного числа, начинающегося с двойки, только в том случае, когда оно задано в системе счисления с большим основанием.
Дальше можно рассуждать следующим образом. Уравнение для X не дает нам однозначного решения: оно образует тождество для множества значений X:
543(7) + 22(7) = 565(7)
543(8) + 22(8) = 565(8)
543(9) + 22(9) = 565(9)
543(10) + 22(10) = 565(10)
…
Следовательно, надо перейти к анализу условий, заданных для Y.
Произведение 5 на 4 равно 20. Если при умножении в системе с основанием Y получено число 20, которое в этой системе счисления имеет запись вида N2, то полученный результат можно записать следующим образом:
NY + 2 = 20
NY= 18
Число 18 делится без остатка только на 1, 3, 6, 9, 18. Если учесть при этом, что Y>6, то возможными решениями остаются только 9 и 18. Но решение Y=18 не подходит, потому что в этом случае следующее умножение 4 на 4 с учетом единицы переноса дает значение 17 и следующий по порядку разряд произведения не может быть равен двум. Напротив, умножение по основанию 9 дает требуемый результат:
Следовательно, решение для Y найдено: Y = 9.
Теперь надо найти решение для X. Для X остаются возможными два значения: X=7; X=8; Чтобы выбрать единственное, остается рассмотреть данное нам неравенство.
Запишем числа в виде алгебраических функций от X и Y.
2X2 + 3X + 4 < Y2 + 6Y + 5
После подстановки значения Y=9 и несложных преобразований получим:
2X2 + 3X + 4 < 92 + 6 × 9 + 5
2X2 + 3X < 81 + 54 + 5 - 4
2X2 + 3X < 136
X(2X+3) < 136
Допустимых значений для X всего два, поэтому решение неравенства можно найти с помощью простой подстановки:
7(14+3) = 119 < 136
8(16+3) = 152 > 136
Значение X=8 нарушает неравенство. Следовательно, единственным допустимым значением для X является X=7. Задача решена.
Ответ: X=7; Y=9.
ЗАДАЧА 5. При сложении трех неизвестных чисел в двенадцатиричной системе счисления выполняется следующее равенство:
XYZ + ZY + Z = ZXY
Число X возвели в степень N=YZ и результат записали в шестнадцатиричной системе счисления. Определить значение последней цифры в записи полученного шестнадцатиричного числа.
Первое, что требуется для решения задачи, это найти неизвестные значения цифровых разрядов. Начнем с исследования суммы последних разрядов.
При сложении трех цифр образуется число, которое заканчивается на цифру Y. Если первый разряд этого числа равен 1, то можно составить уравнение и получить возможное значение для Z.
Z + Y + Z = 1Y
2Z + Y = 12 + Y
2Z = 12
Z = 6;
Никаких других решений для Z нет. Если предположить, что старший разряд суммы равен 2, то мы получим следующее:
Z + Y + Z = 2Y
2Z + Y = 24 + Y
2Z = 24
Отсюда Z=12, что невозможно в c/c с основанием 12;
Таким же образом, путем анализа ситуации при сложении средних разрядов, получим решение для Y и X. Не забудем, что здесь необходимо учесть единицу переноса из младшего разряда суммы. На основе анализа сложения в средних разрядах получим:
Y + 6 + 1 = 1X
Y + 7 = 12 + X
Y = X + 5
При этом в старшем разряде суммы разряд Z=6 может образоваться только при сложении цифры X и единицы переноса.
X + 1 = 6
X = 5
Соответственно для цифры Y имеем следующее:
Y = 5 + 5 = A
Проверим значения разрядов путем подстановки.
Теперь можно приступить ко второй части задания. Показатель степени, в которую возвели число X равен:
N = YZ = A6 = 106 = 1000000(10)
Чтобы ответить на вопрос, какая цифра будет в последнем разряде шестнадцатиричной степени, надо понять, как ведет себя число 5 при возведении в степень в шестнадцатиричной системе счисления. При этом нас интересуют только те значения цифр, которые образуются в последних разрядах.
Первая степень: 5
Вторая степень: 5 × 5= 19
Третья степень: 5 × 5 × 5 = *D
Четвертая степень: 5 × 5 × 5 × 5 = *1
Дальше образуется период с длиной 4:
( 5; 9; D; 1 )
Одинаковые цифры образуются в последнем разряде степени для всех показателей степени, которые имеют одинаковые остатки при делении на длину периода, т.е. на четыре. Например, на цифру 1 заканчиваются все степени с показателями, которые кратны четырем: 4, 8, 12, 16, и т.д. Один миллион делится на четыре без остатка. Следовательно, последняя цифра в миллионной степени шестнадцатиричного числа равна 1.
Ответ: Последняя цифра в записи полученного шестнадцатиричного числа равна 1.
ЗАДАЧА 6. Дана периодическая дробь в троичной системе счисления (M). Записать число в системе счисления с основанием шестнадцать. Определить значение цифры, которая находится в полученном шестнадцатиричном числе в позиции с троичным номером N=201211221(3) после запятой.
M = 201201,(201)(3)
Переведем данное число в шестнадцатиричную систему счисления. Сначала выполним перевод из троичной системы в десятичную, потом – из десятичной в шестнадцатиричную. Для целой части числа используем обычные алгоритмы преобразования, для дробной части воспользуемся методом, который мы уже применяли для устранения периодической части дроби (см. решение задачи №1).
Переводим целую часть числа в десятичную систему счисления.
201201(3) = 2 × 35 + 0 + 1 × 33 + 2 × 32 + 0 + 1 = 2 × 243 + 27 + 18 + 1 = 486 + 27 + 18 + 1 = 532(10)
Переводим дробную часть числа в десятичную систему счисления.
X = 0,(201)(3)
1000X = 201,(201)(3)
201,(201) (3) - 0,(201)(3) = 201
1000X - X = 222X
Теперь выполним перевод целой и дробной частей числа в шестнадцатиричную систему счисления.
532 : 16 = 33; остаток = 4;
33 : 16 = 2; остаток = 1;
2 : 16 = 0; остаток = 2;
532(10) = 214(16)
19 : 16 = 1; остаток = 3;
1 : 16 = 0; остаток = 1;
19(10) = 13(16)
26 : 16 = 1; остаток = A;
1 : 16 = 0; остаток = 1;
26(10) = 1A(16)
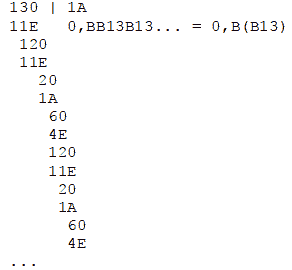
Мы получили число в форме обыкновенной шестнадцатиричной дроби. Для того, чтобы получить запись числа с шестнадцатиричной запятой, надо разделить числитель обыкновенной дроби на ее знаменатель.
Мы получили бесконечную периодическую дробь в шестнадцатиричной системе счисления.
M = 214,B(B13)(16)
Первая цифра после запятой не входит в состав периода. Поэтому удобнее нумеровать цифры, начиная со второй цифры после запятой. Другими словами, нам надо найти значение цифры с номером S=N-1 от начала периодической части числа.
S = N-1 = 201211221(3) - 1 = 201211220(3)
Значения цифр в периодической части числа повторяются через каждые три разряда. Это значит, что остаток от деления номера цифры на три позволяет нам определить значение цифры с любым номером. Если число в троичной системе счисления заканчивается на цифру 0, то это значит, что данное число делится на 3 без остатка.
Но если номер цифры делится на три без остатка, то эта цифра занимает третье место в составе периода. Третья цифра в периоде дроби это цифра три.
Ответ: Цифра с троичным номером 201211221 после запятой в шестнадцатиричной записи троичного числа 201201,(201) равна 3.
2. Решение логических задач с использованием аппарата алгебры логики