Эпитет урока:
Окружность – душа геометрии.
Познайте окружность, и вы не только познаете душу
геометрии, но и возвысите душу свою
(К.Птолемей)
Цели:
- Систематизировать ранее полученные знания по решению планиметрических задач на окружности, вписанные в многоугольник и описанные около многоугольника;
- Углубление содержания базового курса;
- Получить дополнительную подготовку к ЕГЭ;
- Развитие устойчивого интереса учащихся к изучению математики;
- Развитие логического мышления учащихся, обогащение и расширение математического кругозора учащихся.
На доске 2 плаката:
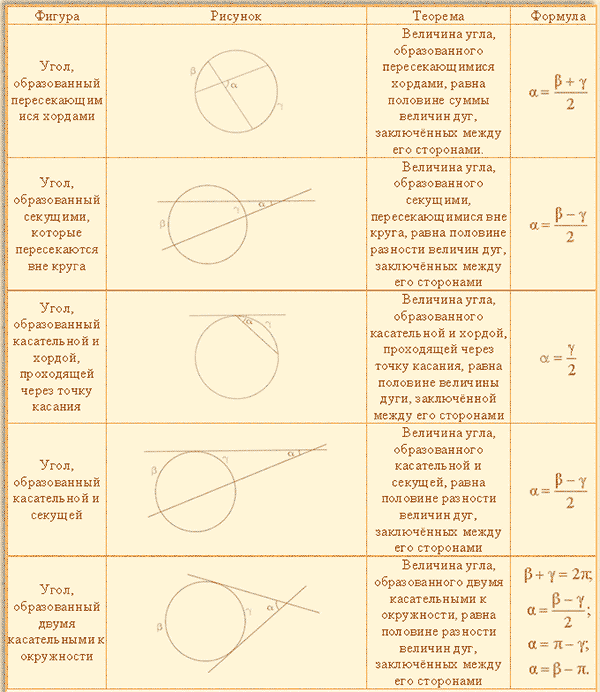
Теоремы о вписанных и центральных углах

Теоремы об углах, образованных хордами, касательными и секущими
Устные упражнения
Задача 1 (см.слайды 6-7)
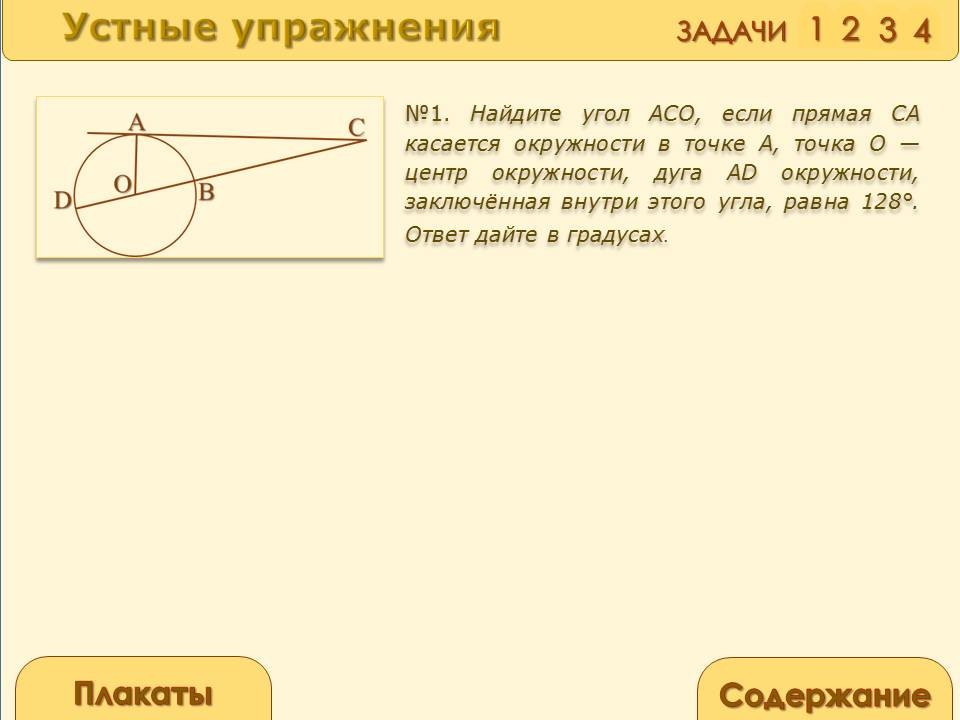
Найдите угол ACO, если прямая CA касается окружности в точке A, точка O — центр окружности, дуга AD окружности, заключённая внутри этого угла, равна 128°. Ответ дайте в градусах.
Решение:
Угол между касательной и радиусом, проведённым
в точку касания, прямой: ![]() OAC=90°.
Центральный угол DOA равен угловой величине
дуги, на которую он опирается, то есть ?DOA=?DA=128о.
Внешний угол треугольника равен сумме двух
углов, не смежных с ним,
OAC=90°.
Центральный угол DOA равен угловой величине
дуги, на которую он опирается, то есть ?DOA=?DA=128о.
Внешний угол треугольника равен сумме двух
углов, не смежных с ним,
![]() DOA =
DOA = ![]() OAC +
OAC + ![]() ACO,
ACO, ![]() ACO=128о – 90о=38о.
ACO=128о – 90о=38о.
Ответ: 38о.
Задача 2 (см.слайды 8-9)
Хорда AB стягивает дугу окружности в 104°. Найдите угол ABC между этой хордой и касательной к окружности, проведённой через точку B. Ответ дайте в градусах.
Решение.
Угол между хордой и касательной к окружности,
проведённой из конца хорды, равен половине
угловой величины дуги, которую стягивает эта
хорда. ![]() CBA=0,5*AB=0,5*104о=52о.
CBA=0,5*AB=0,5*104о=52о.
Ответ: 52о.
Задача 3 (см.слайды 10-11)
Через концы A и B дуги окружности в 56° проведены касательные AC и BC. Найдите угол ACB. Ответ дайте в градусах.
Решение.
![]() OBC=
OBC=![]() OAC=90?, так как касательная
перпендикулярна радиусу, проведённому в точку
касания.
OAC=90?, так как касательная
перпендикулярна радиусу, проведённому в точку
касания. ![]() BOA=BA=56о
(центральный угол опирается на дугу 56°). В
четырёхугольнике OBCA сумма углов равна 360°.
BOA=BA=56о
(центральный угол опирается на дугу 56°). В
четырёхугольнике OBCA сумма углов равна 360°. ![]() ACB=360о–90о–90о–56о=124о.
ACB=360о–90о–90о–56о=124о.
Ответ: 124о.
Задача 4 (см.слайды 12-13)
Центральный угол на 54° больше острого вписанного угла, опирающегося на ту же дугу окружности. Найдите вписанный угол. Ответ дайте в градусах.
Решение.
Центральный угол в два раза больше вписанного угла, опирающегося на ту же дугу. Если он на 54° больше вписанного угла, то вписанный угол равен 54°.
Ответ: 54о.
Проверка домашнего задания
Задача (см.слайды 14-15)
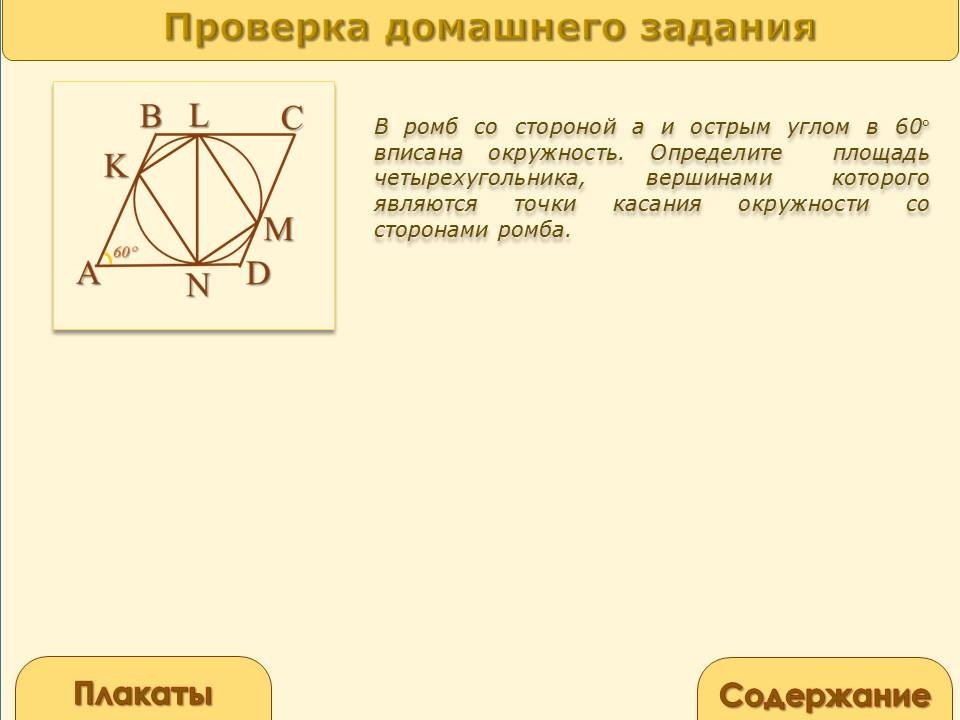
В ромб со стороной а и острым углом в 60° вписана окружность. Определите площадь четырехугольника, вершинами которого являются точки касания окружности со сторонами ромба.
Решение:
Радиус вписанной в ромб АВСD окружности R=![]() ; так как
; так как ![]() KLMN –
прямоугольник, так как его углы, опираются на
диаметр окружности.
KLMN –
прямоугольник, так как его углы, опираются на
диаметр окружности.
S(KLMN)=MN![]() ;
где MN=R (катет, лежащий против угла в 30
;
где MN=R (катет, лежащий против угла в 30![]() ); LM=R
); LM=R![]()
S=![]() =
= ![]() .
.
Ответ: ![]()
Работа по теме урока
Тема урока актуальная и важная, поскольку встречается на ГИА (ОГЭ и ЕГЭ). Сегодня на уроке рассмотрим геометрические конфигурации, наиболее часто встречающиеся в задачах: касающиеся окружности, пересекающиеся окружности, вписанные и описанные окружности треугольника и четырехугольника и т.д., способы нахождения различных элементов геометрических фигур - медиан, высот, биссектрис треугольника, радиусов вписанных и описанных окружностей и т.д.
Задача 1 (см.слайды 16-17)
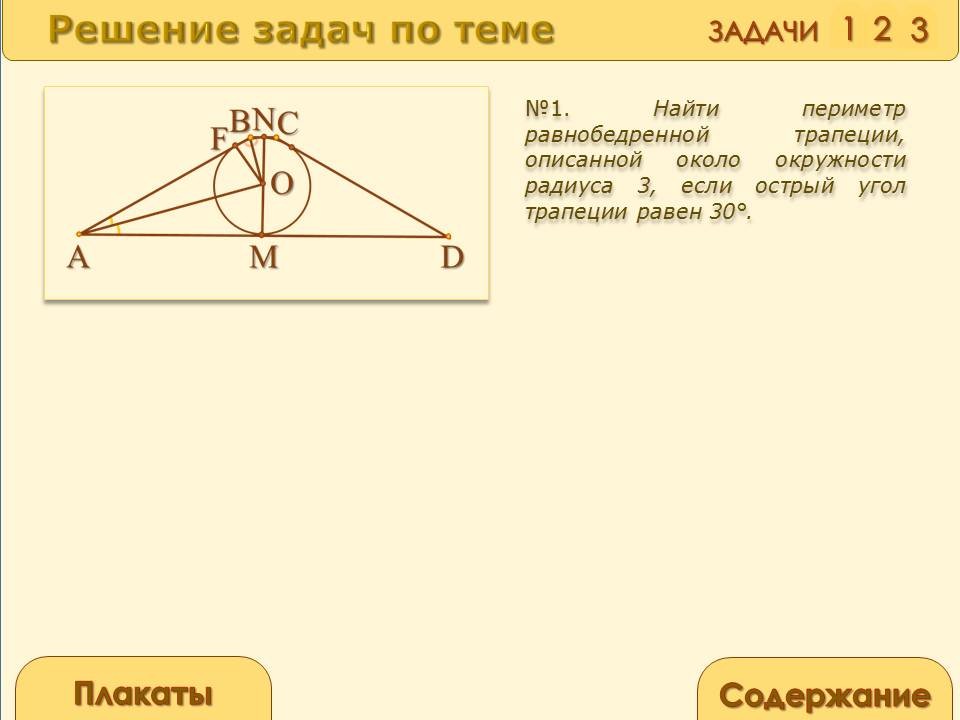
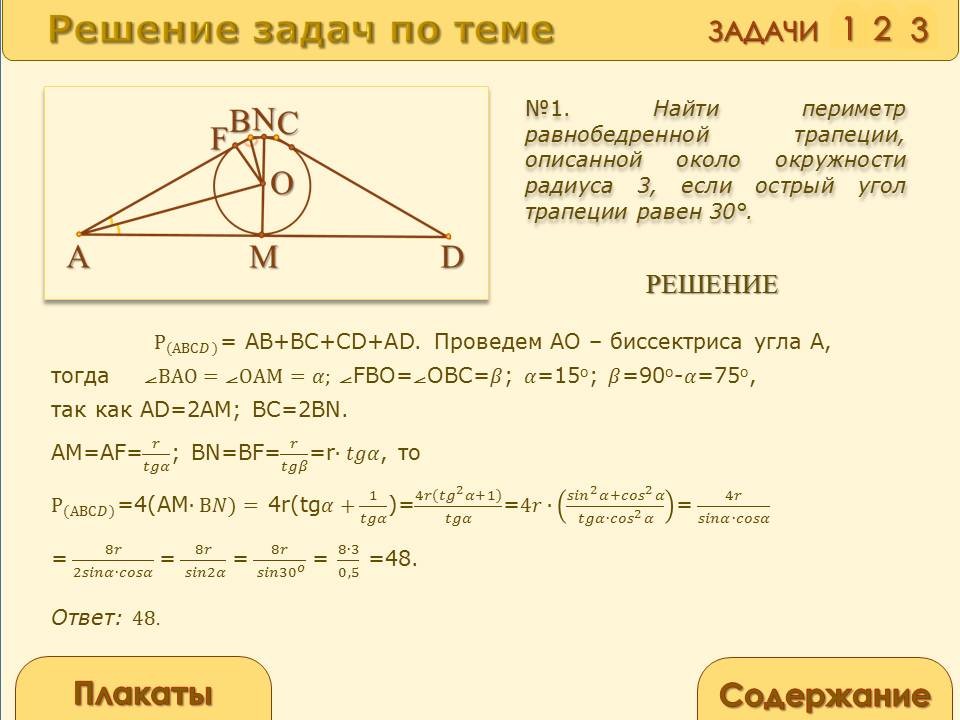
Найти периметр равнобедренной трапеции, описанной около окружности радиуса 3, если острый угол трапеции равен 30о.
Решение:
![]() =
АВ+ВС+СD+AD. Проведем АО – биссектриса угла А, тогда
=
АВ+ВС+СD+AD. Проведем АО – биссектриса угла А, тогда![]()
![]() FBO=
FBO=![]() OBC=
OBC=![]() ;
; ![]() =15о;
=15о; ![]() =90о-
=90о-![]() =75о, так как
АВ=2АМ; ВС=2ВN.
=75о, так как
АВ=2АМ; ВС=2ВN.
АМ=АF=![]() ;
ВN=BF=
;
ВN=BF=![]() =r
=r![]() , то
, то
![]()
Ответ: 48
Задача 2 (см.слайды 18-19)
В окружности проведены хорды АВ=![]() и АС=2
и АС=2![]() ,
, ![]() ВАС=60о. Хорда АD – биссектриса
ВАС=60о. Хорда АD – биссектриса ![]() ВАС. Найти длину хорды АD
ВАС. Найти длину хорды АD![]()
Решение:
Пусть АD=х. АВСD – вписанный четырехугольник; АD-
биссектриса, тогда ![]() ВАD =
ВАD = ![]() DАС – вписанные углы в
окружность, значит, ВD = DС, тогда хорды,
стягивающие эти дуги, также равны. Пусть ВD = DC = а.
DАС – вписанные углы в
окружность, значит, ВD = DС, тогда хорды,
стягивающие эти дуги, также равны. Пусть ВD = DC = а.
![]() ВАD =
ВАD =![]() DАС=30о. По теореме косинусов из
DАС=30о. По теореме косинусов из ![]()
![]() найдем а:
найдем а:
ВD2=а2=АВ2+АD2-2АВ*АD![]() cos30о;
cos30о;
ВD2=а2= 3+х2-2![]() х
х![]() = х2-3х+3 (1)
= х2-3х+3 (1)
DC2=а2=12+х2-2![]() х
х![]() = х2-6х+12 (2); из (1) – (2) получим
= х2-6х+12 (2); из (1) – (2) получим
3х-9=0,
х=3.
АD=3.
Ответ: 3.
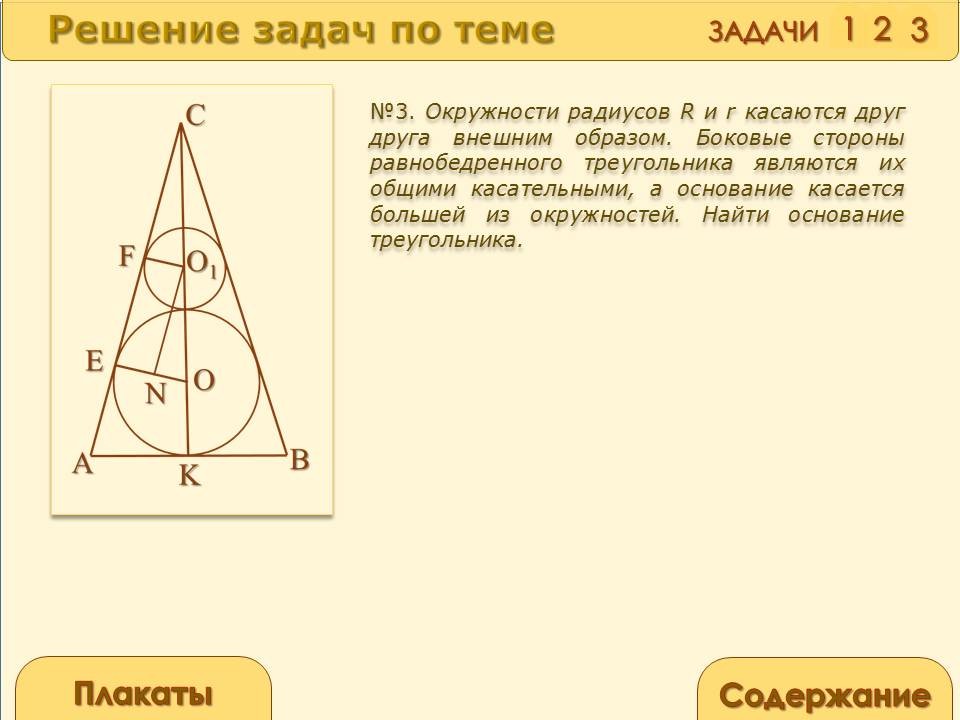
Задача 3. (см.слайды 20-22)
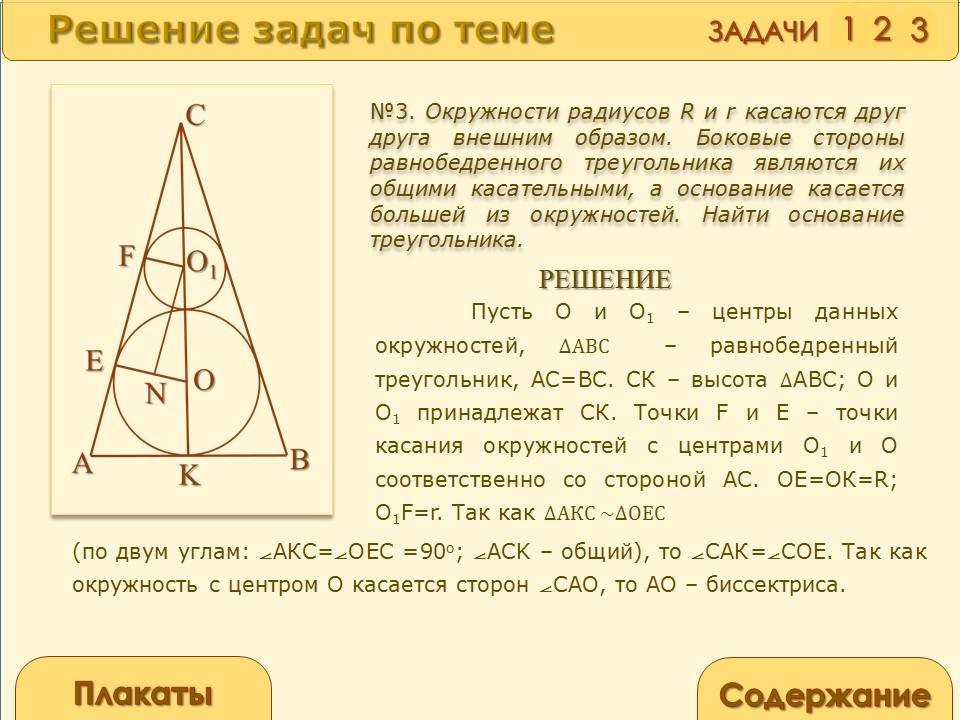
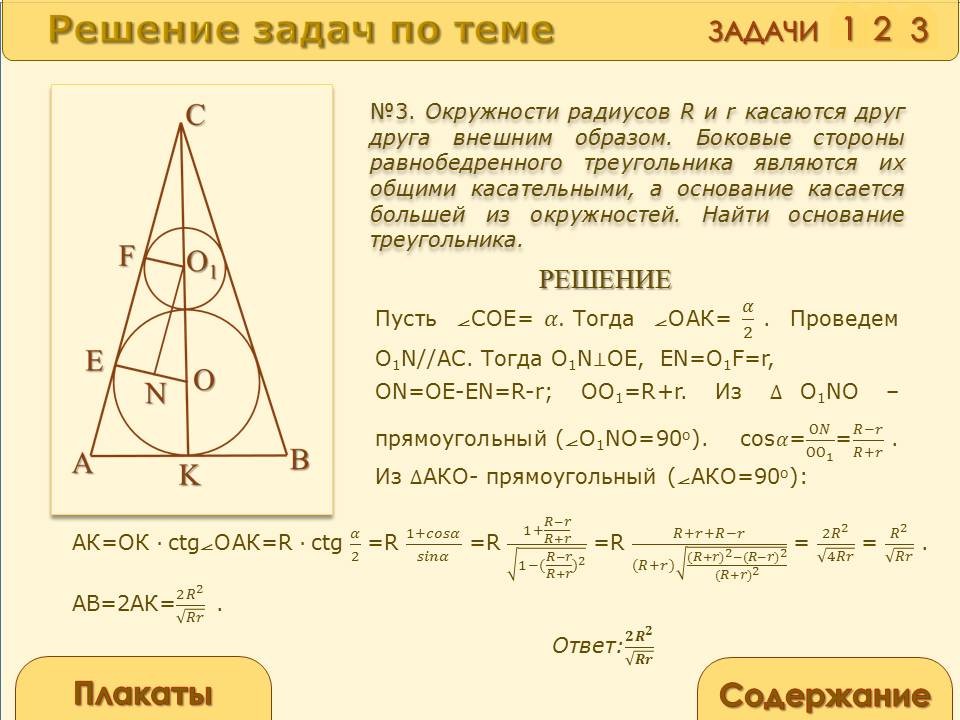
Окружности радиусов R и r касаются друг друга внешним образом. Боковые стороны равнобедренного треугольника являются их общими касательными, а основание касается большей из окружностей. Найти основание треугольника.
Решение:
О и О1 – центры данных окружностей, ![]() –
равнобедренный треугольник, АС=ВС. СК – высота
–
равнобедренный треугольник, АС=ВС. СК – высота ![]() АВС; О и О1
принадлежат СК. Точки F и E – точки касания
окружностей с центрами О1 и О
соответственно со стороной АС. ОЕ=ОК=R; О1F = r.
Так как
АВС; О и О1
принадлежат СК. Точки F и E – точки касания
окружностей с центрами О1 и О
соответственно со стороной АС. ОЕ=ОК=R; О1F = r.
Так как ![]() АКС
АКС
![]() (по
двум углам:
(по
двум углам: ![]() АКС=
АКС= ![]() ОЕС =90о;
ОЕС =90о; ![]() С – общий), то
С – общий), то ![]() САК=
САК=![]() СОЕ.
СОЕ.
Так как окружность с центром О касается сторон ![]() САО, то АО – биссектриса.
Пусть
САО, то АО – биссектриса.
Пусть ![]() СОЕ=
СОЕ=![]() . Тогда
. Тогда ![]() ОАК=
ОАК=![]() . Проведем О1N//АС. Тогда О1N
перпендикулярен ОЕ, ЕN=О1F=r, ОN=ОЕ-ЕN=R-r; ОО1=R+r.
Из
. Проведем О1N//АС. Тогда О1N
перпендикулярен ОЕ, ЕN=О1F=r, ОN=ОЕ-ЕN=R-r; ОО1=R+r.
Из ![]() О1NО
– прямоугольный (
О1NО
– прямоугольный (![]() О1NО=90о).
cos
О1NО=90о).
cos![]() =
=![]() =
=![]() . Из
. Из ![]() АКО- прямоугольный (
АКО- прямоугольный (![]() АКО=90о): АК=ОК*ctg?ОАК=R
АКО=90о): АК=ОК*ctg?ОАК=R![]() ctg
ctg![]() =R
=R![]() =
=
=R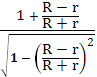 =R
=R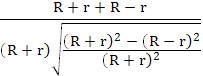 =
=![]() =
=![]() . АВ=2АК=
. АВ=2АК=![]() .
.
Ответ: ![]() .
.
Работа творческой группы
Эпиграф творческой группы:
"Математика открывает свои тайны только тому,
кто занимается ею с чистой любовью,
ради ее собственной красоты."
Архимед
Руководитель творческой группы:
Наша творческая группа на своих заседаниях рассмотрела труды Архимеда, связанные с окружностью.
Труды Архимеда были сделаны свыше 2000 лет назад и опередили свое время как минимум на 17 веков. Множество его трудов пропало без вести — но даже того, что осталось, вполне достаточно, чтобы поставить Архимеда в один ряд с Ньютоном, Гауссом, да Винчи. Благодаря этому его можно с полным правом назвать одним из величайших гениев человечества.
Задача 1 (см.слайды 25-26)
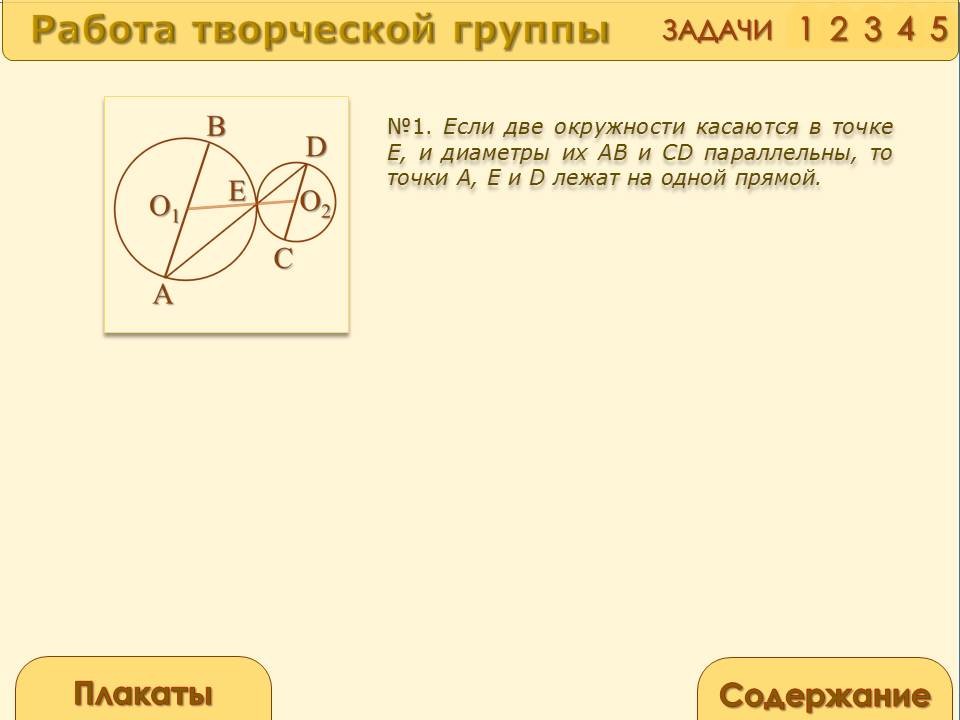
Если две окружности касаются в точке Е, и диаметры их АВ и CD параллельны, то точки А, Е и D лежат на одной прямой.
Решение:
Рассмотрим случай, когда окружности касаются внешним образом. Соединим центры окружностей отрезком О1O2, который пройдет через точку Е. Углы АО1Е и DO2E равны как накрест лежащие при параллельных прямых АВ и CD. Треугольники АО1Е и DO2E равнобедренные, имеют равные углы при вершинах, следовательно, все четыре угла при основаниях треугольников равны между собой. Значит, по разные стороны от прямой OгО2, отложены равные углы О1ЕА и O2ED, откуда и следует, что точки А, Е и D лежат на одной прямой.
Задача 2 (см.слайды 27-28)
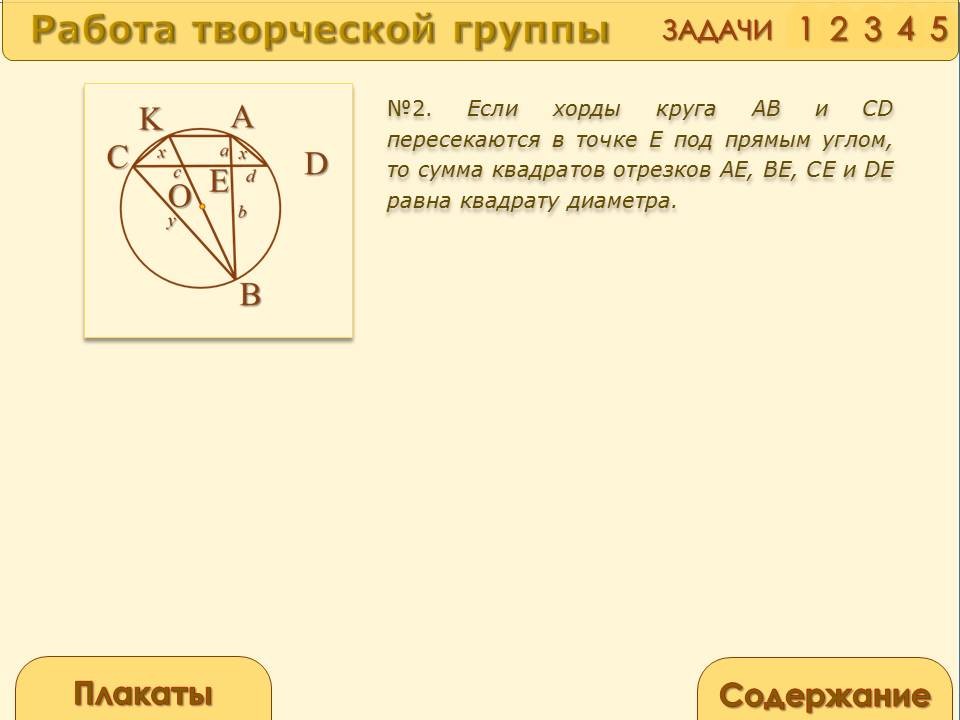
Если хорды круга АВ и CD пересекаются в точке Е под прямым углом, то сумма квадратов отрезков АЕ, BE, СЕ и DE равна квадрату диаметра.
Решение:
Пусть а, b, с, d - данные отрезки хорд АВ и CD . Пусть АD = х, ВС = у. Тогда по теореме Пифагора для треугольника AED:
x2 =a2+d2 (1)
А по теореме Пифагора для треугольника ВЕС:
y2=b2+c2 (2)
Проведем АК ¦ CD. Тогда ВК= 2R – диаметр (так как ![]() KAB = 90°).
KAB = 90°).
СКАD - равнобокая трапеция, поскольку в
окружность можно вписать только равнобокую
трапецию, и СК = AD = x. ![]() KCB = 90°
(опирается на диаметр). Тогда по теореме Пифагора
для треугольника КСВ имеем:
KCB = 90°
(опирается на диаметр). Тогда по теореме Пифагора
для треугольника КСВ имеем:
x2+y2=4R2
Воспользовавшись равенствами (1) и (2), получаем требуемое:
a2+b2+c2+d2=4R2
Задача 3 (см.слайды 29-30)
Если к окружности из внешней точки провести секущую через центр, а другую так, чтобы внешний отрезок равнялся радиусу окружности, то угол между секущими будет измеряться одной третью большей из дуг, заключенной между его сторонами.
Решение:
Пусть данные секущие будут АВ и АС (АС
пересекает окружность в точке D), а угол между
ними равен a. Соединим точку D с точками О и В.
Покажем, что угловая мера дуги ВС будет Зa.
Угол AOD равен a и является внешним для
треугольника DOB, поэтому ![]() ODB=
ODB=
![]() OBD = a/2 . Угол BDC —
внешний для треугольника BDA, поэтому
OBD = a/2 . Угол BDC —
внешний для треугольника BDA, поэтому ![]() BDC= a + a/2 = 3a/2.
Поскольку
BDC= a + a/2 = 3a/2.
Поскольку ![]() BDC измеряется
половиной дуги ВС, то мера дуги BC составляет 3?.
BDC измеряется
половиной дуги ВС, то мера дуги BC составляет 3?.
Задача 4 (см.слайды 31-32)
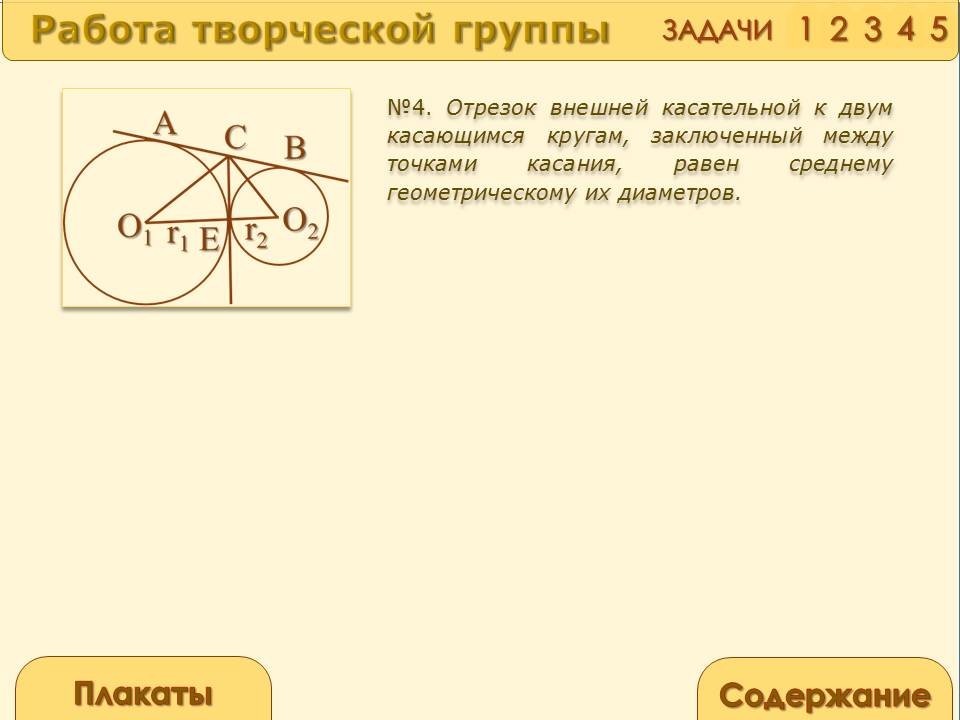
Отрезок внешней касательной к двум касающимся кругам, заключенный между точками касания, равен среднему геометрическому их диаметров.
AB2=d1d2
Решение:
Проведем через точку Е касания двух
окружностей их общую касательную ЕС. Тогда АС=СЕ
=СВ как отрезки общих касательных. Поскольку CO1
и СO2— биссектрисы углов АСЕ и ВСЕ, то угол
между ними равен 90°. Из прямоугольного
треугольника О1СО2: СЕ = ![]() и
и ![]() .
.
Задача 5 (см.слайды 33-34)
На отрезке АС взята точка D, и на отрезках AC, AD и CD
как на диаметрах построены полуокружности.
Закрашенную фигуру Архимед назвал “арбелон” (![]() — скребок,
скорняжный нож). Восстановим из точки D
перпендикуляр BD. Тогда площадь арбелона равна
площади круга с диаметром BD.
— скребок,
скорняжный нож). Восстановим из точки D
перпендикуляр BD. Тогда площадь арбелона равна
площади круга с диаметром BD.
Решение:
Пусть радиус большей полуокружности равен r1, а радиус меньшей — r2. Тогда площадь арбелона равна
![]()
Из прямоугольного треугольника ABC имеем: ![]() . Площадь круга с
диаметром BD будет равна
. Площадь круга с
диаметром BD будет равна ![]() , что и требовалось доказать.
, что и требовалось доказать.
Домашнее задание
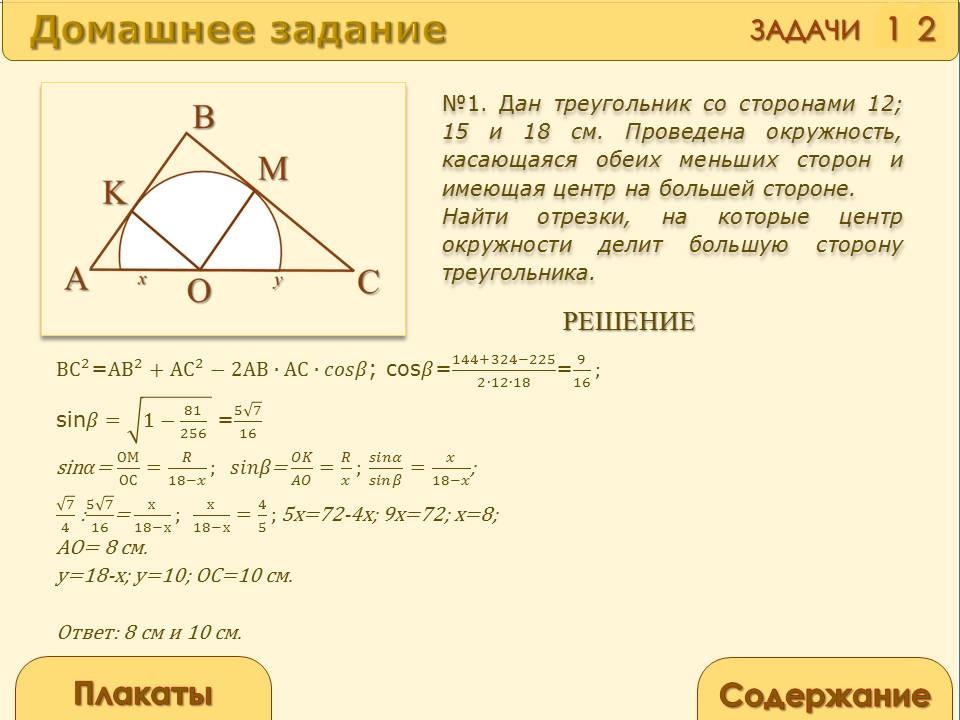
Задача 1 (см.слайды 35-37)
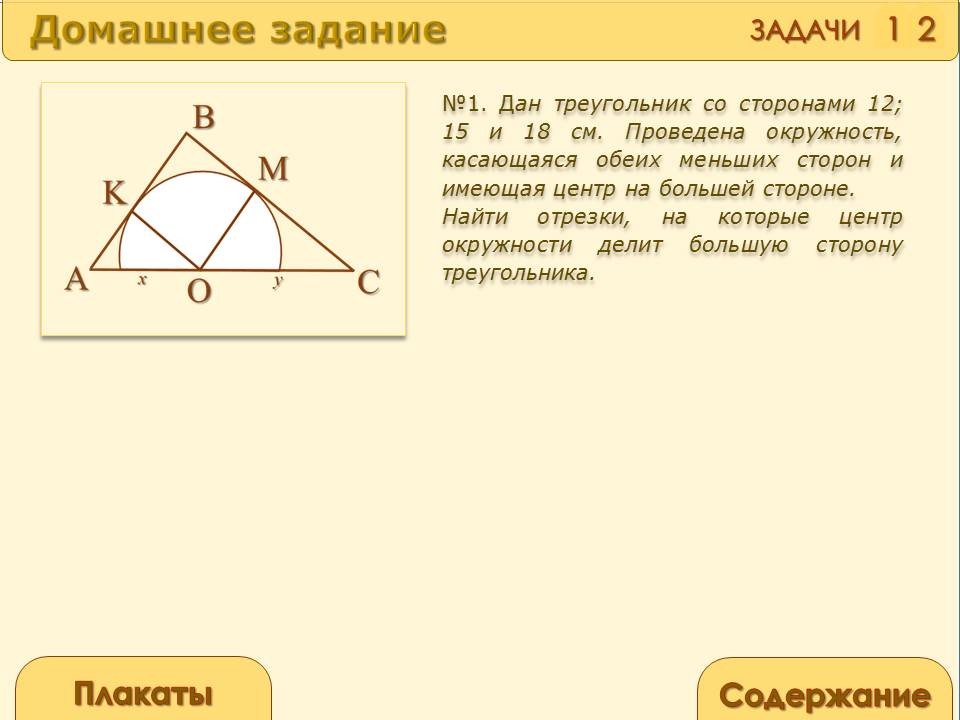
Дан треугольник со сторонами 12; 15 и 18 см. Проведена окружность, касающаяся обеих меньших сторон и имеющая центр на большей стороне. Найти отрезки, на которые центр окружности делит большую сторону треугольника.
Решение:
Пусть ![]() A=
A=![]() ;
; ![]() C=a.
C=a.
AB=12см; BC=15см; AC=18см; AO=x см; OC=y см;
По теореме косинусов имеем:
AB2=BC2+AC2-2BC*AC*cosa
122=152+AC2-2*15*18*cosа
cosa= ![]() =
=![]() =0,75
=0,75
sin![]() =
=![]() sin
sin![]() =
=![]()
![]()
![]() ; cos
; cos![]() =
=![]() =
=![]()
sin![]()
sin![]() =
=![]() =
=![]() ;
;
![]() :
:![]() =
=![]() 5х=72-4х;
9х=72; х=8;
5х=72-4х;
9х=72; х=8;
АО= 8 см.
у=18-х; у=10; ОС=10 см.
Ответ: 8 см и 10 см.
Задача 2 (см.слайды 38-39)
Площадь равностороннего треугольника,
вписанного в окружность, равна Q2. Доказать,
что радиус окружности равен ![]() .
.
Решение:
S(ABC)=Q2 по условию
AB=BC=AC. Пусть BO=OC=AO=R, тогда 3 S(![]() AOC)= Q2;
AOC)= Q2;
3 *R2 *![]() sin120°= Q2 (
sin120°= Q2 (![]() AOC=120°).
AOC=120°).
![]() =
=![]()
R=![]() =
= ![]() .
.
Что и требовалось доказать.