Цели и задачи:
- формирование умения находить площади фигур с опорой на знание площади прямоугольника;
- развитие образного мышления, внимания, смекалки;
- отработка навыка построения геометрического чертежа, измерения сторон и углов, вычисление площади фигур в динамической геометрической среде GeoGebra;
- обучение проведения математического исследования с применением компьютерных технологий;
- расширение математического кругозора, развитие интереса к предмету.
Оборудование:
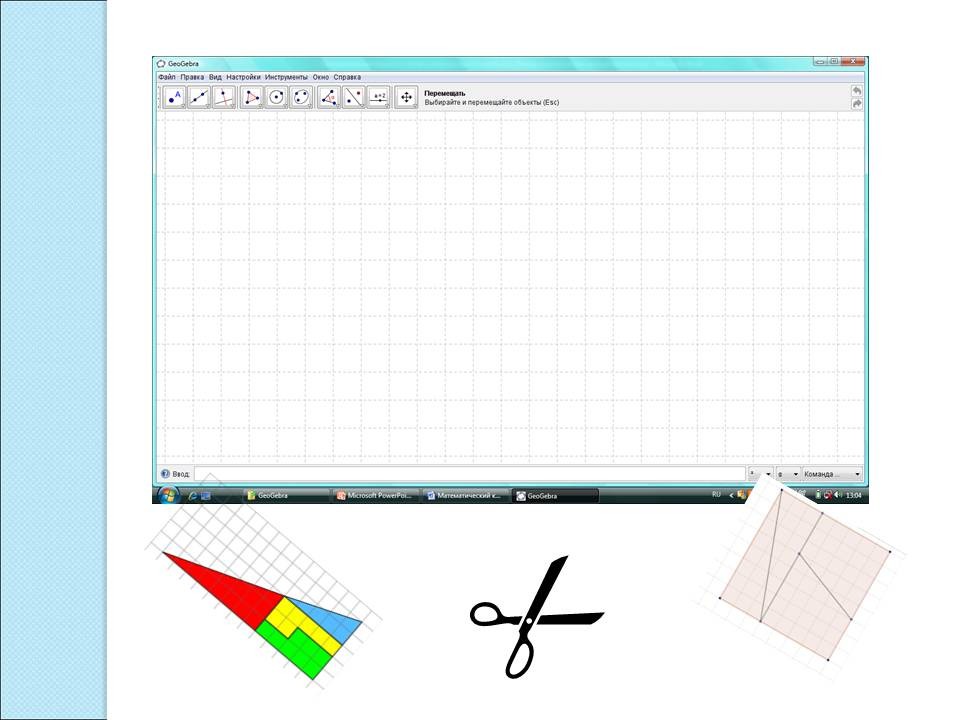
- Планшеты для работы с геометрическими фигурами; разрезные модели геометрических фигур; ножницы; презентация; технологические карты; мобильный компьютерный класс (10 ноутбуков); проектор; экран.
План-конспект
I. Оргмомент (Познакомить с материалами и оборудованием, которые будут использоваться на занятии)
– Здравствуйте, ребята и уважаемые гости! Сегодня занятие математического кружка проведем в гостях у компьютерного клуба. Мы с вами будем находить площади сложных фигур, используя знакомые методы и формулы площадей. Площади, каких фигур мы умеем вычислять? (Прямоугольник, квадрат)
Познакомьтесь с оборудованием, которое понадобится нам на занятии: ...
– Перейдем к решению задач.
II. Разминка.
– На первом листе считайте и записывайте ответы.
Учащимся предлагается решить несколько задач на вычисление площади фигур по готовым чертежам. (Презентация, чертежи дублируются в технологических картах)
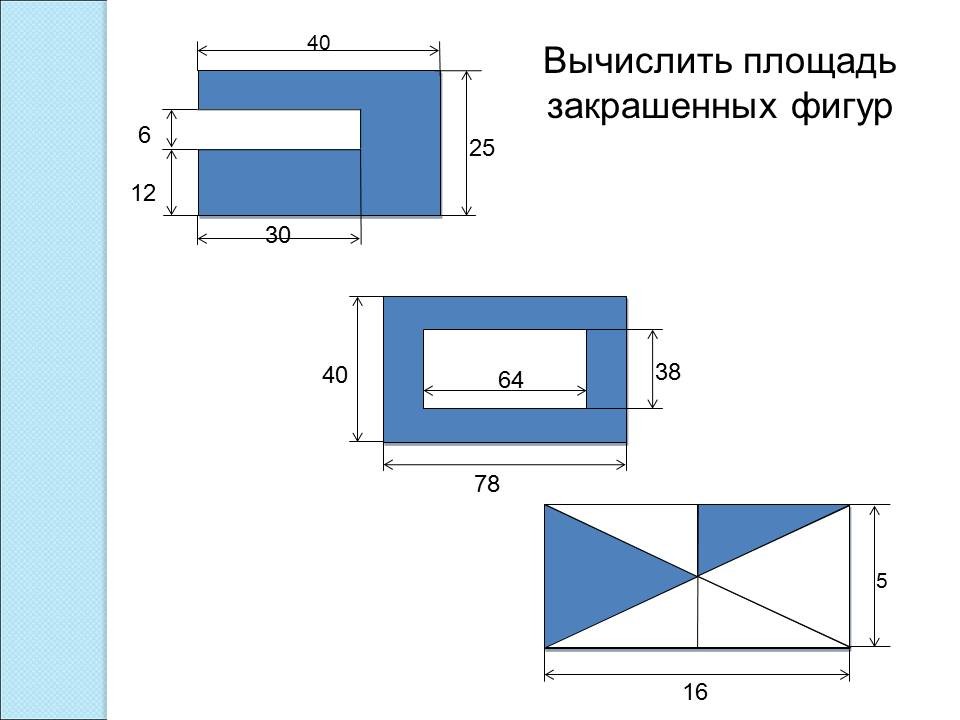
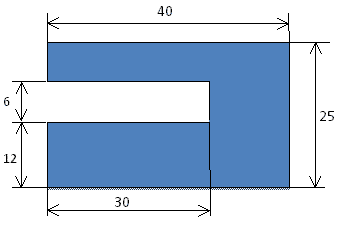
1) Вычислить площадь закрашенной фигуры. Нет ли здесь лишних данных? (Выясняем способ решения задачи, устно проговариваем способ решения)
(25*40-6*30=820)
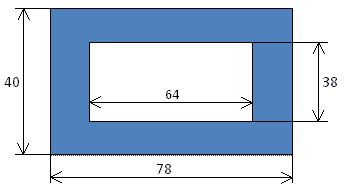
2)
(40*78-64*38=688)
3) Какова площадь заштрихованной площади?
(80 :8*3=30)
4)
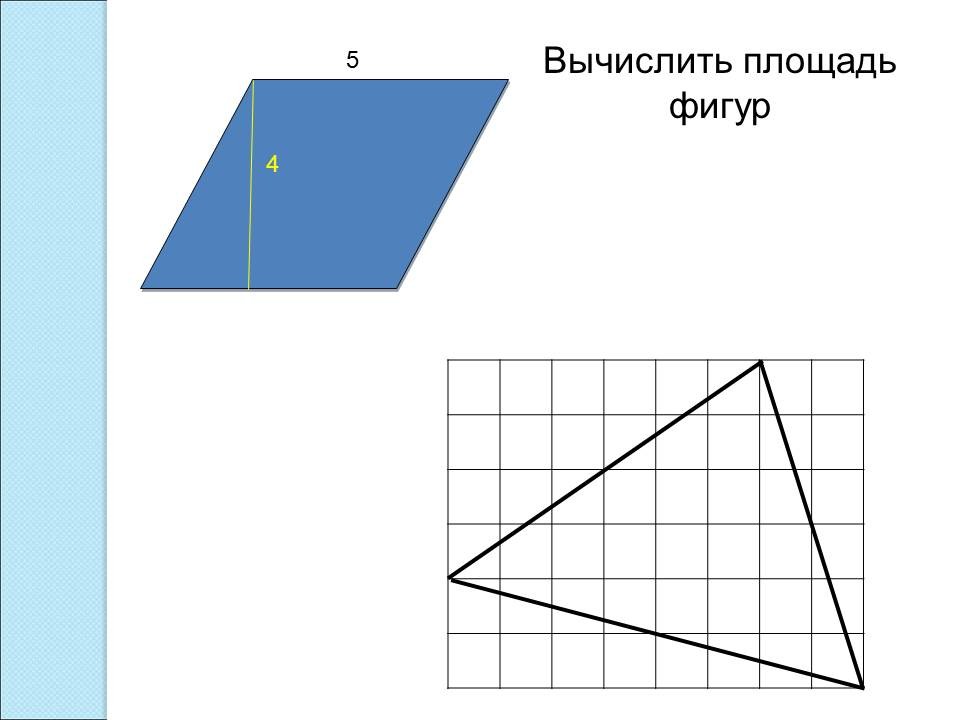
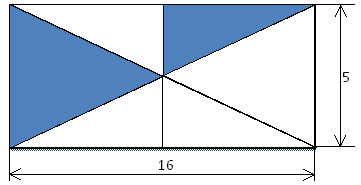
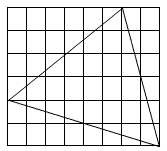
5) Найдите площадь треугольника, если площадь каждой клетки 1 см2.
- Каким свойством площадей мы пользовались? (S=S1+S2+ ... +Sn). Но о чем надо помнить, используя это свойство? (Свойство “работает” только, если части не накладываются друг на друга и не остается “пустоты” внутри новой фигуры)
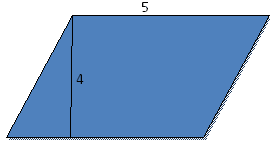
- Какой способ мы использовали при нахождении площади параллелограмма? (Разрезать фигуру и составить фигуру, которую мы знаем)
- Это удобный способ разрезать и переставлять фигуры? (Да)
- Как вы думаете, для чего же люди искали формулы для нахождения площадей фигур? Пусть бы пользовались этим методом.
- Мы предлагаем вам сегодня рассмотреть две геометрические задачи – загадки, которые помогут ответить на этот вопрос.
III. Задача о треугольнике
На слайде анимационная картинка, на которой демонстрируется способ перекладывания фигур.
– Выполняем задание II из технологической карты.
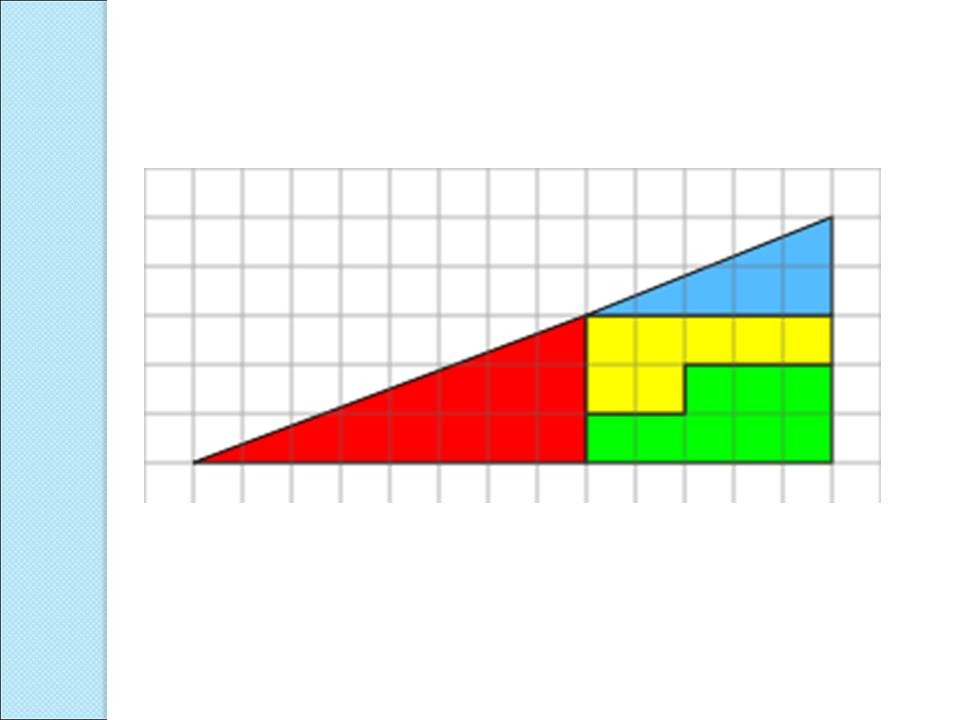
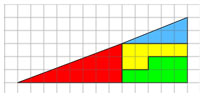
- Возьмите треугольник. Вырежьте его и пользуясь планшетом, найдите длину его катетов. (Что такое катеты?) Запишите измерения на рис. 1 технологической карты.
- Разрежьте треугольник на четыре части по линиям разреза и составьте новый треугольник на планшете, как показано на рис. 2.
- Найдите длину катетов нового треугольника и запишите измерения на рис. 2 технологической карты.
- Что вы заметили? (Катеты равны, но появилась лишняя клетка)
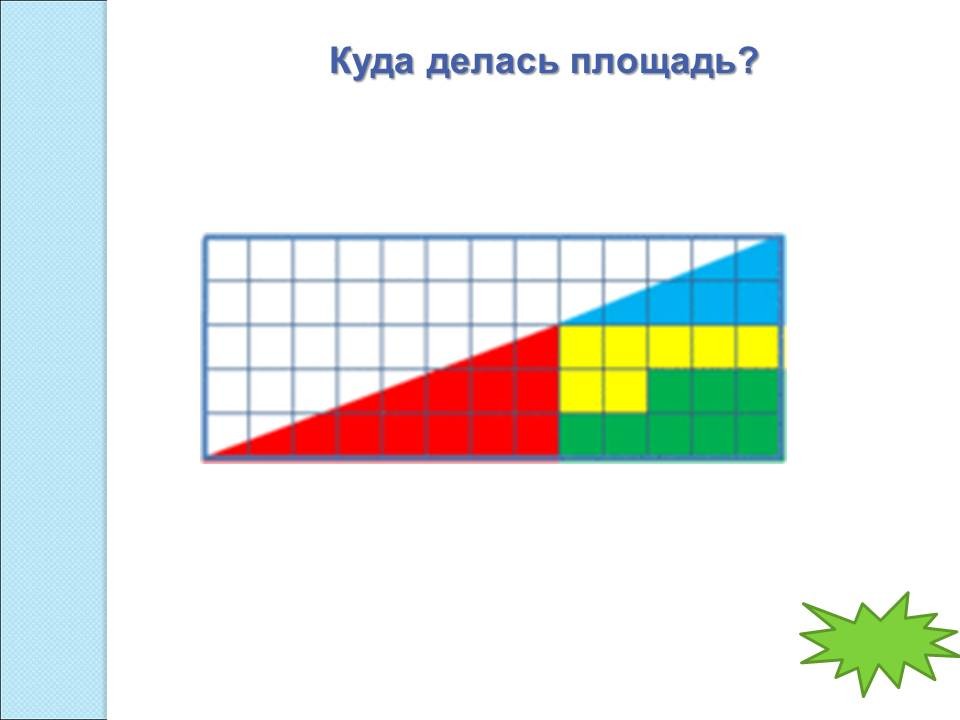
- Куда пропала часть площади? Какие части виноваты? (Рассмотреть фигуры из клеток и треугольники)
| Ребята мы с вами живем в мире
компьютерных технологий, давайте воспользуемся
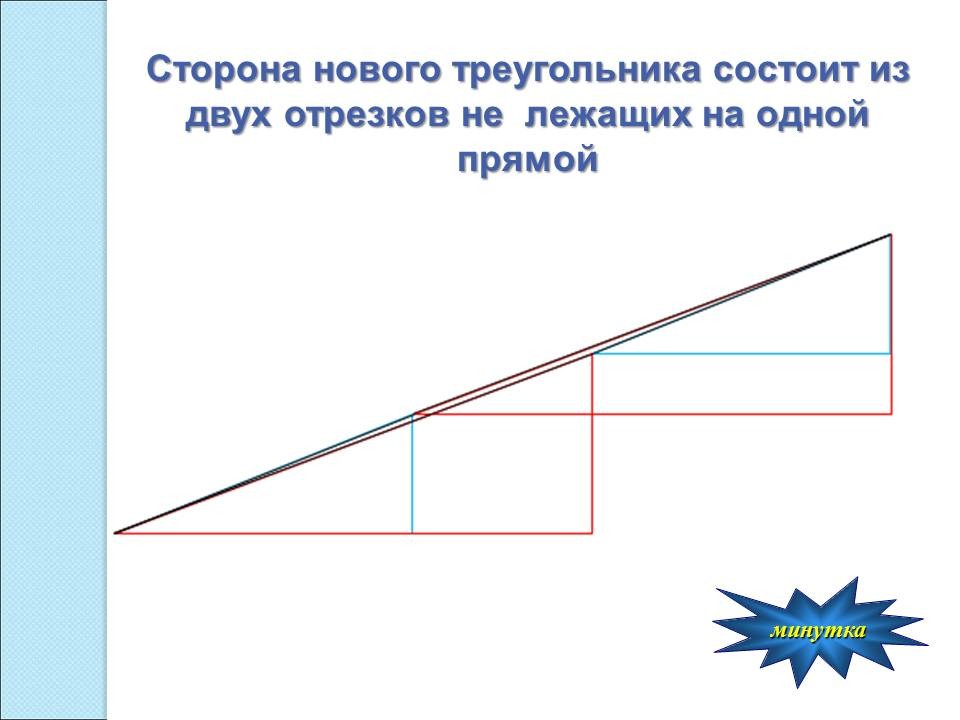
компьютером, средой GeoGebra. Начертите фигуры, из которых состоит треугольник. Видно куда делась площадь? (...) Измерьте углы в маленьких треугольниках. Какой вывод можно сделать? (Гипотенуза нового треугольника не является отрезком прямой) |
|
 |
После этого в презентации
демонстрируется решение задачи. Давайте еще раз убедимся, что площадь фигур в первом треугольнике равна площади всего треугольника на рис. 1 Перейдем ко второй задаче. |
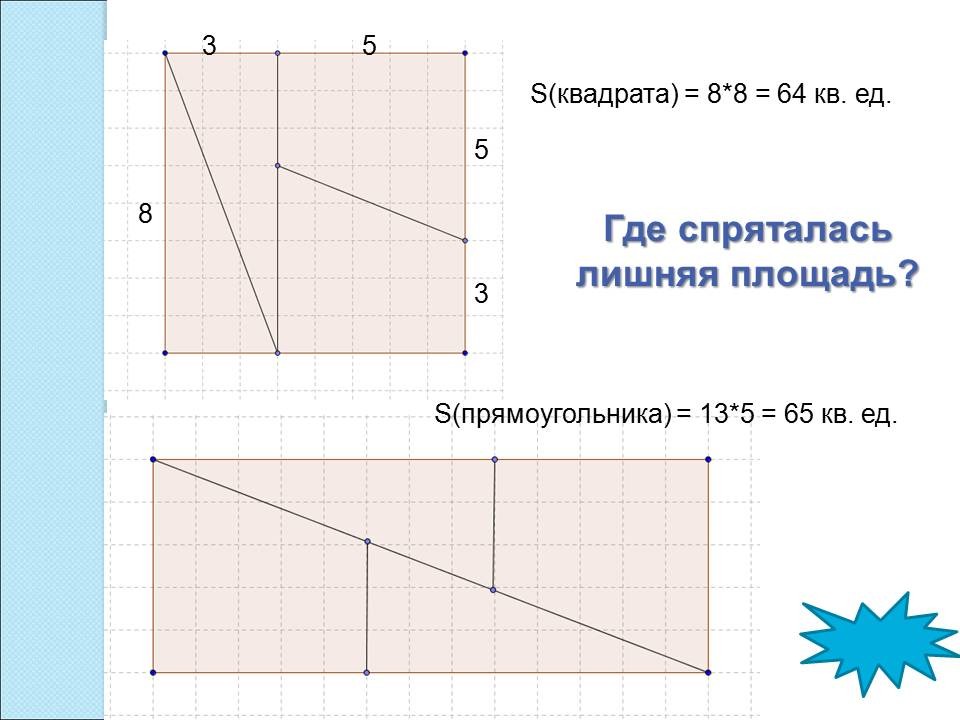
IV. Задача о прямоугольнике.
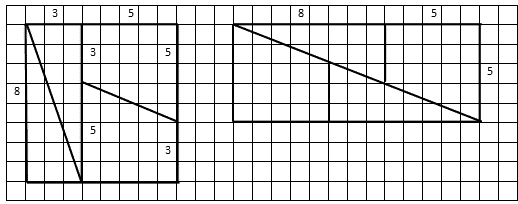
Возьмите технологическую карту. Выполните исследование о том, откуда появилась лишняя площадь.
Выдержка из технологической карты
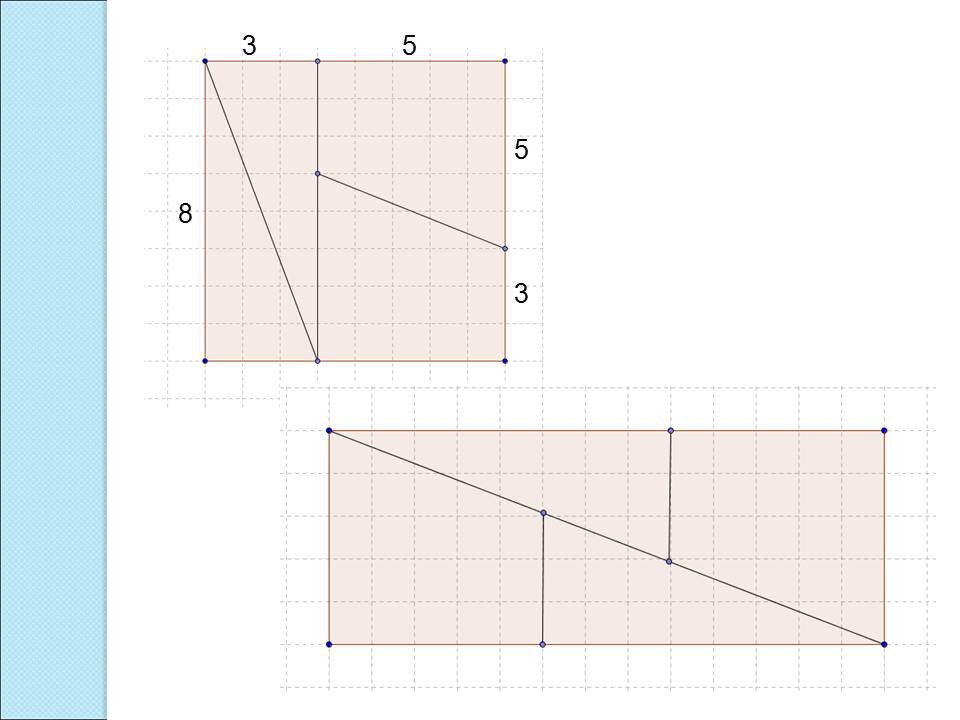
- Возьмите квадрат из раздаточного материала и посчитайте его площадь. ________кв.ед.
- Вырежьте квадрат, разрежьте его на части и составьте на планшетах с клетками прямоугольник, как показано на рисунке (при составлении прямоугольника фигуры можно переворачивать). Какая площадь у новой фигуры? _____________
- Постройте в геометрической среде GeoGebra фигуры, из которых состоит квадрат (Чертите, фигуры так, как они расположены в новой фигуре). Составьте из них требуемый прямоугольник.
- Внимательно рассмотрите полученный чертеж. Что
вы заметили?
___________________________________________________________
V. Подведение итогов.
- Почему мы не увидели ошибок на ручных чертежах, ни на разрезных моделях? Дело в том, что любых измерениях возникают погрешности. Кроме того и при вырезании фигур у нас тоже возникают неточности. Так может быть способ разрезания и перестановке частей вообще не применим? Конечно, его можно применять. Он удобный, наглядный и много раз нас выручал.
- Только в более сложных или сомнительных случаях нужно быть очень внимательным, по возможности применять компьютерные модели.
- Лучше всего изучать геометрию, чтобы научиться вычислять площади любых фигур по формулам.