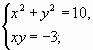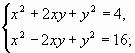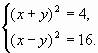Цели урока:
- способствовать формированию навыков исследовательской деятельности обучающихся;
- развивать потребность в нахождении рациональных приемов и способов создания модели и решения математической задачи;
- воспитывать познавательную активность на всех этапах урока
Оборудование: интерактивная доска, проектор, на столах табличка – руководство к действию:
Не ограничивайте полёт своей фантазии, и нестандартные решения всегда найдутся.
А.Н. Колмогоров
Ход урока
I. Актуализация знаний
Добрый день, друзья.
Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их.
Д. Пойа
Перед тем, как входить в воду, т.е. перед решением задачи проведем математическую разминку.
- Что значит решить систему с двумя переменными?
- Способы решения систем уравнений, известные вам к сегодняшнему уроку.
- Алгоритм решения системы уравнений с двумя переменными, одно из которых уравнение второй степени, а другое линейное.
- Что представляет собой график уравнения x2+y2=r2
- Что представляет собой графическое решение уравнения xy=a?
- Сколько решений может иметь система двух уравнений второй степени с двумя переменными?
А теперь можете смело входить в воду
Задания по группам
I группа На индивидуальных системах координат покажите решение уравнения x2+y2=10
II группа На индивидуальных системах координат (прозрачных) покажите решение уравнения xy=-3
III группа Сколько решений имеет система уравнений групп I и II? Покажите это наложением систем координат.
А теперь покажите решение этой системы уравнений аналитически
Решение: 1) xy=-3; отсюда ![]()
Кратко объясните это решение. К какому уравнению вы пришли в ходе решения уравнения?
Вопросы группам
I. В чем преимущества аналитического способа решения?
Преимущество заключается в следующем: получены точные решения системы
II. Есть ли недостатки этого способа? Если есть, то укажите их.
К сожалению, недостатки есть: решение занимает больший промежуток времени, чем хотелось бы.
Итак, какие выводы о решении заданной системы уравнений можно сделать на первом этапе урока
Обучающиеся делают выводы
На этом этапе урока нашу работу можно подтвердить следующими словами Н.Е.Жуковского: «В математике есть своя красота, как в живописи и поэзии»
II. «Погружение» в глубину знаний
Итак, на предыдущем этапе урока мы успешно проплыли часть пути, встретились с загадками и проблемами водного мира. А теперь переходим к следующему этапу урока – «погружению» в глубину знаний.
Перед дорогой по доброй русской традиции повернитесь лицом друг к другу и улыбнитесь. На интерактивной доске появляется высказывание
Три пути ведут к знанию:
- путь размышления – это путь самый благородный;
- путь подражания – это путь самый легкий;
- путь опыта – это путь самый горький.
Конфуций, древний мыслитель и философ Китая
Работая в группах, выберете свой путь и «откройте» для себя новые способы решения этой системы уравнений и учитесь их применять.
В каждой группе на столе находится высказывание современного выдающегося ученого А.Н. Колмогорова: «Не ограничивайте полёт своей фантазии, и нестандартные решения обязательно найдутся».
Вспомните нестандартные методы решения уравнений, которые использовались на уроках, на занятиях элективного курса. Как только у вас возникают идеи, сразу предлагайте их для обсуждения.
I группе предлагаю применить графический способ решения, остальным группам выбор не ограничиваю.
I группа предлагает графический способ решения (показывает на интерактивной доске), на местах в этой группе находят решение с помощью планшетного компьютера.
II группа
Мы предлагаем следующую модель решения (краткая запись с комментариями)
Умножим второе уравнение системы на 2 и сложим затем с первым, получим систему, равносильную заданной:
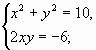
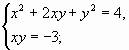
(1)
последняя распадается на две более простые системы:
(2)
(3)
Каждое решение системы (1) является решением хотя бы одной из систем (2) или (3) и наоборот, каждое решение систем (2) и (3) является решением системы (1). Системы (2) и (3) является симметричными.
Реализовать созданную модель предлагаем III группе
III группа
Мы начали решать так же, но далее пошли другим путем. Мы умножили второе уравнение на -2 и вновь сложили с первым уравнением. Получили
Рассматривая каждое уравнение первой строки совместно с каждым уравнение второй строки, приходим к четырем системам линейных уравнений:
Решая устно способом подстановки каждую систему, приходим к тому же множеству решений. Созданную нами модель предлагаем завершить II группе.
I группа
Тогда в принципе и первоначальную систему уравнений можно решить методом подбора?
Да, это тоже один из способов решения системы.
Вопрос I группе:
В каком случае это достигается легко и быстро? (В случае удобных коэффициентов)
III. Подведение итогов этапа урока
Итак, на этом этапе урока мы рассмотрели 3 различные модели решения системы уравнений второй степени с двумя переменными.
Подведем итоги нашей творческой деятельности
Представители групп оценивают свою деятельность
I группа
Мы с полной уверенностью можем сказать, что «открытые» нами нестандартные способы решения систем уравнений запомнятся нам для предстоящей итоговой аттестации, потому что мы работали с одной задачей в разных ситуациях.
2) Я выражаю мнение группы: нам больше всего понравился графический способ решения, потому что он самый короткий и самый красивый
II группа
Мы не совсем согласны с вами. Все подходы к решению поставленной задачи хороши. Везде мы получали изящные, красивые решения.
III группа
Пусть наша группа в своем решении пошла не совсем коротким путем, но зато наш путь был оригинальным, с изюминкой.
III группа
Нам известно, что в контрольно-измерительных материалах к подготовке к экзамену во второй части имеются системы уравнений и задачи, которые решаются с помощью уравнений или систем уравнений.
Учитель
Подумайте и предложите названия своих способов решения системы уравнений, которую мы решаем на сегодняшнем уроке.
На этом этапе урока вы продолжали учиться создавать модели решения задач
Очень приятно, что во всех нестандартных ситуациях на этом этапе урока мы с вами в ходе сотрудничества ощущали радость познания математических законов красоты. Никакая другая наука не имеет таких возможностей выбора методов решения задач. Дальнейшее углубление в знания этой темы состоится в старшей школе при изучении различных видов уравнений и их систем. Для того, чтобы уверенно чувствовать себя в мире различных математических задач, уметь их решать, надо решать их много.
IV этап урока
Реализация моделей решения системы уравнений.
Творческое задание
Составьте текстовую задачу, которая будет сведена к решению заданной системы уравнений
Обучающиеся предлагают для обсуждения составленные условия задач
V. Итог урока
VI. Домашнее задание (дифференцированное)
1 группа
Задача: Два студента и два школьника решают 10 задач. Первый студент и два школьника решат их за 7 минут. Второй студент и два школьника решат их за 10 минут. Два студента решат эти задачи за 12 минут. За какое время решат все задачи два школьника и два студента?
Выяснить, можно ли решить задачу двумя способами: а) с помощью уравнения; б) с помощью системы уравнений. Решите задачу возможными способами.
2 группа и 3 группа творческое задание:
Составить систему уравнений второй степени с двумя переменным и применить к ее решению новые способы, которые можно создать дополнительно.
Литература
- Бунимович, Е.А. ГИА-2015. Математика: тренировочные варианты экзаменационных работ для подготовки к основному государственному экзамену в 9 классе. /авт. - сост. Бунимович, Е.А., Кузнецова, Л.В., Рослова, Л.О. и др. – М.: АСТ: Астрель, 2014. – 94 с.
- Грицаенко, Н.П. Ну-ка, реши!: книга для учащихся. – М.: Просвещение, 1998. – 192 с.
- Лоповок, Л.М. Тысяча проблемных задач по математике: книга для учащихся. – М.: Просвещение, 1995. – 239 с.
- Петраков, И.С. Математика для любознательных: книга для учащихся 8-11 кл. – М.: Просвещение, 2000. – 256 с.
- Сергеев, И.Н., Олехник, С.Н., Гашков, С.Б. Примени математику. – М.: Наука. Гл. ред. физ.-мат. лит., 1989. – 240 с.
- Цыпкин, А.Г., Пинский, А.И. Справочник по методам решения задач по математике для средней школы. – 2-е изд., перераб. и доп. – М.: Наука. Гл. ред. физ.-мат. лит., 1989. – 576 с.