Класс: 10
Образовательная технология: технология развития критического мышления.
Цель урока: ознакомление с основными методами измерения информации и формирование умений вычислить количество информации разными методами.
Задачи урока:
Обучающие:
- краткое знакомство с понятием “количество информации” и с известными методами измерения информации,
- формирование понимания понятия “вероятность”, равновероятных и не равновероятных событий,
- формирование умений вычислить количество информации разными методами.
Воспитывающие:
- воспитание познавательной активности учащихся,
- воспитание положительного отношения учащихся к знаниям,
- воспитание коммуникативной культуры учащихся,
- воспитание интереса к применению методов измерения количества информации в жизни и в профессиональной деятельности.
Развивающие:
- развитие исследовательских навыков учащихся,
- развитие критического мышления при решении практических задач в процессе самостоятельной и групповой исследовательской деятельности учащихся.
Тип урока: урок-лекция с элементами практикума.
Продолжительность урока: 90 минут (спаренный урок).
Методы обучения: объяснительно-иллюстративный, исследовательский.
Оборудование и программное обеспечение:
- интерактивная доска,
- персональный компьютер, мультимедийный проектор и экран для демонстрации учебного материала,
- операционная система MS Windows,
- презентация по данной теме.
План урока:
- Организационный момент. (3 мин)
- Создание проблемной ситуации при постановке темы, цели и задач урока.(7 мин)
- Частичное разрешение проблемной ситуации при реализации намеченного плана урока. (18 мин)
- Применение полученных знаний (15 мин)
- Полное разрешение проблемной ситуации. (20 мин)
- Применение полученных знаний (15 мин)
- Обобщение и систематизация изученного материала. (5 мин)
- Формирование домашнего задания постановкой вопросов для самопроверки. (7 мин)
Ход занятия
1. Организационный момент (проверка присутствующих, проверка готовности к работе).
2. Создание проблемной ситуации при постановке темы, цели и задач урока.
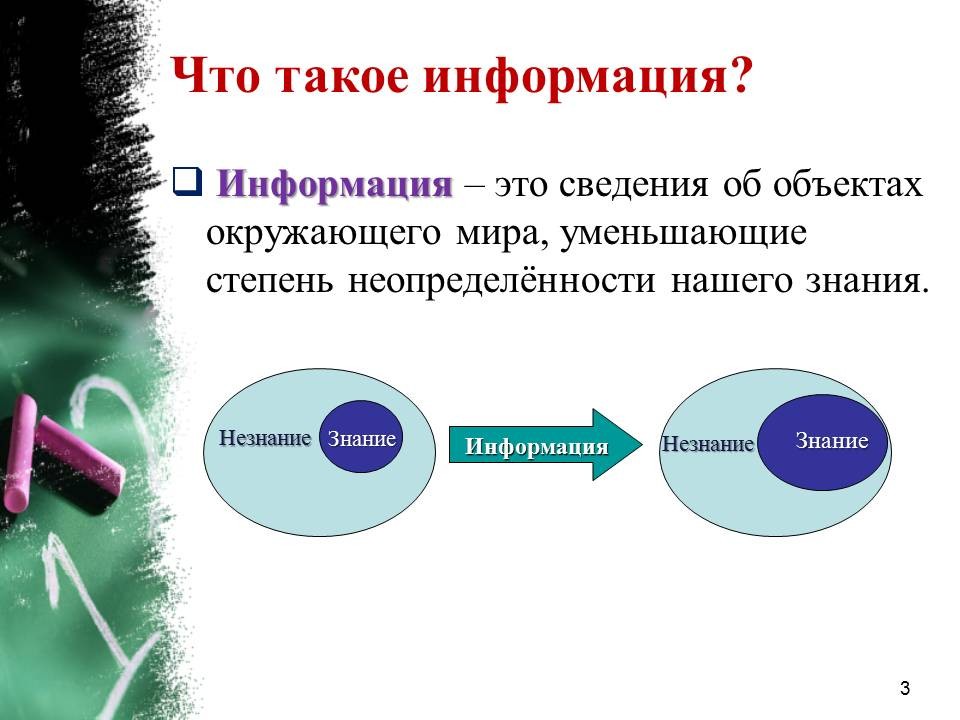
Сегодня мы поговорим о методах измерения количества информации. Понятие информации является одним из фундаментальных понятий современности. Процесс познания окружающего мира приводит к накоплению информации в виде знаний. То есть информация - это знания, которые мы получаем из внешнего мира. Получение новой информации приводит к расширению знаний, т.е., к уменьшению неопределённости нашего знания. Таким образом, мы можем сказать что информация – это сведения об объектах окружающего мира, уменьшающие степень неопределённости нашего знания (см. Рисунок 1).

Рисунок 1
Очень часто нужно определить количество информации в сообщении. Например, вы получили телеграмму: “Встречайте, вагон №5”. Известно, что в составе поезда 16 вагонов. Как узнать, сколько информации вы получили?
3. Частичное разрешение проблемной ситуации при реализации намеченного плана урока.
Проблема измерения количества информации исследуется в теории информации, основанной американским инженером и математиком Клодом Шенноном. Существует два подхода к измерению информации:
- алфавитный подход,
- содержательный (или вероятностный) подход.
Перед тем, как дать подробное описание указанных подходов, дадим основные определения.
- Алфавит – это множество символов, используемых при записи текста.
- Мощность алфавита – это количество символов алфавита.
- Информационный вес одного символа – это количество информации в одном символе.
- Информационный вес символа двоичного алфавита принят за единицу измерения информации и называется 1 бит.
Рассмотрим следующую задачу:
Задача 1: Допустим, что мощность алфавита равна S.Чему равно количество информации в сообщении длины l? Известно, что символы этого сообщения принадлежат данному алфавиту.
Впервые эту задачу попытался решить американский инженер Ричард Хартли в 1928 году. Он предложил меру для измерения количества информации в сообщении с равновероятными символами, т.е., в случае, когда ни один из символов не имеет преимущества перед другими символами. Работы Р.Хартли составляют сущность алфавитного подхода измерения информации.
Согласно идеям Р.Хартли, каждый символ сообщения имеет S возможностей выбора. Следовательно, сообщение длины l имеет S l возможностей выбора. Тогда количество информации в сообщении длины l равно логарифму S l:
![]()
Заметим, что в задаче Р. Хартли
- Каждый символ сообщения содержит log2(S) информации,
- Следовательно, сообщение длины l должно содержать в l раз больше информации, т.е. l * log2(S) информации.
4. Применение полученных знаний.
Решим следующие задачи.
Задача 2: Симметричная монета с двумя сторонами (названными “Орёл” и “Решка”) бросается вверх. Чему равно количество информации в сообщении о том, что стороной вверх выпала “Решка”?
Решение:
N = 2
l = 1
I = ?
I = 1 * log2(2) = 1 бит
Ответ: 1 бит.
Задача 3: Бросается симметричный шестигранный игральный кубик, на гранях которого написаны числа 1 – 6. Вычислить количество информации в сообщении о том, что стороной вверх выпала сторона с числом 1.
Решение:
N = 6
l = 1
I = ?
Ответ: I = log2(6) = 2,585 бит
Задача 4: Сообщение, записанное символами алфавита мощности 32, содержит 80 символов. Чему равно количество информации в сообщении?
Решение:
S = 32
l = 140
I = ?
Ответ: I = 80 * log2(32) = 80* 5 = 400 бит
5. Полное разрешение проблемной ситуации.
В указанных примерах сообщений возможные события были равновероятны. Но существует множество ситуаций, когда возможные события имеют различные вероятности реализации. Например, если в ящике белых шаров больше, чем чёрных, то вероятнее взять белый шар, чем чёрный. Или, когда сообщают прогноз погоды, то сообщение о том, что будет дождь, более вероятно летом, а сообщение о снеге – зимой. Как вычислить количество информации в сообщении с символами, имеющими разные вероятности?
Американский инженер и математик К. Шеннон продолжил работы Р. Хартли и в 1948 году предложил меру для измерения количества информации в сообщении с символами, имеющими различные вероятности реализации. Работы К. Шеннона составляют сущность содержательного (или вероятностного) подхода измерения информации.
Дадим краткую историческую справку. К. Шеннон является основателем теории информации. Он первым предложил использовать термин “бит” для обозначения наименьшей единицы измерения информации. К. Шеннон ввёл следующие понятия (которые мы рассмотрим на уроке):
- понятие собственной информации как количества информации, содержащей в определённом символе сообщения,
- понятие информационной энтропии как меры неопределенности появления символа в сообщении.
Дадим их краткое описание. Сначала дадим классическое определение вероятности.
Вероятность p случайного события равна отношению числа исходов ki, благоприятствующих данному событию, к общему числу равновозможных исходов: pi = ki/S
К. Шеннон ввёл количество информации (в битах) I(pi) i-го символа алфавита следующим образом:
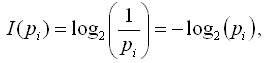
pi где - вероятность появления i-го символа алфавита.
Величину I(pi) называют собственной информацией i-го символа алфавита.
По формуле собственной информации видно, что чем меньше вероятность i-го символа алфавита, тем больше его собственная информация. Следовательно, в задаче 2 (с бросанием симметричной монеты с двумя сторонами) полученная информация I = 1 бит меньше, чем полученная информация I = 2,585 в задаче 3 (с бросанием симметричного шестигранного игрального кубика). Следовательно, чем меньше мы знаем о сообщении, тем больше информации в ней содержится.
В своей основополагающей работе “Математическая теория связи” (1948 год) (см. [1]) К. Шеннон рассмотрел также среднее количество информации в сообщении, которую назвал информационной энтропией.
Информационная энтропия Н определяется следующим образом:
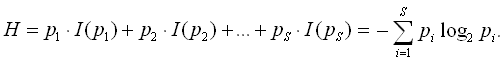
Дадим краткую историческую справку об энтропии. Понятие энтропии впервые было введено немецким физиком Р. Клаузиусом в термодинамике в 1865 году. Австрийский физик Л. Больцман и американский физик У. Гиббс связали энтропию с вероятностью и описали термодинамическую систему с помощью энтропии. К. Шеннон ввёл понятие энтропии в теорию информации.
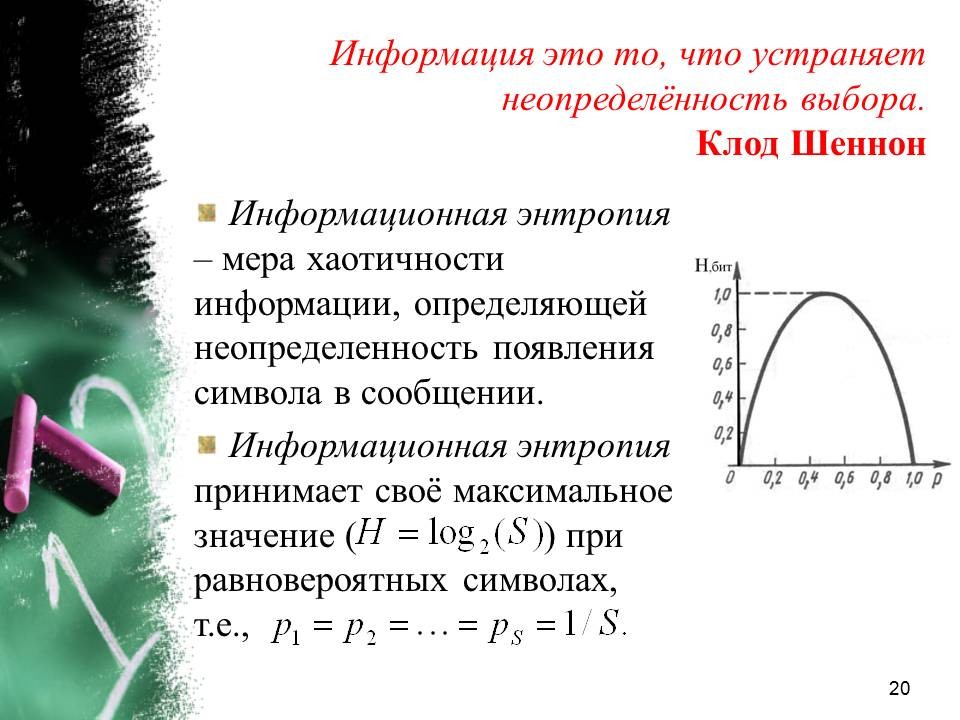
Заметим, что информационная энтропия – это мера хаотичности информации, определяющей неопределенность появления символа в сообщении. График двоичной энтропии (при S = 2) в зависимости от p = pi (тогда согласно свойствам вероятности p2 = 1 - p1) приведён на рисунке:
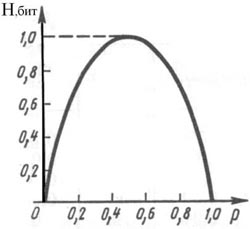
Отметим, что двоичная энтропия ![]() играет большую роль в
теории информации.
играет большую роль в
теории информации.
Заметим, что информационная энтропия принимает
своё максимальное значение (![]() ) при равновероятных символах,
т.е.
) при равновероятных символах,
т.е.
![]()
В случае равновероятных символов формула Шеннона совпадает с формулой Хартли:
![]()
6. Применение полученных знаний.
Решим следующие задачи.
Задача 2: В корзине лежат 8 чёрных и 24 белых шаров. Сколько информации несет сообщение о том, что достали шар фиксированного цвета? Сколько информации несет сообщение о том, что достали шар любого цвета?
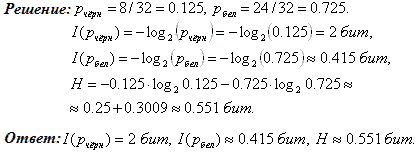
Задача 5: Бросается несимметричная четырёхгранная пирамида. Известно, что
![]()
являются вероятностями выпадения граней пирамиды. Вычислить количество полученной информации о выпадении какой-то грани пирамиды.
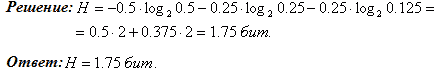
7. Обобщение и систематизация изученного материала.
В ходе урока мы рассмотрели два подхода измерения информации.
- При алфавитном подходе измерения информации предполагается, что все символы алфавита встречаются в сообщениях, записанных с помощью этого алфавита, одинаково часто. Однако в действительности символы алфавитов в сообщениях появляются с разной частотой.
- При вероятностном подходе измерения информации количество информации в сообщении о некотором событии зависит от вероятности этого события. Чем меньше вероятность некоторого события, тем больше информации содержит сообщение об этом событии. Среднее количество информации достигает максимального значения при равновероятных событиях.
8. Формирование домашнего задания постановкой вопросов для самопроверки.
Ну что ж, время урока подходит к концу.
Давайте вспомним, что такое:
- Информация?
- Собственная информация?
- Информационная энтропия?
- Вероятность?
Какие подходы измерения информации вы знаете?
Хорошо!
Пожалуйста, повторите дома записи в тетради. Запишите домашнее задание:
До свидания!
Литература.
- Информатика и ИКТ. Учебник. 10 класс / Под ред. Проф. Н.В. Макаровой. - СПб.: Питер, 2012.
- Работы по теории информации и кибернетике. / Шеннон К. — М.: Изд-во иностранной литературы, 1963.
- https://urok.1sept.ru/articles/572186/