Цель урока: Определить закономерности преобразования графиков функций.
Задачи:
Образовательная:
- Научить обучающихся строить графики функций путем преобразования графика данной функции, применяя параллельный перенос, сжатие (растяжение), различные виды симметрии.
Воспитательная:
- Воспитывать личностные качества обучающихся (умение слушать), доброжелательность по отношению к окружающим, внимательность, аккуратность, дисциплинированность, умение работать в группе.
- Воспитывать интерес к предмету и потребности в приобретении знаний.
Развивающая:
- Развивать пространственное воображение и логическое мышление обучающихся, умение быстро ориентироваться в обстановке; развивать сообразительность, находчивость, тренировать память.
Оборудование:
- Мультимедийная установка: компьютер, проектор.
Литература:
- Башмаков, М. И. Математика [Текст]: учебник для учреждений нач. и сред. проф. образования/ М. И. Башмаков.- 5-е изд., испр. – М.: Издательский центр “Академия”, 2012. – 256 с.
- Башмаков, М. И. Математика. Задачник [Текст]: учеб. пособие для образоват. учреждений нач. и сред. проф. образования/ М. И. Башмаков.– М.: Издательский центр “Академия”, 2012. – 416 с.
План урока:
- Организационный момент (3 мин).
- Актуализация знаний (7 мин).
- Объяснение нового материала (20 мин).
- Закрепление нового материала (10 мин).
- Итог урока (3 мин).
- Домашнее задание (2 мин).
Ход урока
1. Орг. момент (3 мин).
Проверка присутствующих.
Сообщение цели урока.
Основные свойства функций как зависимостей между переменными величинами не должны существенно меняться при изменении способа измерения этих величин, т. е. при изменении масштаба измерения и начала отсчета. Однако за счет более рационального выбора способа измерения переменных величин обычно удается упростить запись зависимости между ними, привести эту запись к некоторому стандартному виду. На геометрическом языке изменение способа измерения величин означает некоторые простые преобразования графиков, к изучению которых мы сегодня и перейдем.
2. Актуализация знаний (7 мин).
Прежде чем будем говорить о преобразованиях графиков, повторим пройденный материал.
Устная работа. (Слайд 2).
Даны функции:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
1. Найти ![]() .
.
2. Найти ![]() .
.
3. Охарактеризуйте графики функций: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
3. Объяснение нового материала (20 мин).
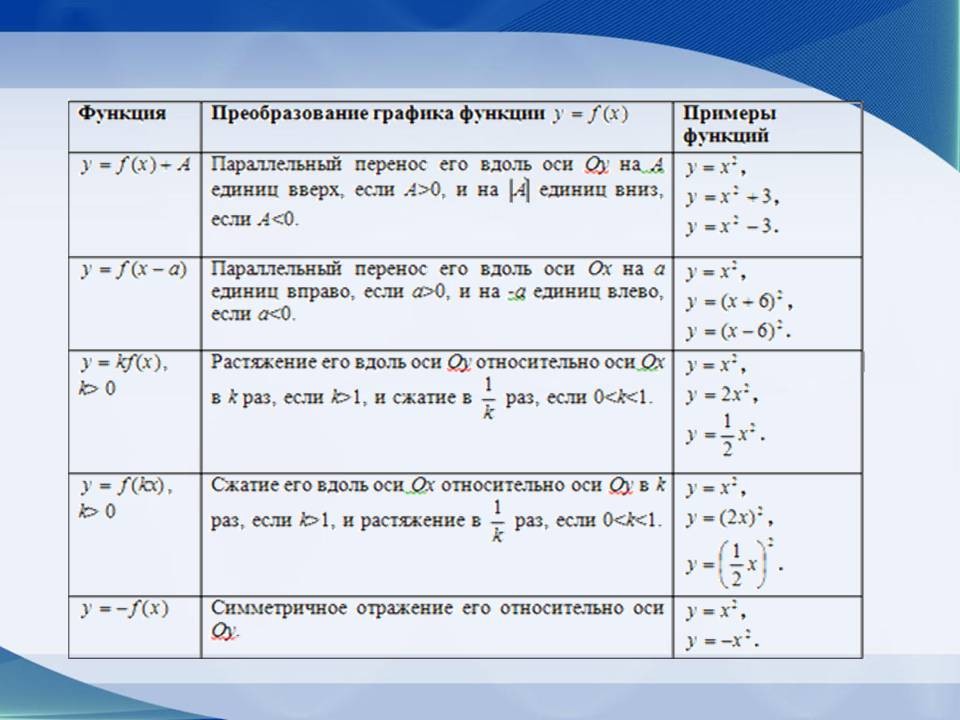
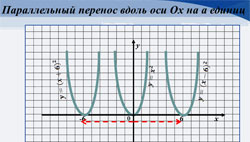
Простейшие преобразования графиков – это их параллельный перенос, сжатие (растяжение) и некоторые виды симметрии. Некоторые преобразования представлены в таблице (Приложение 1), (Слайд 3).
Работа в группах.
Каждая группа строит графики заданных функций и представляет результат для обсуждения.
- 1 группа строит графики функций:
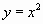 ,
,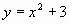 ,
, 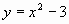 .
. - 2 группа строит графики функций:
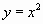 ,
, 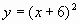 ,
, 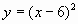 .
. - 3 группа строит графики функций:
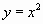 ,
, 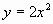 ,
, 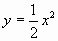 .
. - 4 группа строит графики функций:
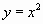 ,
, 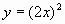 ,
, 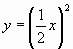 .
. - 5 группа строит графики функций:
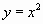 ,
, 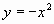 .
.
| Функция | Преобразование графика
функции |
Примеры функций | Слайд |
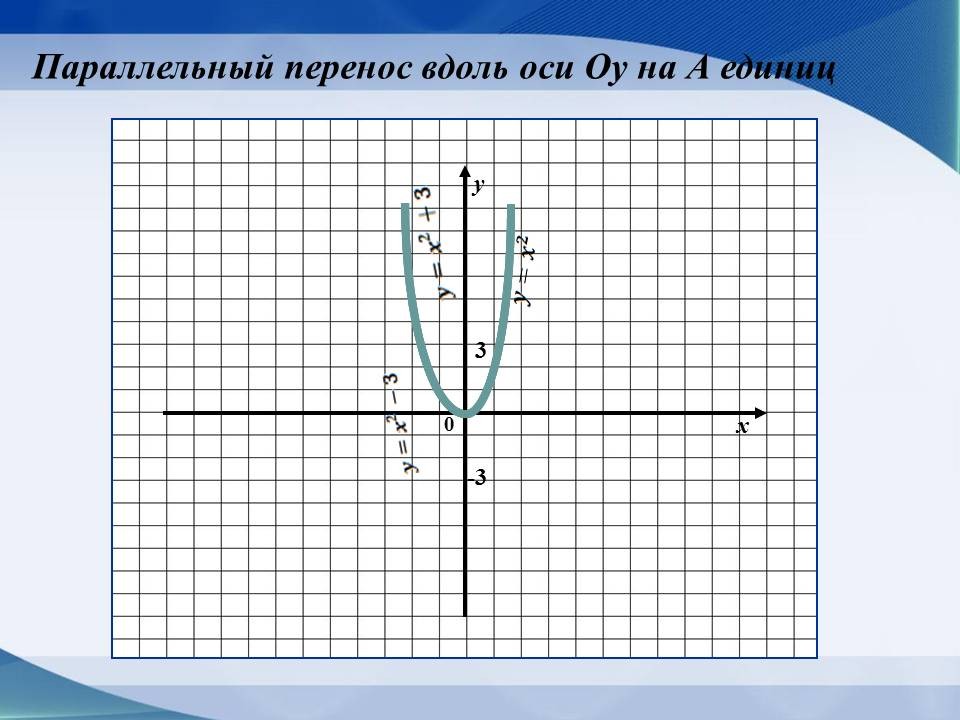
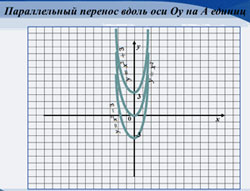
| Параллельный перенос его вдоль оси Оу на А единиц вверх, если A>0, и на |A| единиц вниз, если А<0. |
|
(Слайд 4)
|
|
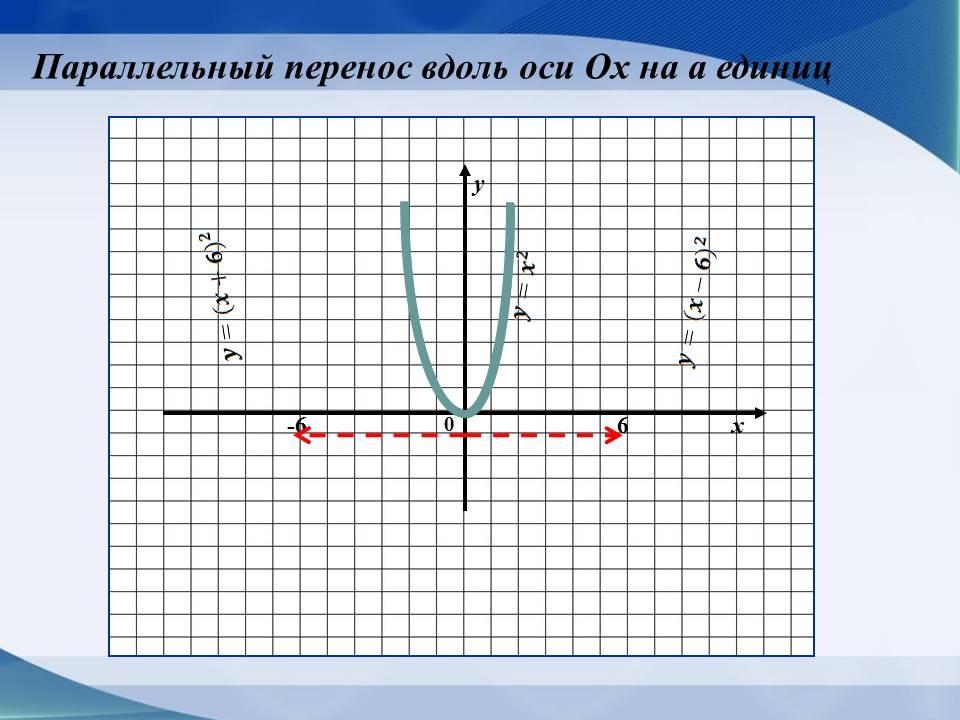
| Параллельный перенос его вдоль оси Ох на а единиц вправо, если а>0, и на -а единиц влево, если а<0. |
|
(Слайд 5)
|
|
k> 0 |
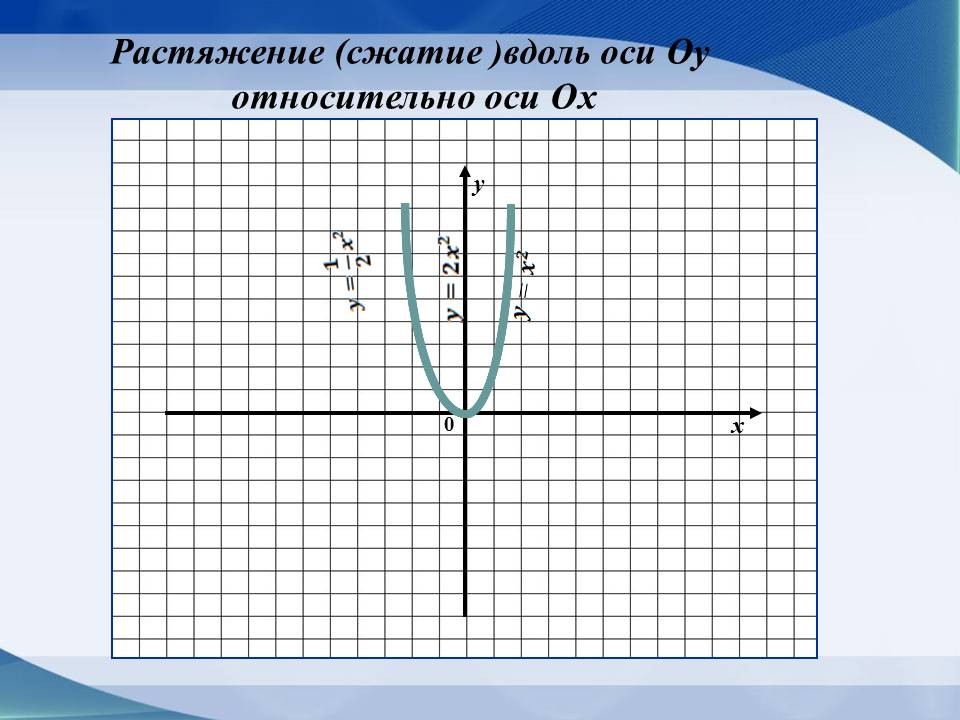
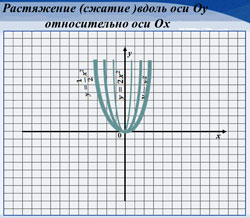
Растяжение его вдоль оси Оу
относительно оси Ох в k раз, если k>1, и
сжатие в |
|
(Слайд 6)
|
k> 0 |
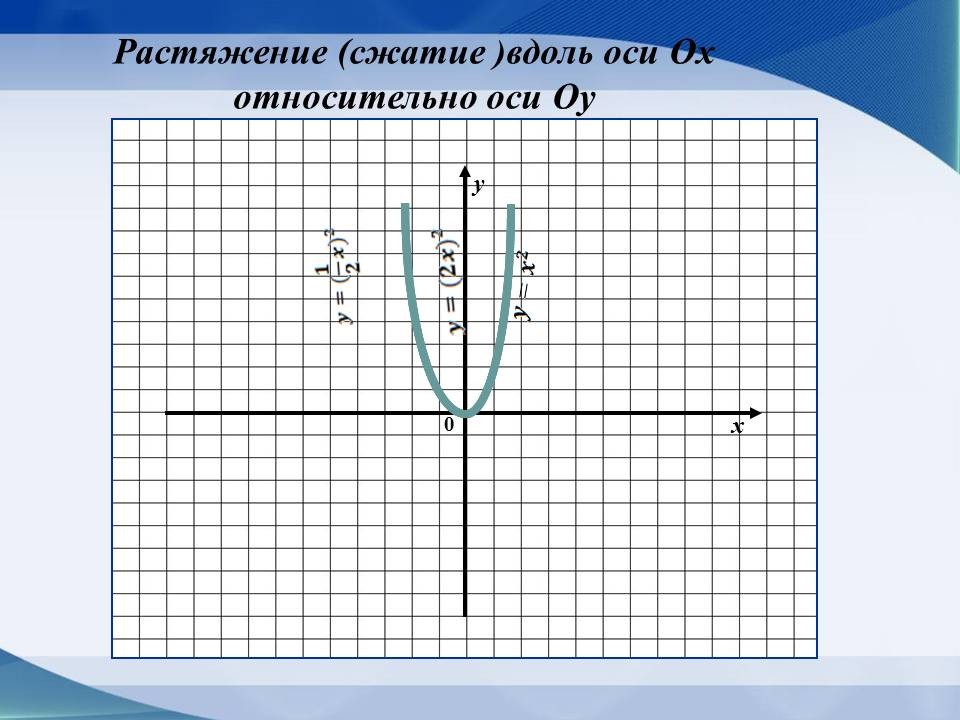
Сжатие его вдоль оси Ох
относительно оси Оу в k раз, если k>1, и
растяжение в |
|
(Слайд 7)
|
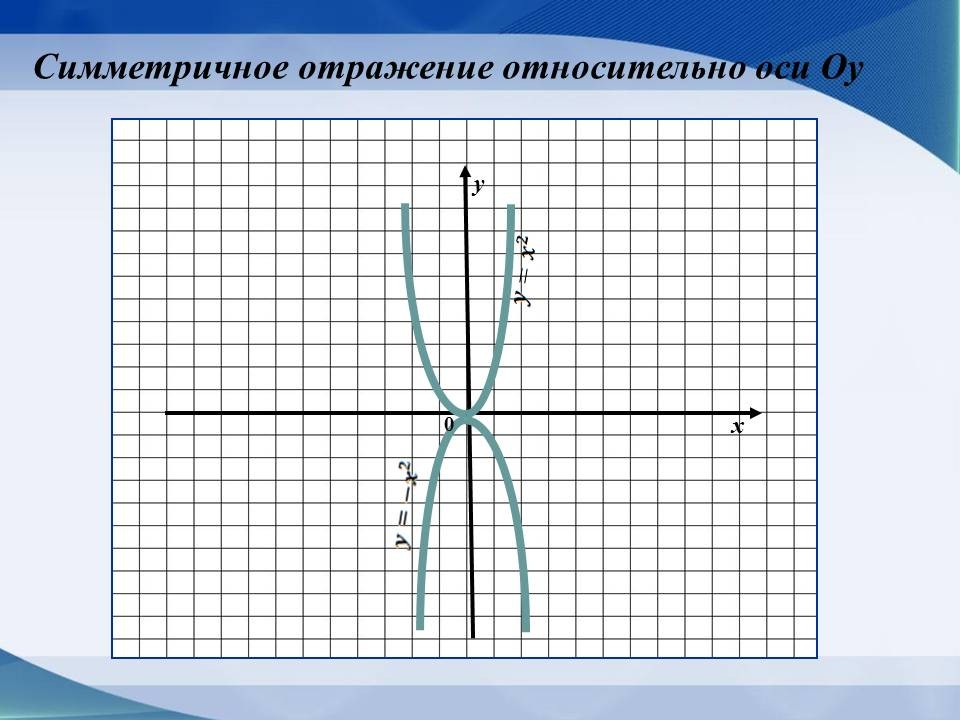
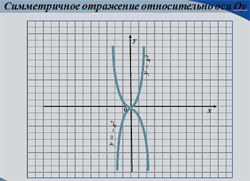
| Симметричное отражение его относительно оси Оу. |
|
(Слайд 8)
|
4. Закрепление нового материала (10 мин).
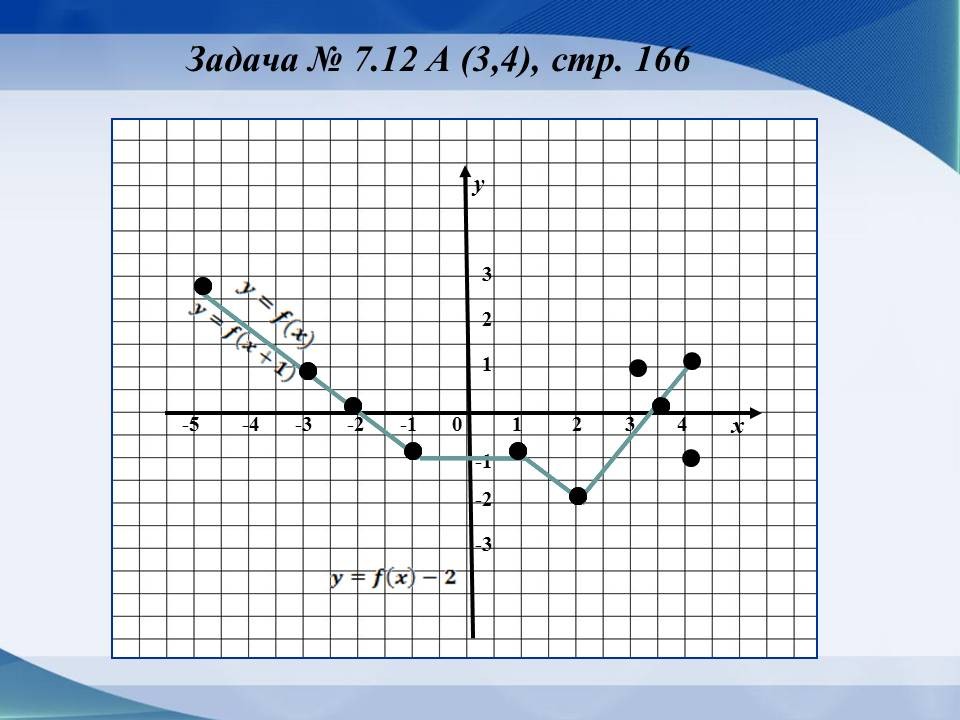
Решение задачи № 7.12 (3,4), стр. 166 (Слайд 9)
5. Итог урока (3 мин).
6. Домашнее задание (2 мин).
Проработка конспектов лекций, учебника стр. 133-136, решить задачу (на выбор по уровню сложности) № 7.12: А (5,6), Б (2,4), В (1,2) (Слайд 10).