“Я слышу – я забываю, я вижу – я запоминаю, я делаю – я усваиваю”. (китайская мудрость)
Цели на урок:
- дидактические: формирование умения строить сечения тетраэдра и параллелепипеда, применять полученные знания для решения задач;
- развивающие: развитие умения формулировать гипотезы; развитие познавательного интереса, логического мышления, интеллектуальных способностей; формирование математической речи;
- воспитательные: воспитание у учащихся таких качеств личности как познавательная активность, самостоятельность, упорство в достижении цели, потребность в приобретении и углублении знаний, вырабатывать умение слушать и вести диалог, формирование эстетических навыков при оформлении записей в тетради.
Тип урока: урок освоения новых знаний
Структура урока:
- Мотивационный этап.
- Цели урока.
- Этап изучения нового материала.
- Этап закрепления нового материала (совместная деятельность учащихся)
- Самостоятельная работа (индивидуальная работа учащихся)
- Рефлексия.
- Этап информации учащихся о домашнем задании.
Оборудование: компьютер, мультимедийный проектор, экран, презентация “Задачи на построение сечений”, доска, мел, раздаточный материал с домашним заданием, индивидуальные карточки для рефлексии.
Замечание: данный урок проводится после изучения тем “Параллельность прямых и плоскостей” и “Перпендикулярность прямых и плоскостей”.
ХОД УРОКА
1. Мотивационный этап.
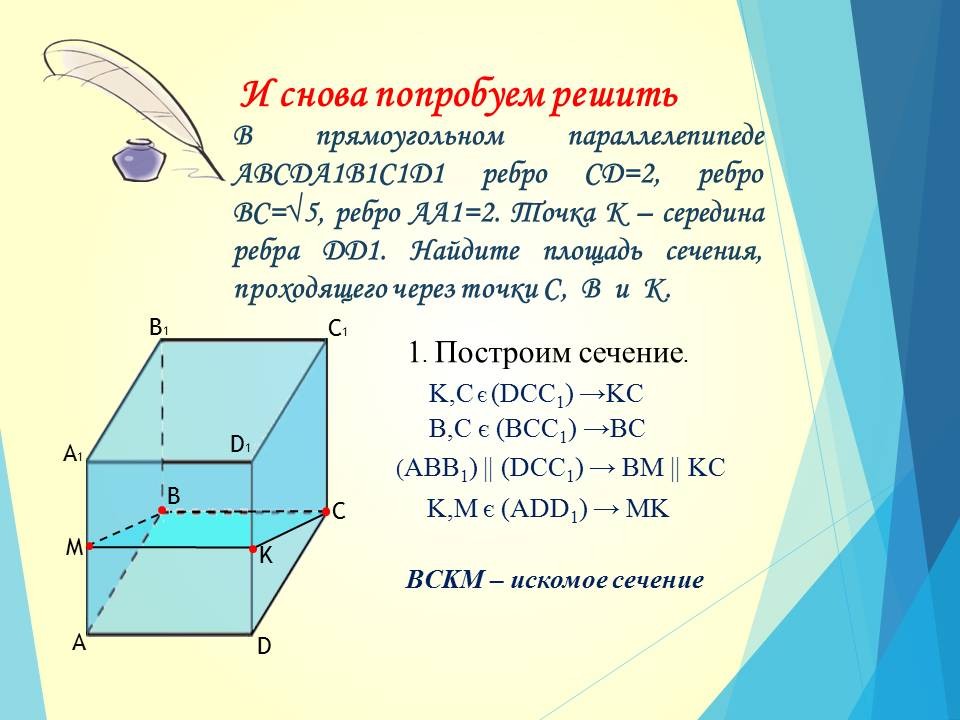
Для начала попробуем решить задачу.

- Каких знаний вам не хватает чтобы решить поставленную задачу?
- Какова, на ваш взгляд, тема над которой мы будем работать на уроке?

- Какие цели на урок вы можете перед собой поставить?

2. Этап изучения нового материала.
Для решения многих геометрических задач, полезно строить на рисунке их сечения различными плоскостями. Сегодня на уроке мы разберем основные приемы построения сечений тетраэдра и параллелепипеда. Уточним, сначала, что понимается под сечением.


- Как вы думаете, какие фигуры могут оказаться сечением тетраэдра? Параллелепипеда? От чего это зависит?

Прежде, чем приступить к построению сечений тетраэдра и параллелепипеда, следует иметь в виду
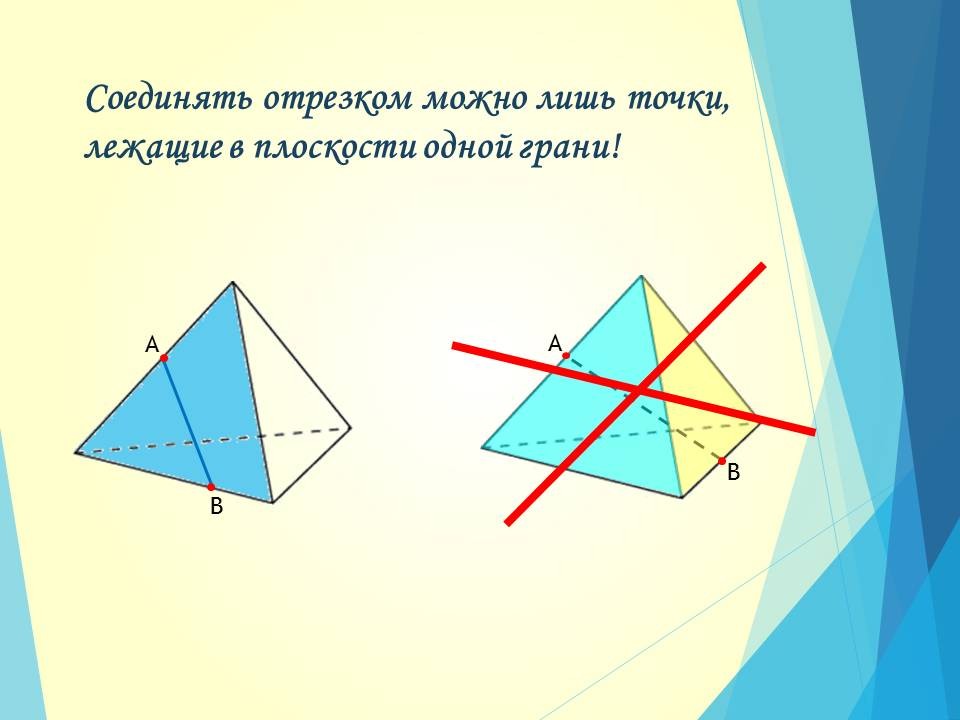
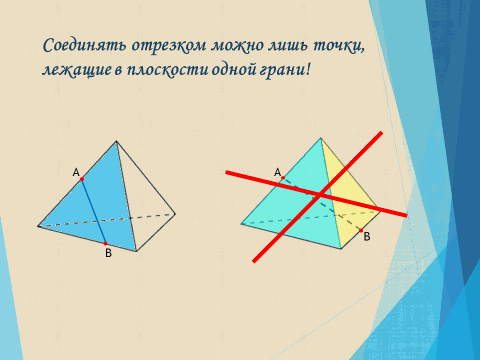
1) Соединять отрезком можно лишь точки, лежащие в плоскости одной грани.
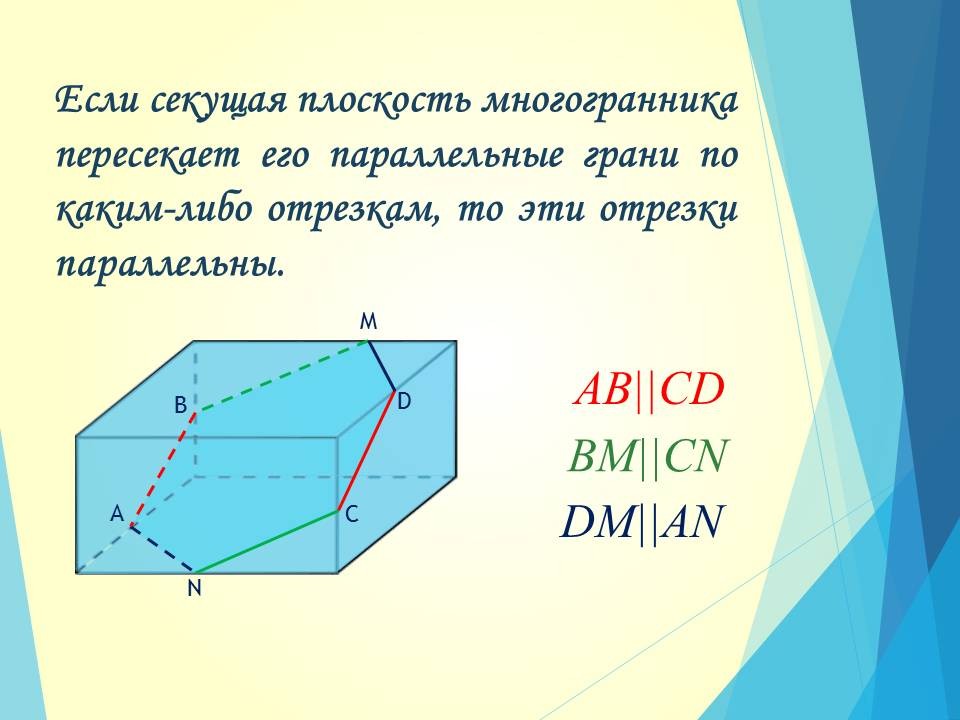
2) Если секущая плоскость многогранника пересекает его параллельные грани по каким-либо отрезкам, то эти отрезки параллельны.
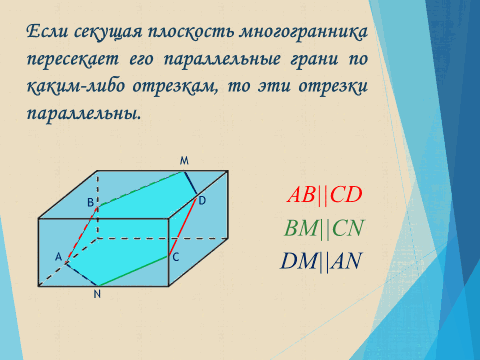
- Как вы думаете, почему?
- Сформулируйте свойство параллельных плоскостей.
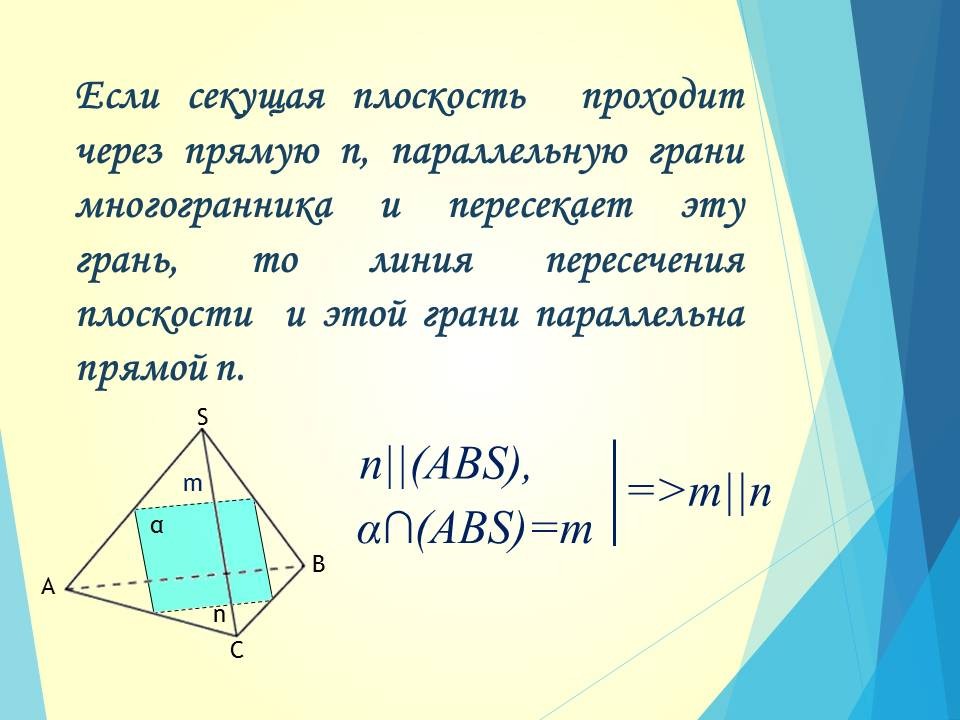
3) Если секущая плоскость a проходит через прямую n, параллельную грани многогранника и пересекает эту грань, то линия пересечения плоскости a и этой грани параллельна прямой n.
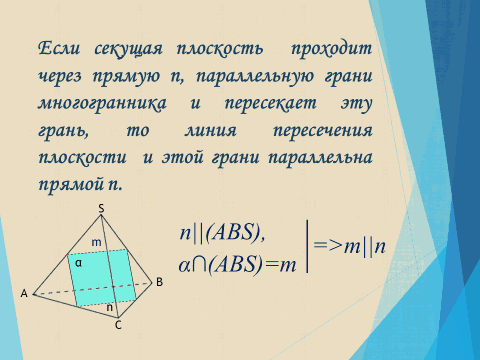
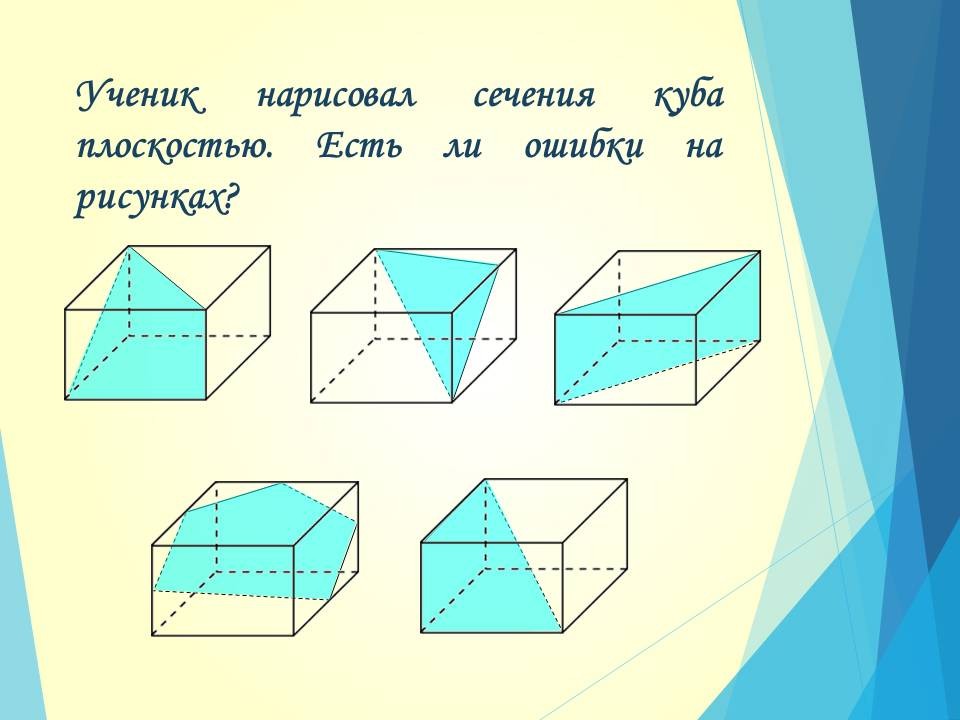
Попробуем осознать то, что записали, отыскав ошибки в построении сечений.
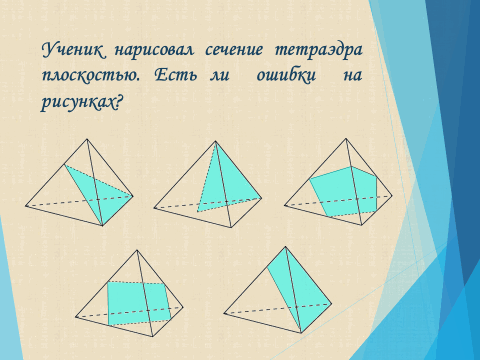
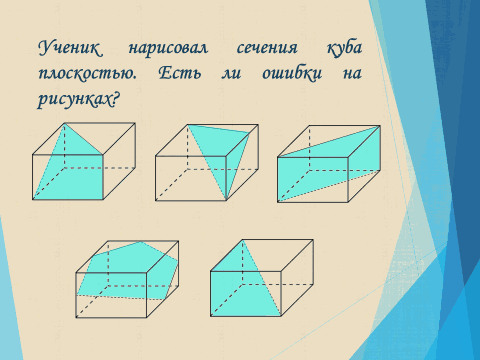
3. Этап закрепления нового материала.
Итак, теоретическая часть урока подошла к концу, мы “увидели и запомнили”, а теперь начинаем “делать и усваивать”.
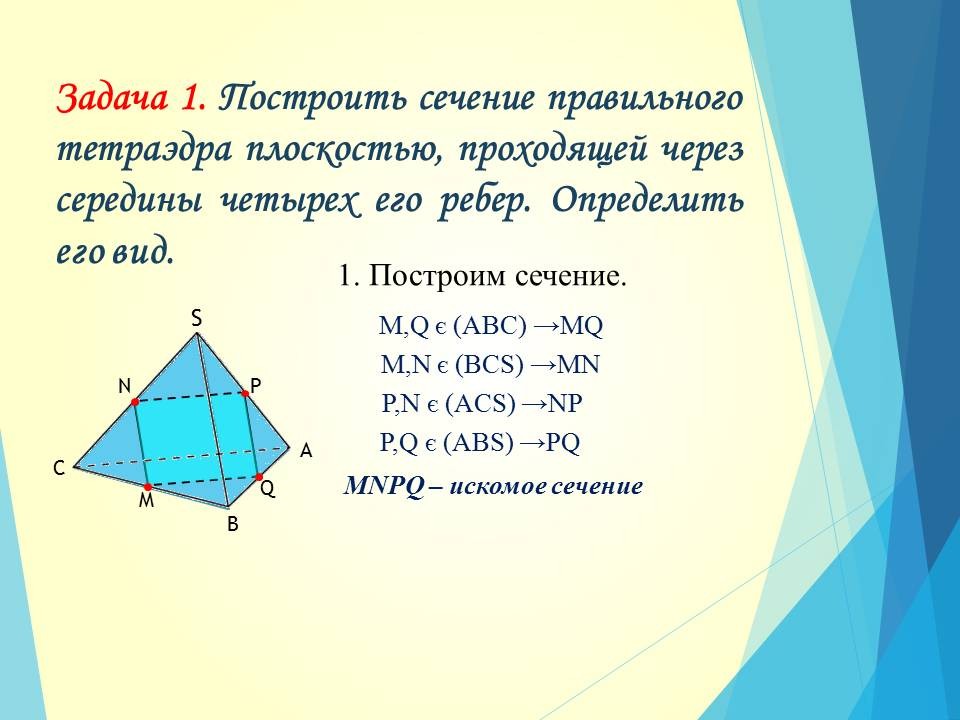
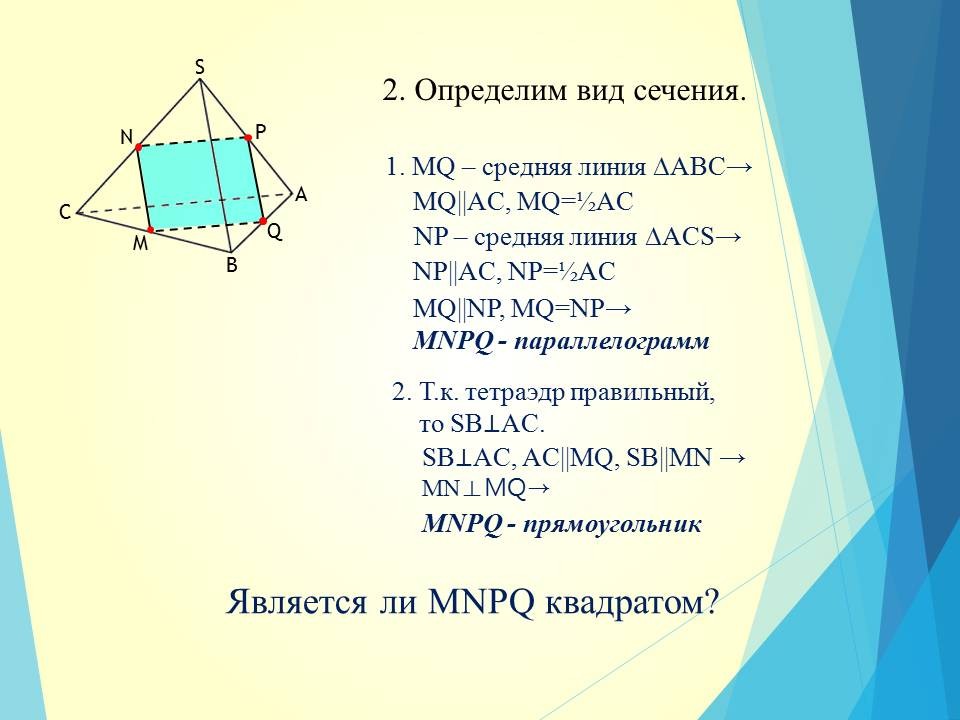
Задача 1.
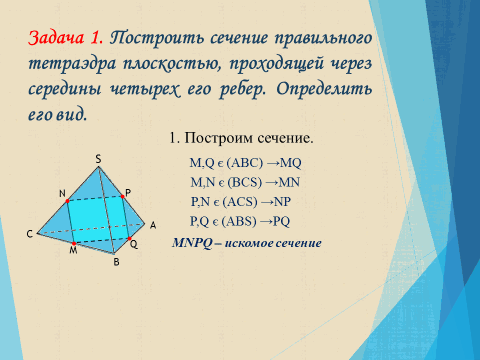

- Является ли прямоугольник MNPQ квадратом? Докажите это самостоятельно.
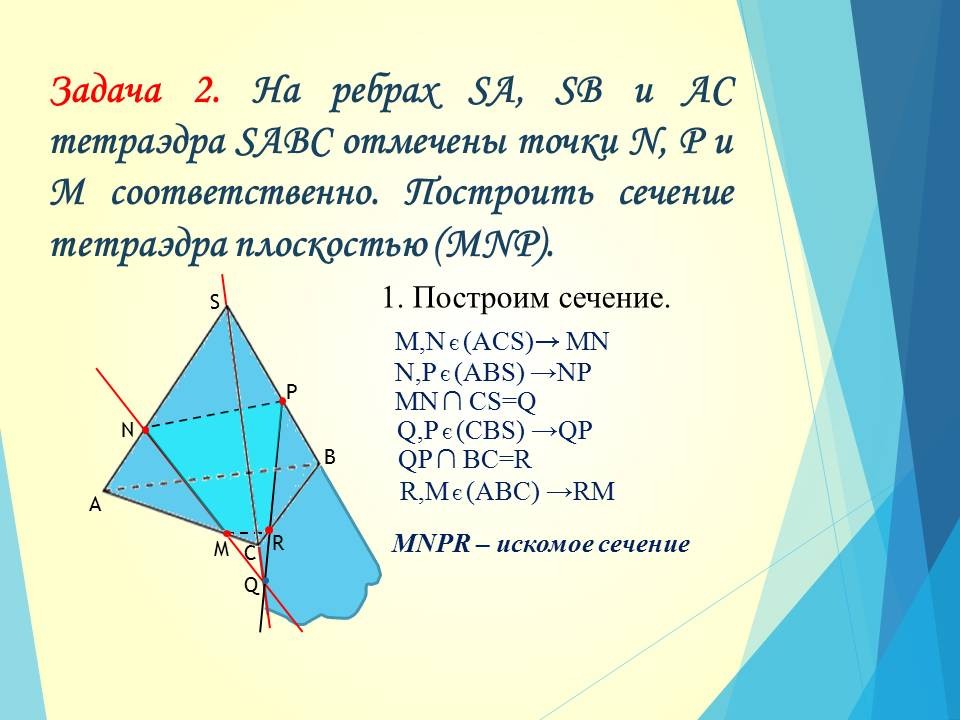
Задача 2.
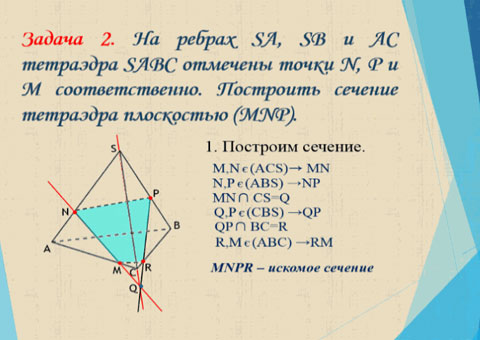
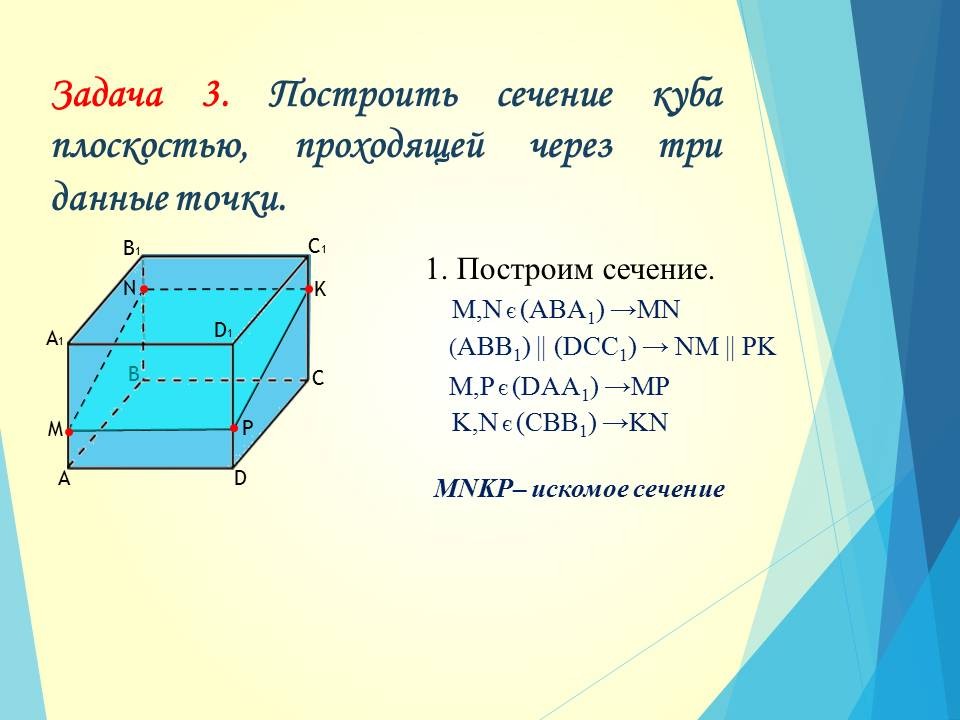
Задача 3.
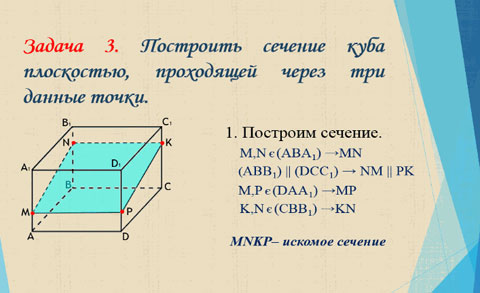
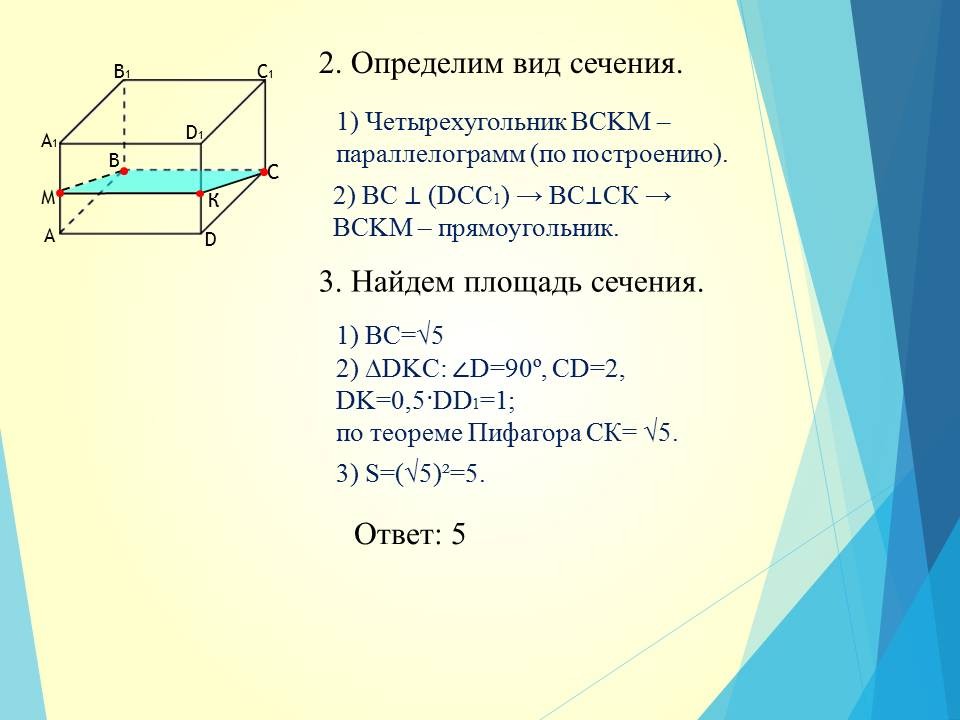
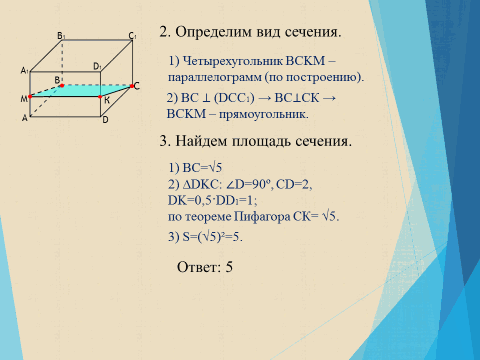
Задача, с которой был начат урок.
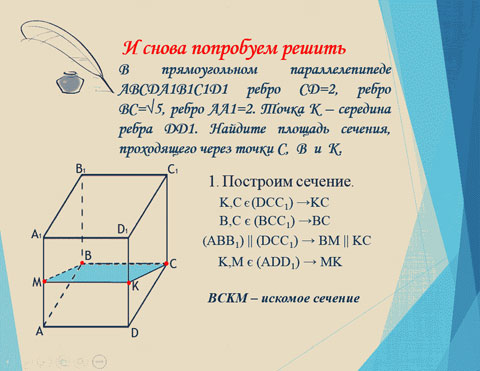
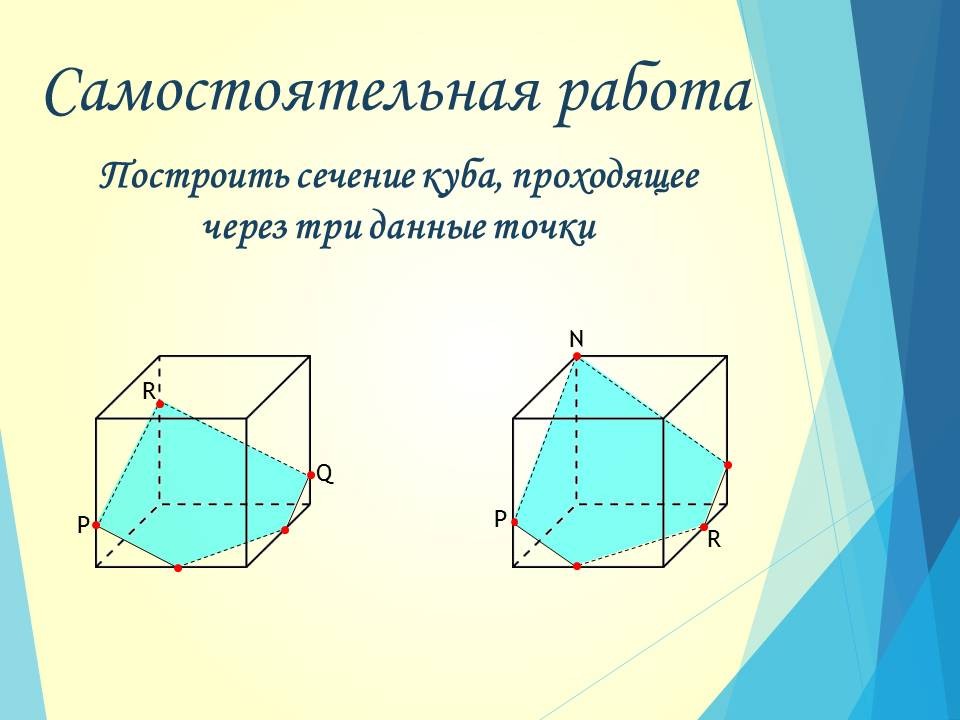
4. Самостоятельная работа
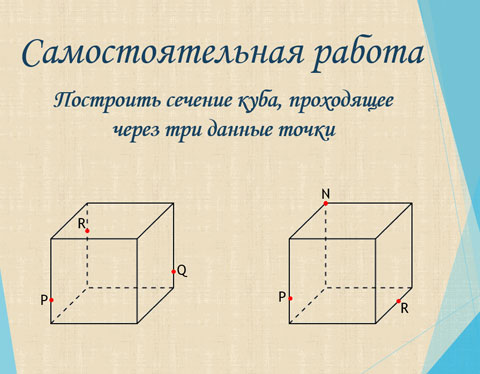
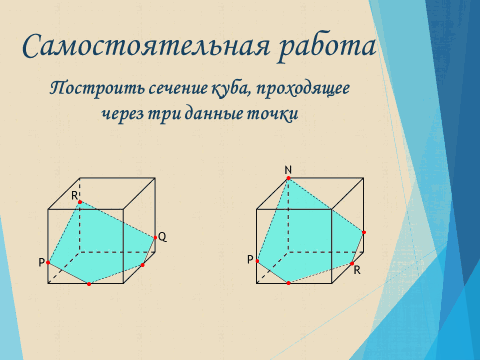
Проверка с помощью документ-камеры двух любых работ (по одной из каждого варианта), обсуждение ошибок, если таковые были допущены, сравнение с решением, предложенным учителем (остановиться на вариантах записи решения, обсудить, что является ошибкой, какие могут быть недочеты).
5. Рефлексия “Оцени себя на уроке”.
Учащимся дается индивидуальная карточка, в которой нужно подчеркнуть фразы, характеризующие работу ученика на уроке по трем направлениям. (Приложение 2)
Урок |
Я на уроке |
Итог |
| Интересно Скучно Безразлично |
Работал Отдыхал Помогал другим |
Понял материал Узнал больше, чем знал Не понял |
Информация о домашнем задании (Приложение 1)
Решить задачи 1-4.
Индивидуальное дополнительное задание (для более подготовленных учащихся и тех, кто хочет попробовать свои силы при решении более сложных задач) – задачи 5, 6.