Цели урока:
- образовательная: закрепить навыки работы с графиками функций; познакомить с алгоритмом нахождения наибольшего и наименьшего значений функции с применением производной; научить учащихся пользоваться этим алгоритмом.
- развивающая: развивать умение мыслить; развить навыки исследовательской и познавательной деятельности; развить навыки самопроверки; развить умение выполнять умственные операции: обобщение, сравнение, анализ, делать вывод.
- воспитывающая: воспитание устойчивого интереса к предмету, навыков коммуникативности, эстетических вкусов.
Ход урока
Актуализация знаний учащихся.
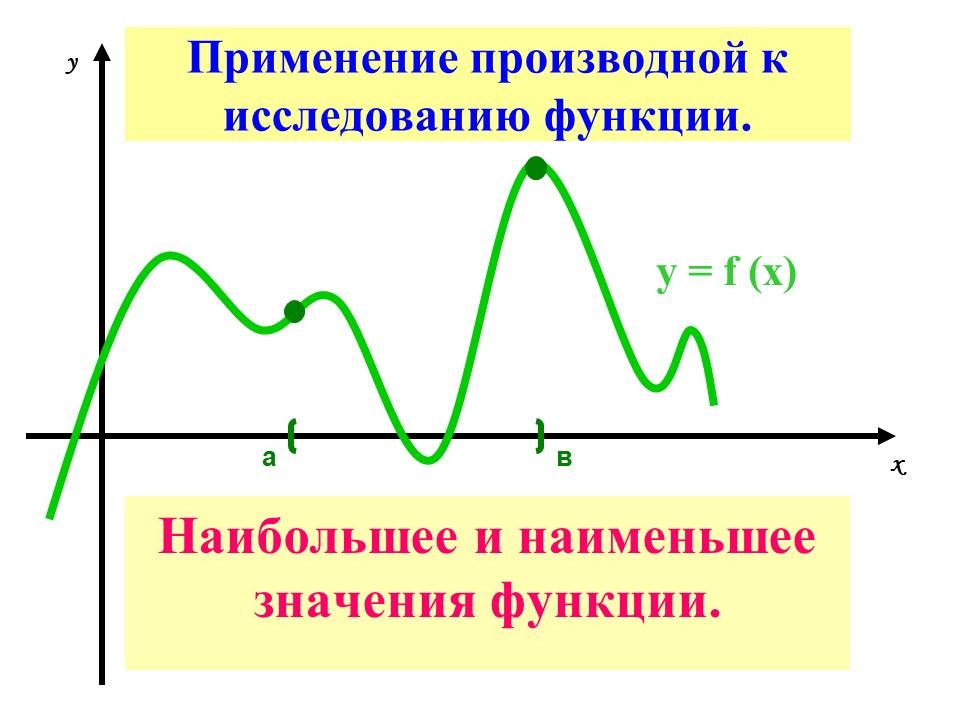
Вступительная беседа с учащимися. Слайды №1-6
Устная работа по готовым чертежам. Вопросы для повторения изученного материала.
1. Область определения функции.
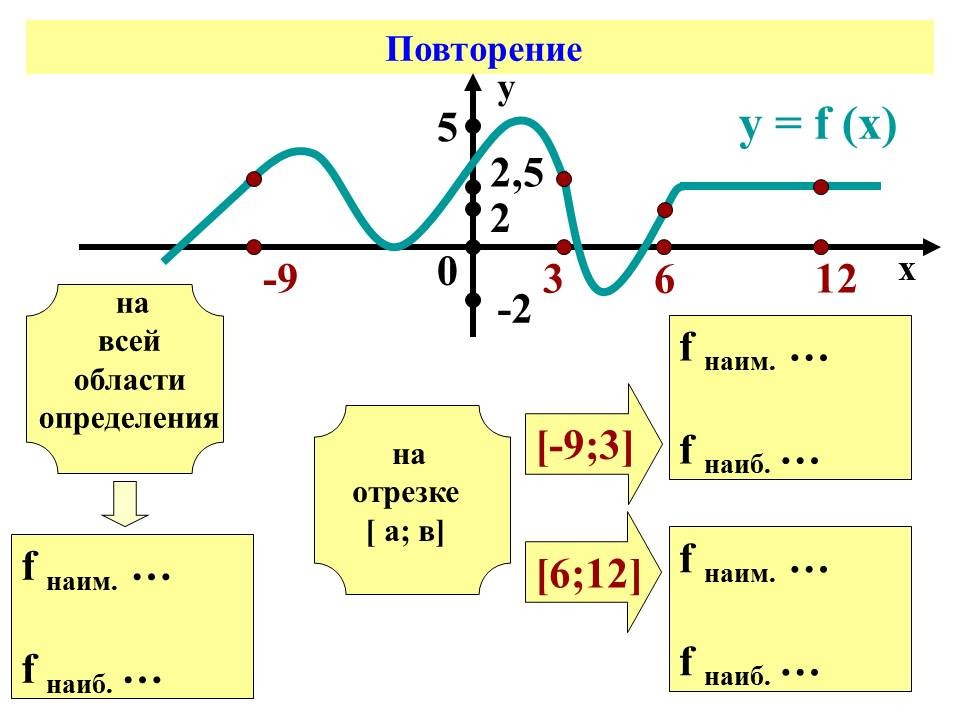
2. Множество значений функции. Слайд №7.
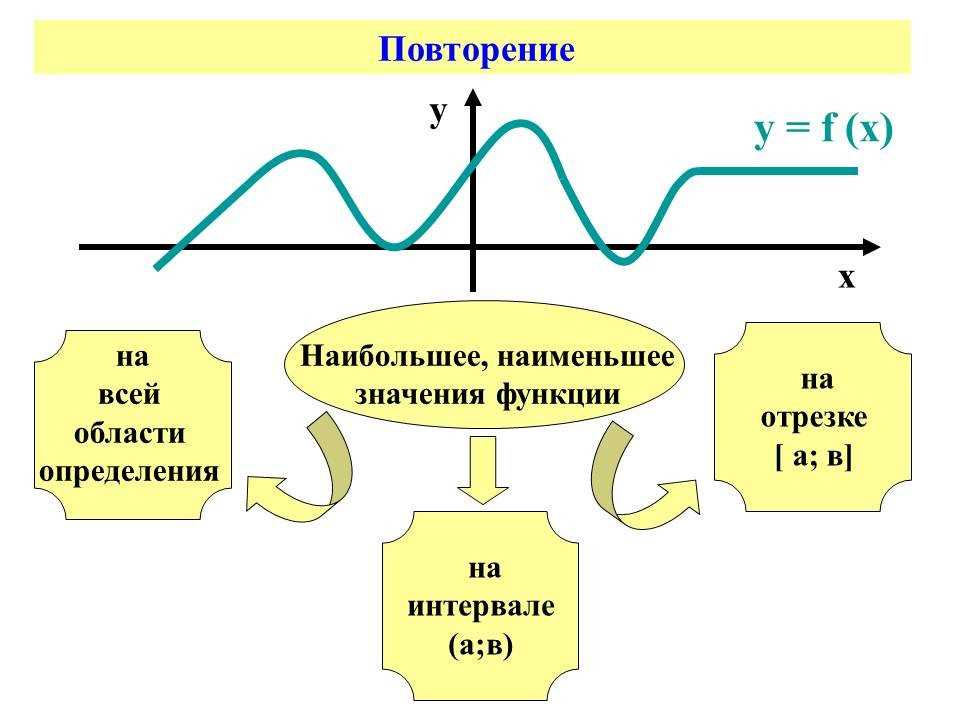
3. Наибольшее и наименьшее значения функции на
- всей области определения;
- интервале (а;в);
- отрезке [a;в].
Работа с графиком функции. Слайд №8.
Постановка проблемы для установления зависимости между наибольшим и наименьшим значениями функции, значениями функции на концах отрезка, значением функции в критических точках заданного промежутка.
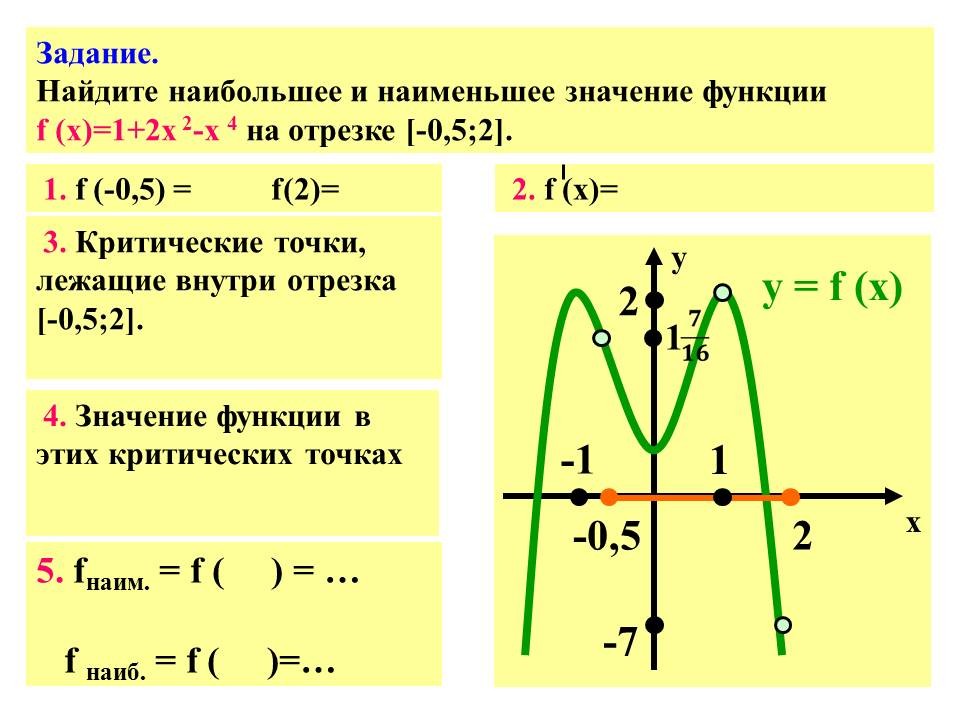
Задание. Найти наибольшее и наименьшее значения функции f(x)=2х2-х4+1 на отрезке [-0,5;2]. Можно ли дать ответ на этот вопрос, не выполняя построения графика функции? Слайд №9.
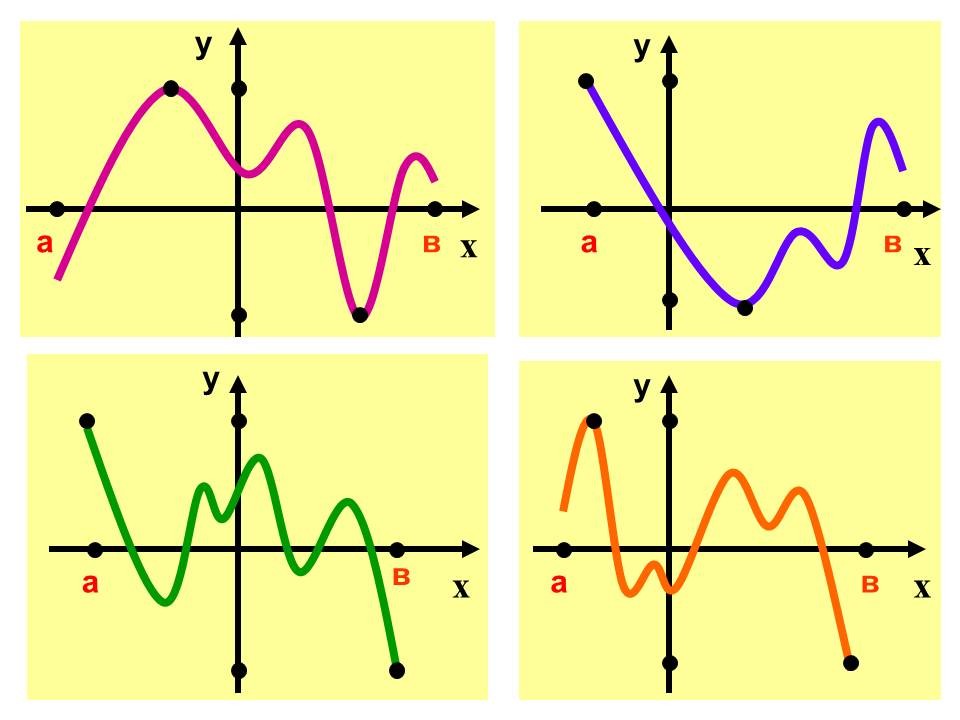
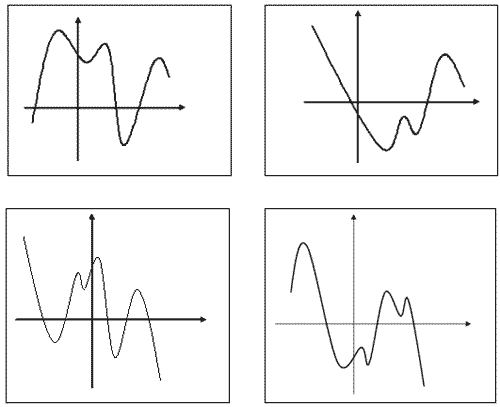
- Поисковая работа учащихся по установлению зависимости между наибольшим и наименьшим значениями функции, значениями функции на концах отрезка, значением функции в критических точках заданного промежутка. Слайд№10.
- 1-й чертеж: f наим.=f(х1), х=х1 - точка минимума; f наиб.=f(х2), х=х2 - точка максимума
- 2-й чертеж: f наим.=f(х1), х=х1 - точка минимума; f наиб.=f(а)
- 3-й чертеж: f наиб.=f(а); f наим.=f(в)
- 4-й чертеж: f наиб.=f(х1), х=х1 - точка максимума; f наим.=f(в)
- “Открытие” зависимости между наибольшим и наименьшим значениями функции, значениями функции на концах отрезка, значением функции в критических точках заданного промежутка.
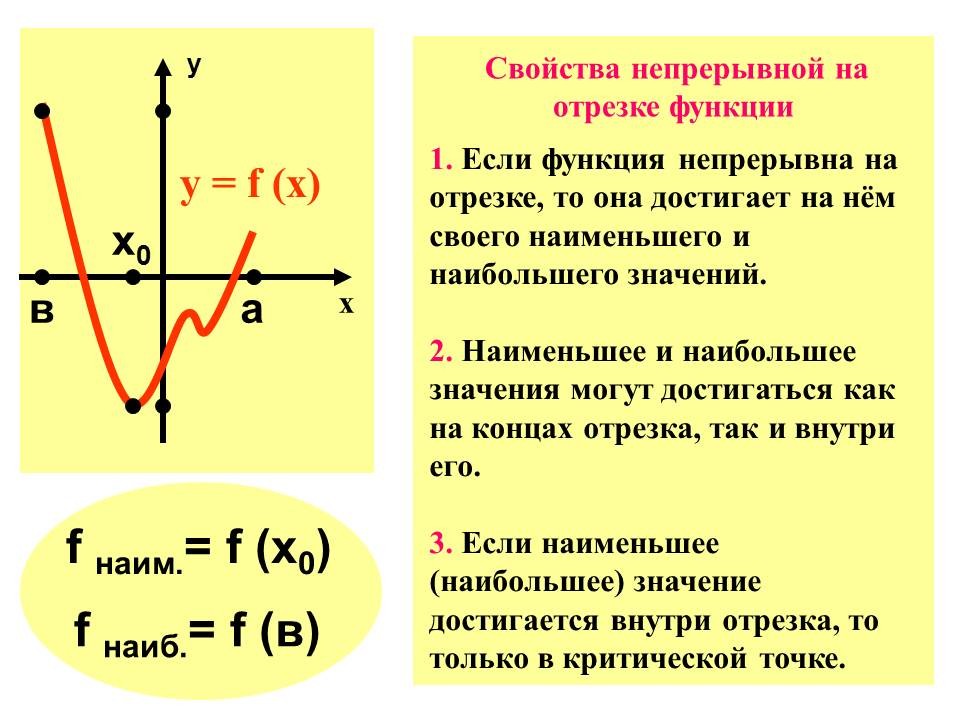
- Обобщение полученных знаний. Формулирование свойств непрерывной функции. Слайд№11.
1. Если функция непрерывна на отрезке, то она достигает на нём своего наименьшего и наибольшего значений.
2. Наименьшее и наибольшее значения могут достигаться как на концах отрезка, так и внутри его.
3. Если наименьшее (наибольшее) значение достигается внутри отрезка, то только в критической точке.
- Алгоритм нахождения наибольшего и наименьшего значений функции. Слайд № 12 .
Закрепление изученного материала.
Решение задания.
Найти наибольшее и наименьшее значения функции f(x)=2х2-х4+1 на отрезке [-0,5;2]. Слайд№13.
Итоги урока. Слайд № 14.
План-конспект для учеников
Тема урока: “Наибольшее и наименьшее значения функции”.
Свойства непрерывной на отрезке функции.
______________________________________
______________________________________
______________________________________
В каких точках функция принимает наибольшее и наименьшее значения на отрезке [ а; в ]?
Алгоритм нахождения наибольшего и наименьшего значений функции.
______________________________________
______________________________________
______________________________________