Цели урока:
- образовательная: повторить определение критических точек; закрепить навыки работы с графиками функций; познакомить с необходимым и достаточным условиями экстремума функции ; научить учащихся находить экстремумы функции.
- развивающая: развивать умение мыслить; развить навыки исследовательской и познавательной деятельности; развить навыки самопроверки; развить умение выполнять умственные операции: обобщение, сравнение, анализ, делать вывод.
- воспитывающая: воспитание устойчивого интереса к предмету, навыков коммуникативности, эстетических вкусов.
Ход урока
Актуализация знаний учащихся.
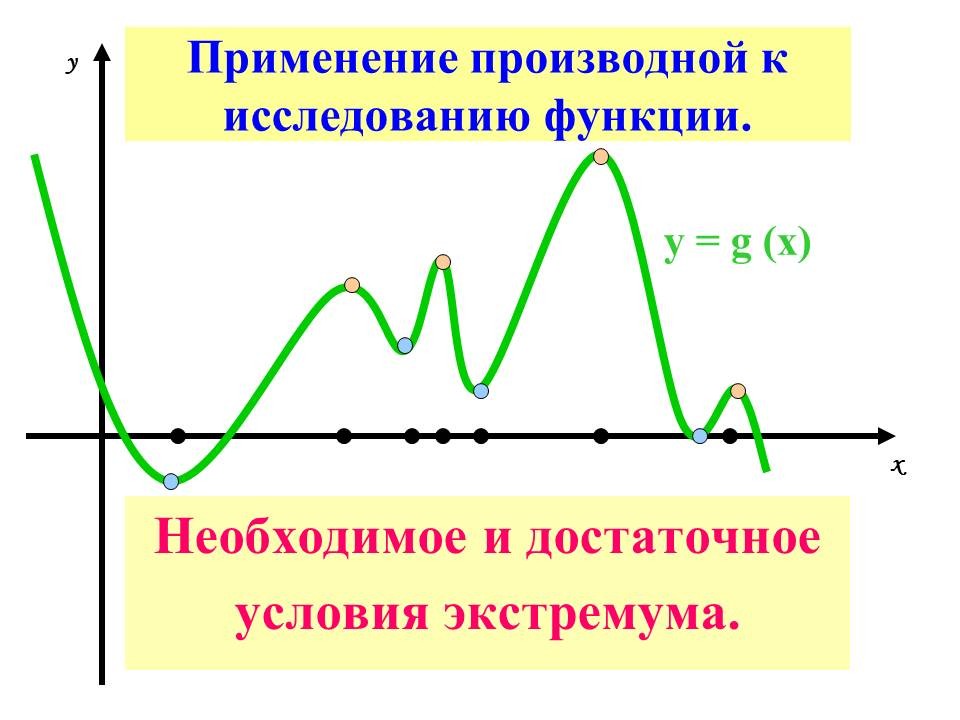
Вступительное слово учителя. Слайды №1,2.
Устная работа по готовым чертежам. Вопросы для повторения изученного материала.
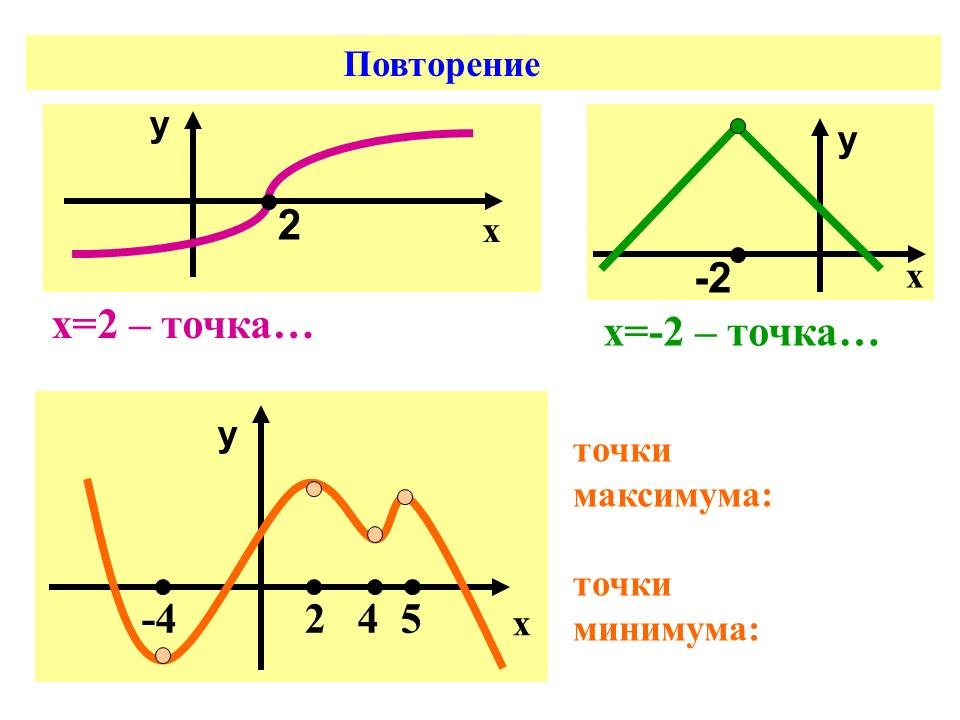
1. Повторение теории. Слайд №3.
2. Работа с графиками функций. Нахождение по графику критических точек функции и экстремумов функции. Слайд № 4.
Постановка проблемы по установлению необходимых и достаточных условий экстремума и работа по ее решению.
Как найти экстремумы функции, не выполняя построения графика функции? Слайд № 5.
1. Необходимое условие экстремума.
- Исследовательская работа учащихся по “открытию” необходимого условия экстремума.
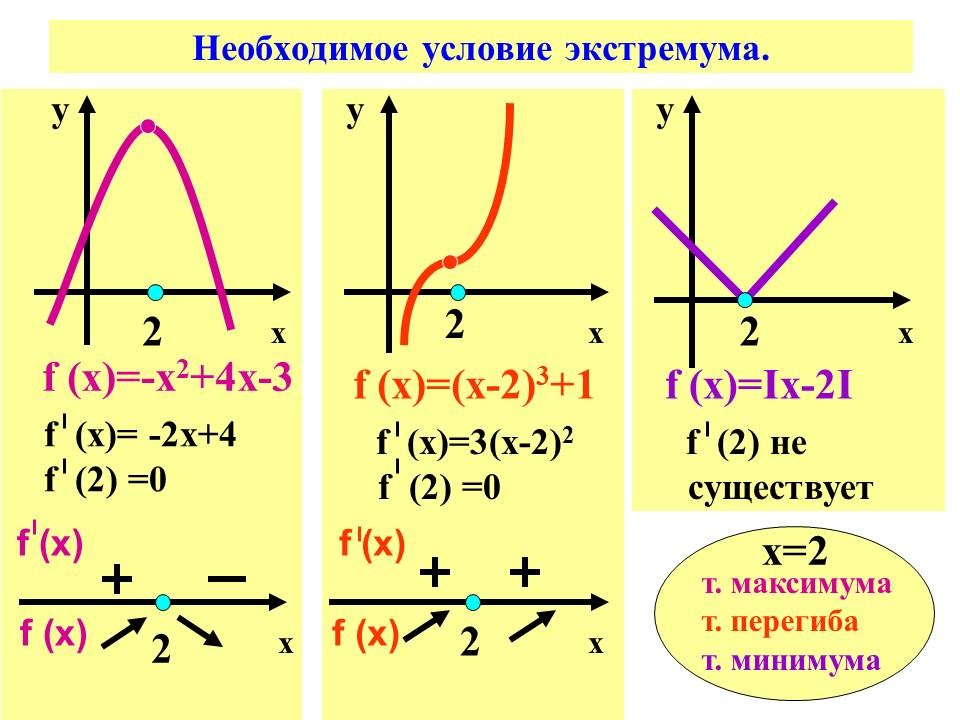
Рассматривается функция f ( х ) = -х2 +4х-3: f ' ( х ) = -2х+4, f ' ( 2 ) =0, выполнение чертежа, связывающего значение производной функции и название точки х=2.
Рассматривается функция f ( х ) = ( х-2) 3 + 1: f ' ( х ) = 3 ( х-2 ) 2, f ' ( 2 ) = 0, выполнение чертежа, связывающего значение производной функции и название точки х=2.
Рассматривается функция f ( х ) = | х – 2|: f ' ( х ) не существует в точке х = 2.
Вывод по исследованиям: в точке х=2 производная равна нулю или не существует; точка х=2 является точкой максимума, точкой перегиба, точкой минимума. Слайды № 6.
“Открытие” и формулировка необходимых условий экстремума. Слайды № 7.
2. Достаточные условия экстремума.
Исследовательская работа учащихся по “открытию” достаточных условий экстремума.
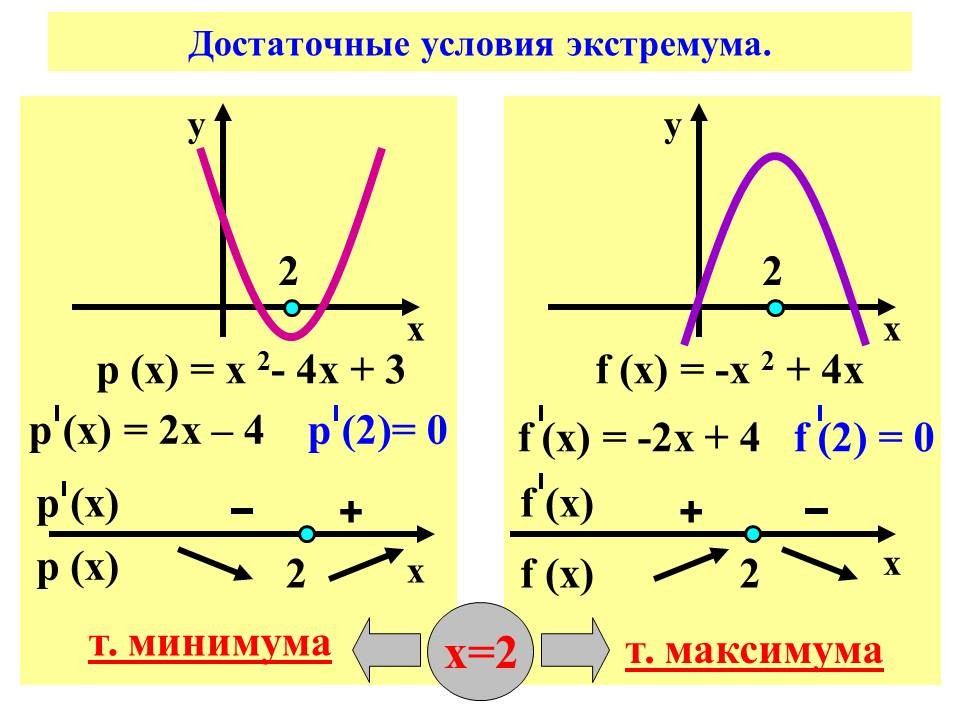
Рассматривается функция р ( х ) = х 2 -4х +3 :
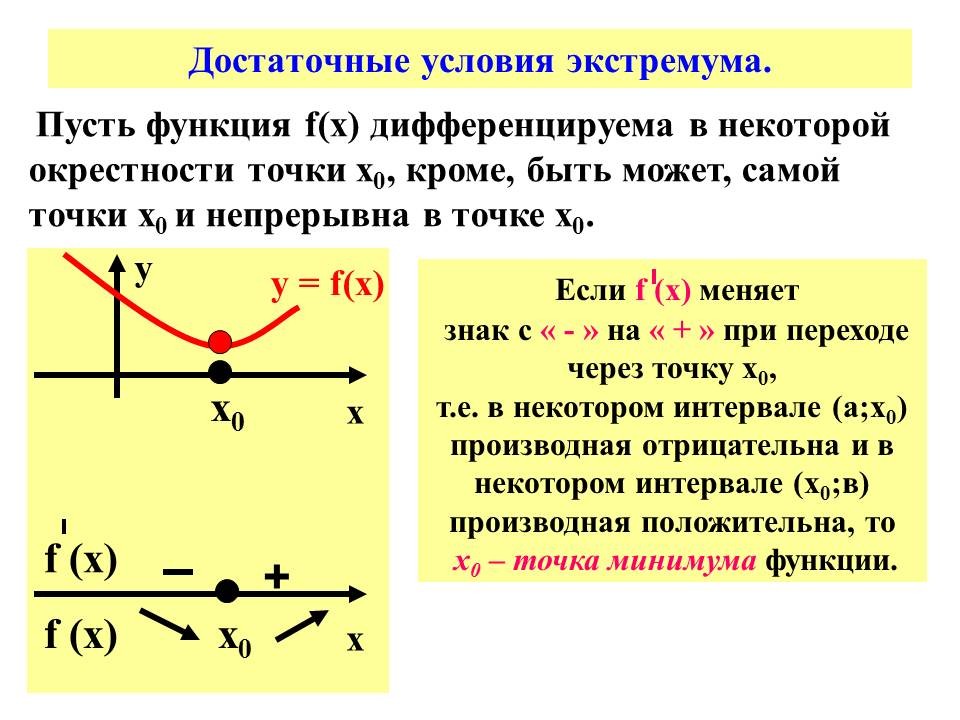
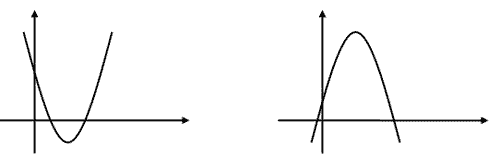
р ' ( х ) = 2х -4 , р ' ( 2 ) = 0, выполнение чертежа, связывающего знак производной функции и характер ее монотонности, х = 2 – точка минимума функции.
Рассматривается функция f ( х ) =- х 2 +4х :
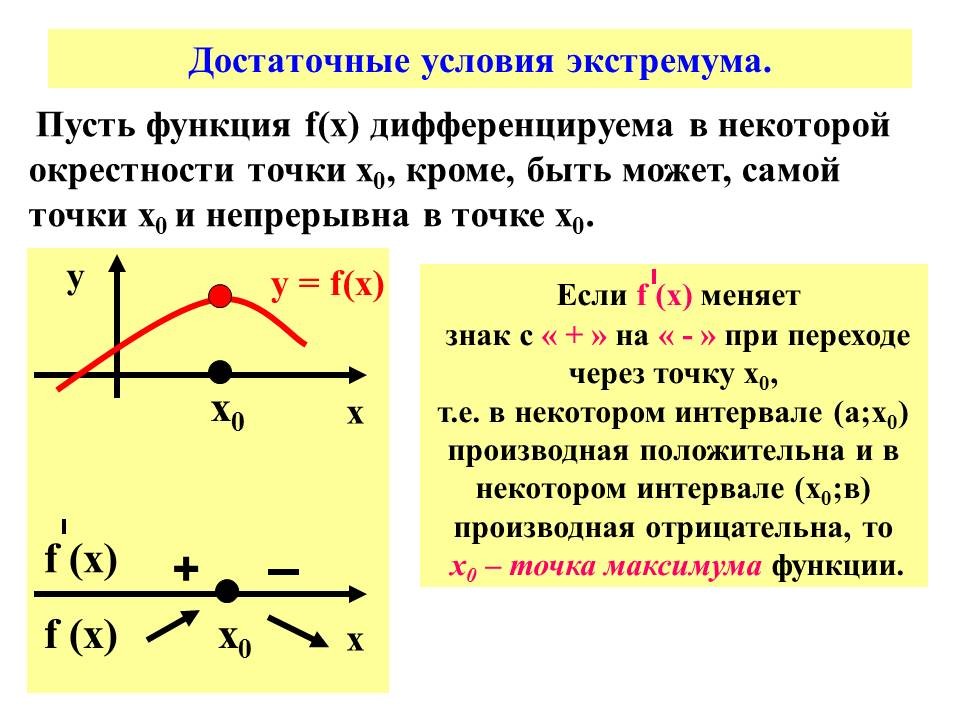
f ' ( х ) = -2х + 4 , f ' ( 2 ) = 0, выполнение чертежа, связывающего знак производной функции и характер ее монотонности, х = 2 – точка максимума функции.
Вывод по исследованиям, “открытие” достаточных условий экстремума. Слайд № 8.
Обобщение знаний, формулировка достаточных условий экстремума. Слайды №№ 9; 10.
- Алгоритм исследования функции на монотонность и экстремумы. Слайд № 11.
Закрепление изученного материала.
Решение заданий.
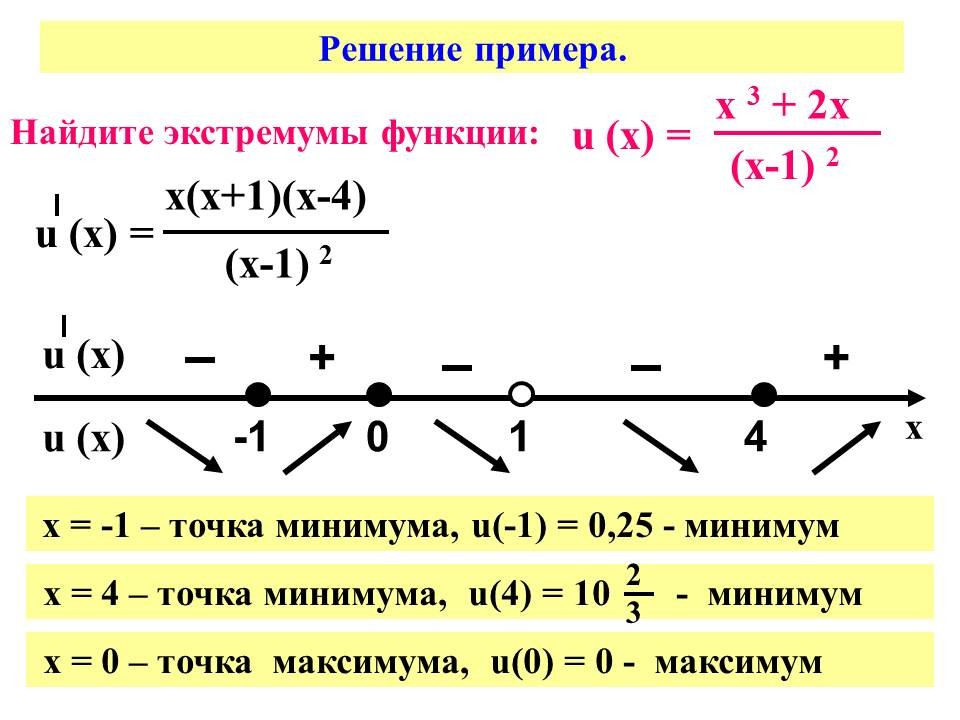
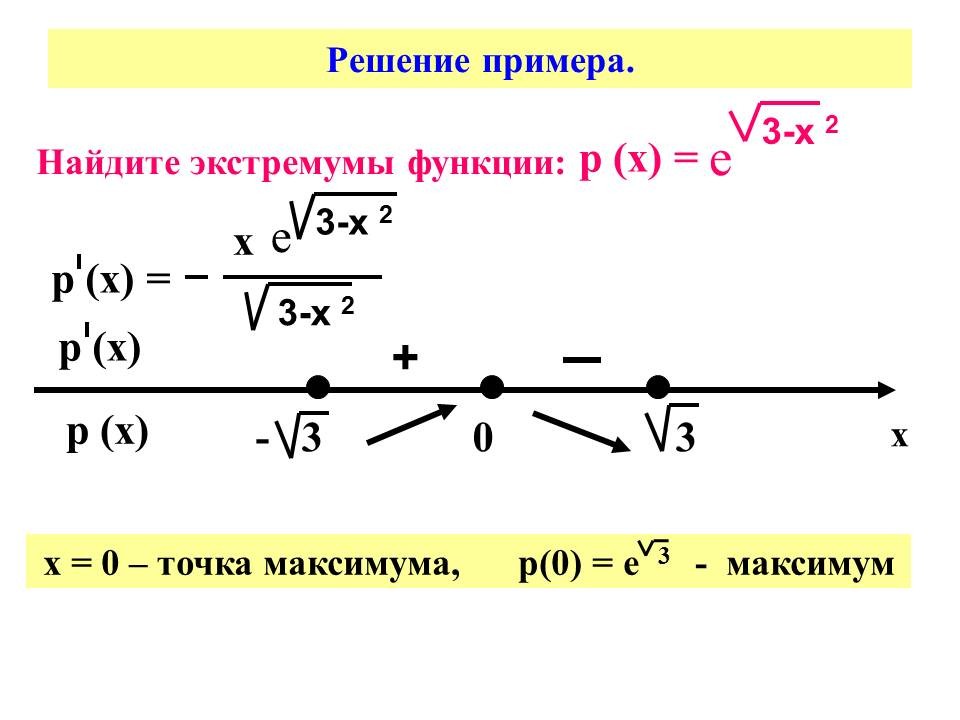
Найдите экстремумы функции.
u (х) = (х 3 + 2х ) / ( х -1) 2 Слайд №12 .
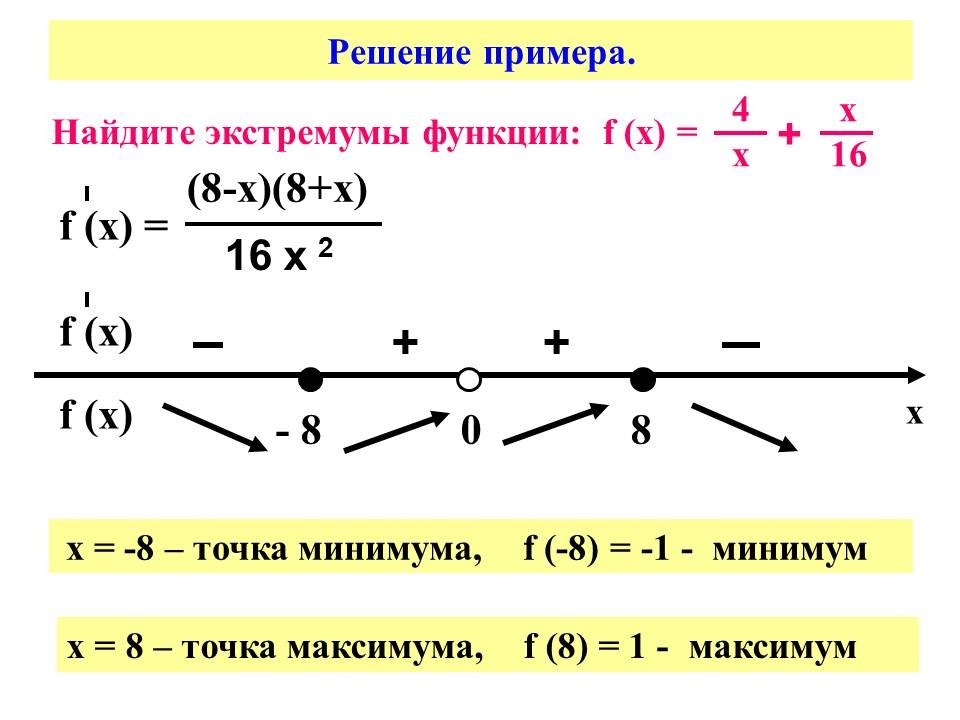
f (х) = 4/ х + х/ 16 Слайд № 13.
р(х) = ![]() Слайд № 14 .
Слайд № 14 .
Итоги урока.
Слайд №15 .
План-конспект для ученика. Тема урока: “Необходимое и достаточное условия экстремума функции”.
1. Необходимые условия экстремума.

_________________________________________
_________________________________________
2. Достаточные условия экстремума.
._________________________________________
__________________________________________
3. Алгоритм исследования функции на монотонность и экстремумы.
___________________________________________
____________________________________________