Цели и задачи:
Образовательные:
- повторить и обобщить знания о треугольнике;
- доказать теорему о сумме углов треугольника;
- практически убедиться в правильности формулировки теоремы;
- научиться применять полученные знания при решении задач.
Развивающие:
- развивать геометрическое мышление, интерес к предмету, познавательную и творческую деятельность учащихся, математическую речь, умение самостоятельно добывать знания.
Воспитательные:
- развивать личностные качества учащихся, таких как целеустремленность, настойчивость, аккуратность, умение работать в коллективе.
Оборудование: мультимедийный проектор, треугольники из цветной бумаги, УМК «Живая математика», компьютер, экран.
Подготовительный этап: учитель дает задание ученику подготовить историческую справку о теореме «Сумма углов треугольника».
Тип урока: изучение нового материала.
Ход урока
I. Организационный момент
Приветствие. Психологический настрой учащихся на работу.
II. Разминка
С геометрической фигурой “треугольник” мы познакомились на предыдущих уроках. Давайте повторим, что нам известно о треугольнике?
Учащиеся работают по группам. Им предоставлена возможность общаться друг с другом, каждому самостоятельно строить процесс познания.
Что получилось? Каждая группа высказывает свои предложения, учитель записывает их на доске. Проводится обсуждение результатов:
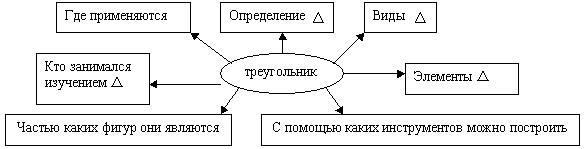
Рисунок 1
III. Формулируем задачу урока
Итак, о треугольнике мы знаем уже достаточно много. Но не все. У каждого из вас на парте есть треугольники и транспортиры. Как вы думаете, какую задачу мы можем сформулировать?
Ученики формулируют задачу урока - найти сумму углов треугольника.
IV. Объяснение нового материала
Практическая часть (способствует актуализации знаний и навыков самопознания). Проведите измерения углов с помощью транспортира и найдите их сумму. Результаты запишите в тетрадь (заслушать полученные ответы). Выясняем, что сумма углов у всех получилась разная (так может получиться, потому что неточно приложили транспортир, небрежно выполнили подсчет и т.д.).
Выполните перегибания по пунктирным линиям и узнайте, чему еще равна сумма углов треугольника:
а)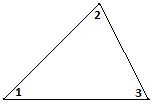
Рисунок 2
б) 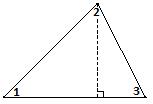
Рисунок 3
в) 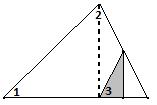
Рисунок 4
г) 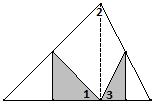
Рисунок 5
д) 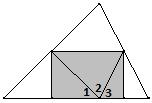
Рисунок 6
После выполнения практической работы ученики формулируют ответ: Сумма углов треугольника равна градусной мере развернутого угла, т. е. 180°.
Учитель: В математике практическая работа дает возможность лишь сделать какое-то утверждение, но его нужно доказать. Утверждение, справедливость которого устанавливается путем доказательства, называется теоремой. Какую теорему мы можем сформулировать и доказать?
Ученики: Сумма углов треугольника равна 180 градусов.
Историческая справка: Свойство суммы углов треугольника было установлено еще в Древнем Египте. Доказательство, изложенное в современных учебниках, содержится в комментариях Прокла к «Началам» Евклида. Прокл утверждает, что это доказательство (рис. 8) было открыто еще пифагорейцами (5 в. до н. э.). В первой книге «Начал» Евклид излагает другое доказательство теоремы о сумме углов треугольника, которое легко понять при помощи чертежа (рис. 7):
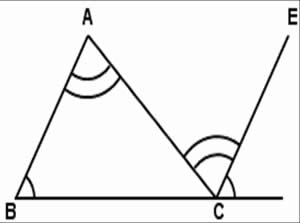
Рисунок 7
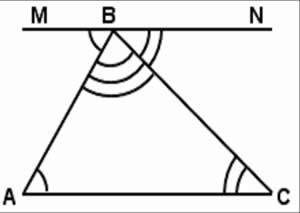
Рисунок 8
Чертежи высвечиваются на экране через проектор.
Учитель предлагает с помощью чертежей доказать теорему.
Затем доказательство проводится с применением УМК «Живая математика». Учитель на компьютере проецирует доказательство теоремы.
Теорема о сумме углов треугольника: «Сумма углов треугольника равна 180°»
Рисунок 9
Доказательство:
а) 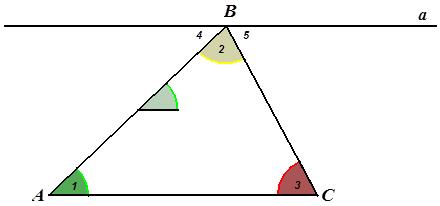
Рисунок 10
б) 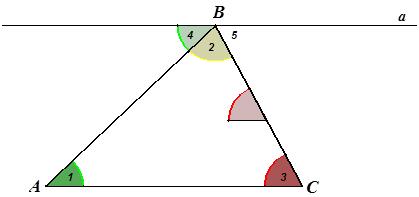
Рисунок 11
в) 
Рисунок 12
Учащиеся в тетради делает краткую запись доказательства теоремы:
Теорема: Сумма углов треугольника равна 180°.
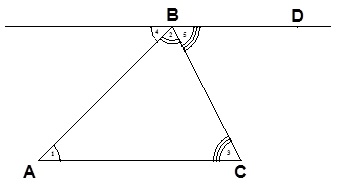
Рисунок 13
Дано: Δ АВС
Доказать: ![]() А +
А + ![]() В +
В + ![]() С = 180°.
С = 180°.
Доказательство:
- Проведем через вершину В прямую ВD, параллельную АС;
 1 =
1 =  4 как накрест лежащие, так как ВD || АС и АВ – секущая;
4 как накрест лежащие, так как ВD || АС и АВ – секущая; 3 =
3 =  5 как накрест лежащие, так как ВD || АС и ВС – секущая;
5 как накрест лежащие, так как ВD || АС и ВС – секущая; 4,
4,  2 и
2 и  5 составляют развернутый угол;
5 составляют развернутый угол; 4 +
4 +  2 +
2 +  5 = 180°, так как градусная мера развернутого угла равна 180°.
5 = 180°, так как градусная мера развернутого угла равна 180°. 1+
1+  2 +
2 +  3 = 180° или
3 = 180° или  А +
А +  В +
В +  С = 180°.
С = 180°.
Что требовалось доказать.
V. Физ. минутка.
VI. Объяснение нового материала (продолжение)
Следствие из теоремы о сумме углов треугольника выводится учащимися самостоятельно, это способствует развитию умения формулировать собственную точку зрения, высказывать и аргументировать ее:
В любом треугольнике либо все углы острые, либо два острых угла, а третий тупой или прямой.
Если в треугольнике все углы острые, то он называется остроугольным.
Если один из углов треугольника тупой, то он называется тупоугольным.
Если один из углов треугольника прямой, то он называется прямоугольным.
Теорема о сумме углов треугольника позволяет классифицировать треугольники не только по сторонам, но и по углам. (По ходу введения видов треугольников учащимися заполняется таблица)
Таблица 1
| Вид треугольника | Равнобедренный | Равносторонний | Разносторонний |
| Прямоугольный | 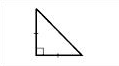 |
 |
|
| Тупоугольный | 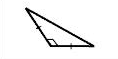 |
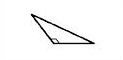 |
|
| Остроугольный | 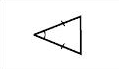 |
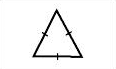 |
 |
VII. Закрепление изученного материала.
- Решить задачи устно:
(Чертежи высвечиваются на экране через проектор)
Задача 1. Найдите угол С.
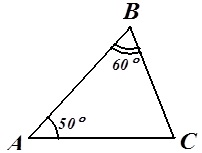
Рисунок 14
Задача 2. Найдите угол F.
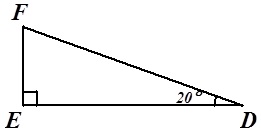
Рисунок 15
Задача 3. Найдите углы К и N.
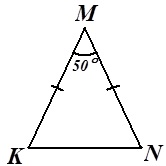
Рисунок 16
Задача 4. Найдите углы P и T.
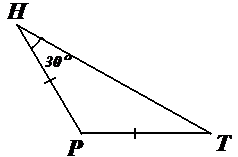
Рисунок 17
- Решить задачу самостоятельно № 223 (б, г).
- Решить задачу на доске и в тетрадях уч-ся №224.
- Вопросы: Может ли треугольник иметь: а) два прямых угла; б) два тупых угла; в) один прямой и один тупой угол.
- (выполняется устно) На карточках, имеющихся на каждом столе, изображены различные треугольники. Определите на глаз вид каждого треугольника.

Рисунок 18
- Найдите сумму углов 1, 2 и 3.
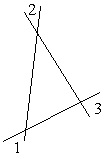
Рисунок 19
VIII. Итог урока.
Учитель: Что мы узнали? Для любого ли треугольника применима теорема?
IX. Рефлексия.
Передайте мне свое настроение, ребята! С обратной стороны треугольника изобразите свою мимику.
![]()
Рисунок 20
Домашнее задание: п.30 (1 часть), вопрос 1 гл. IV стр. 89 учебника; № 223 (а, в), № 225.