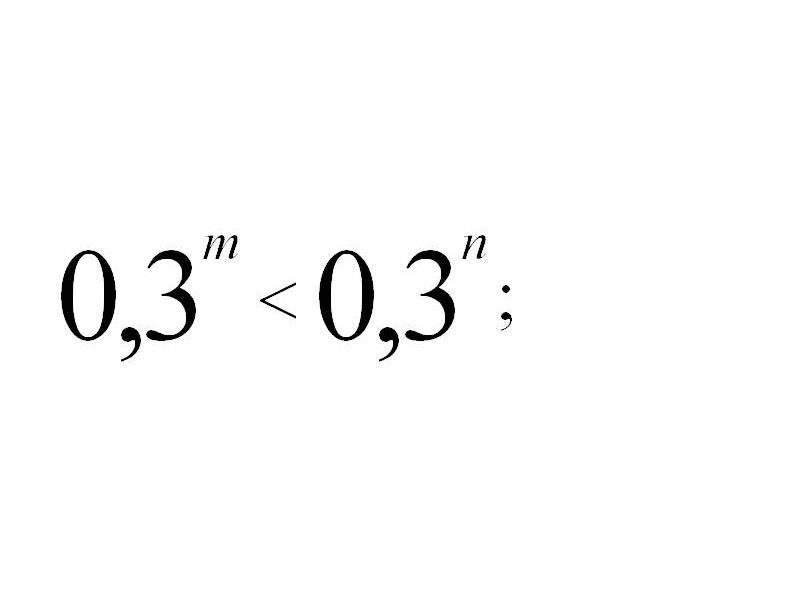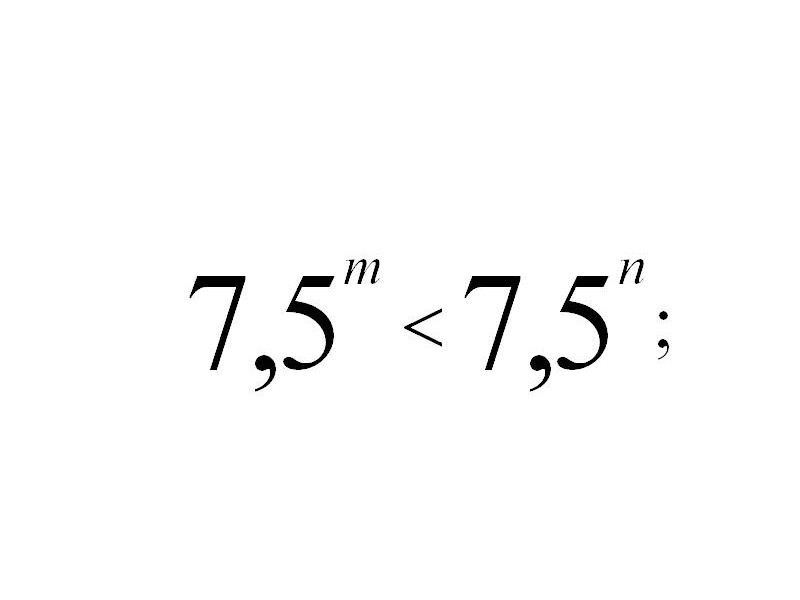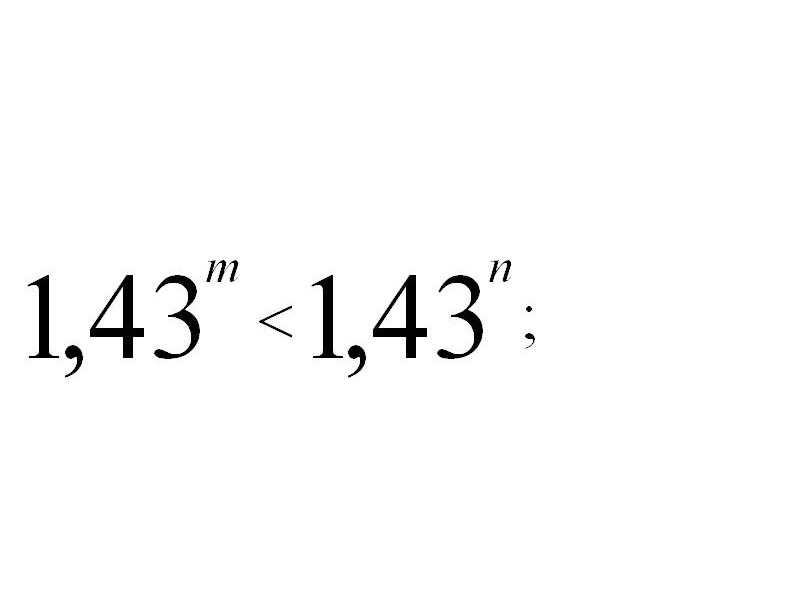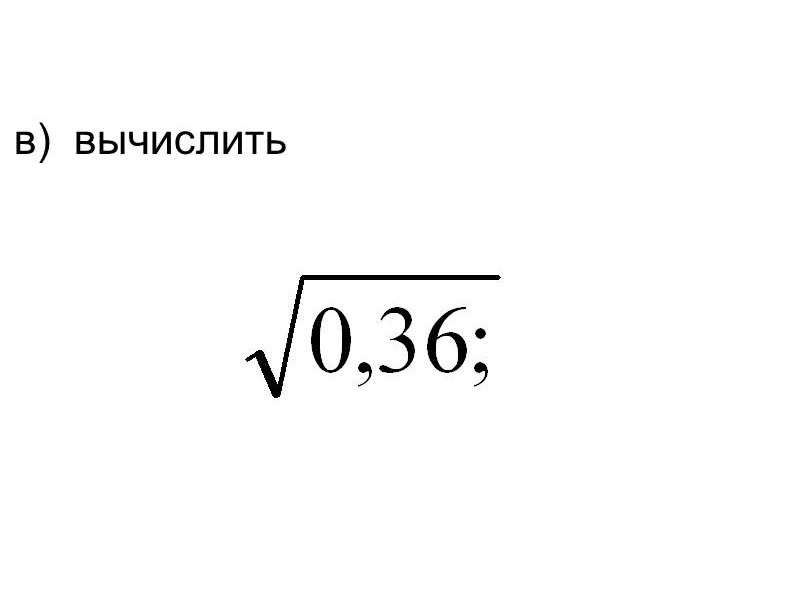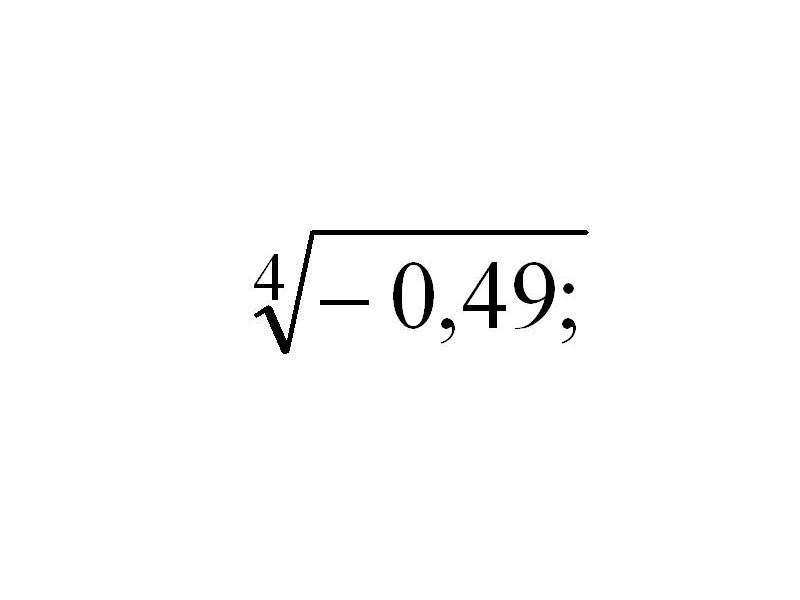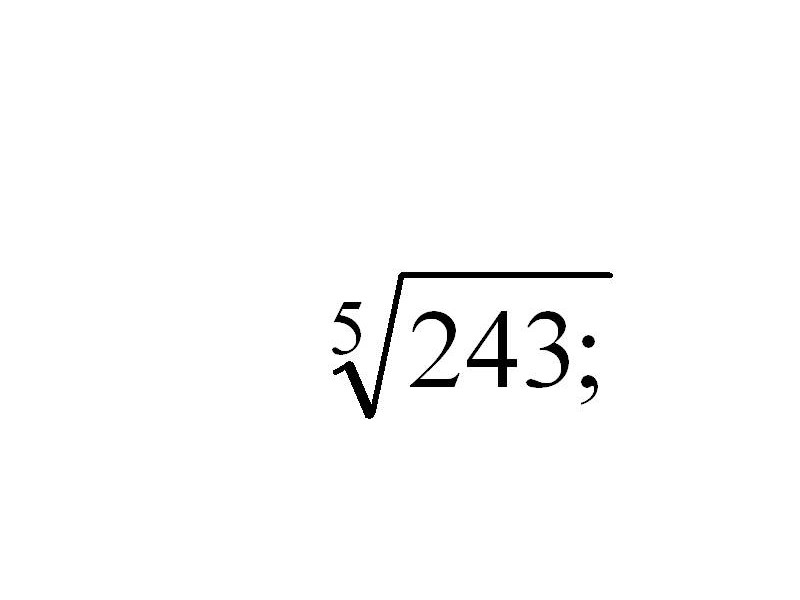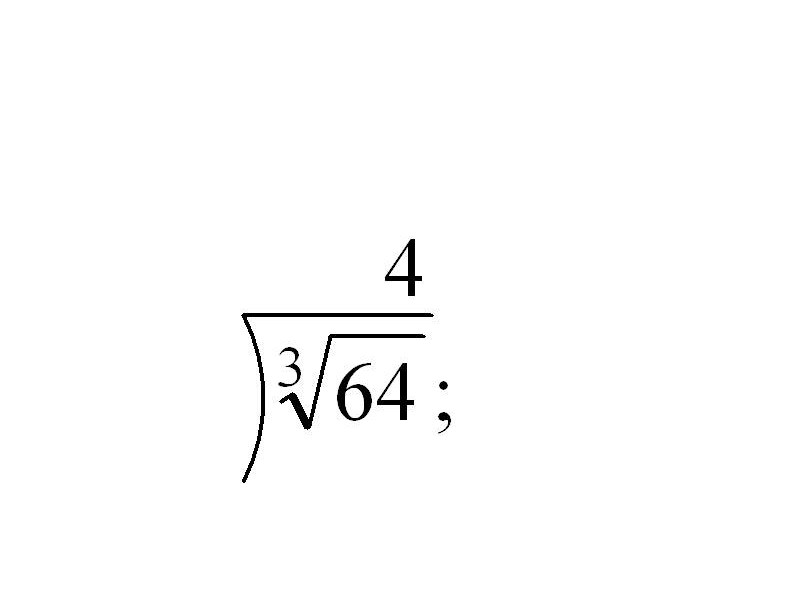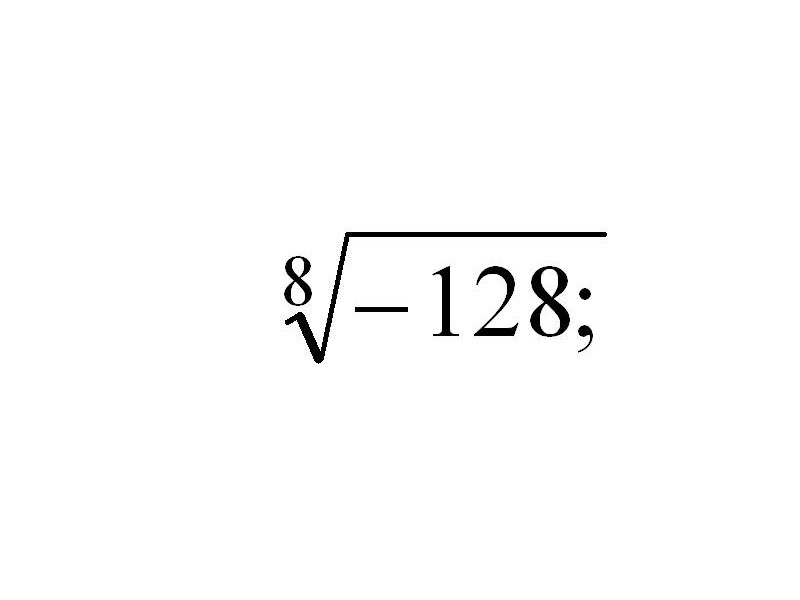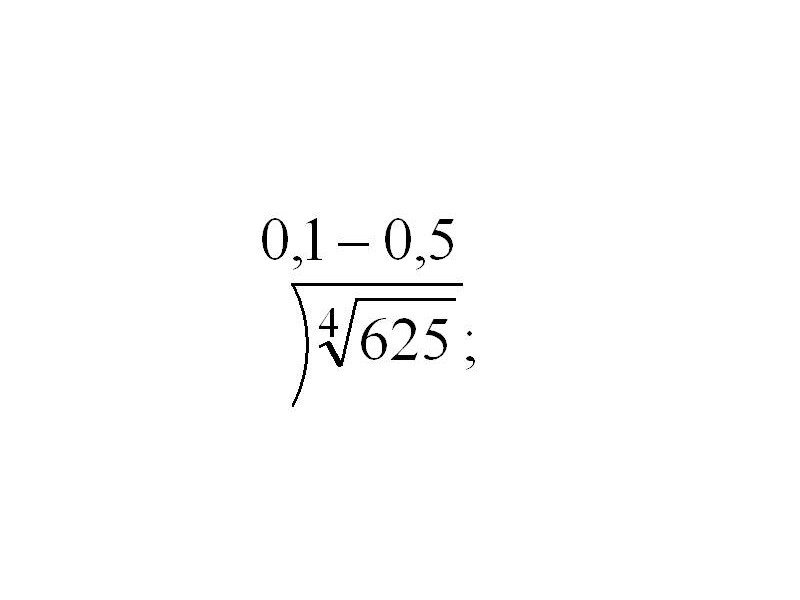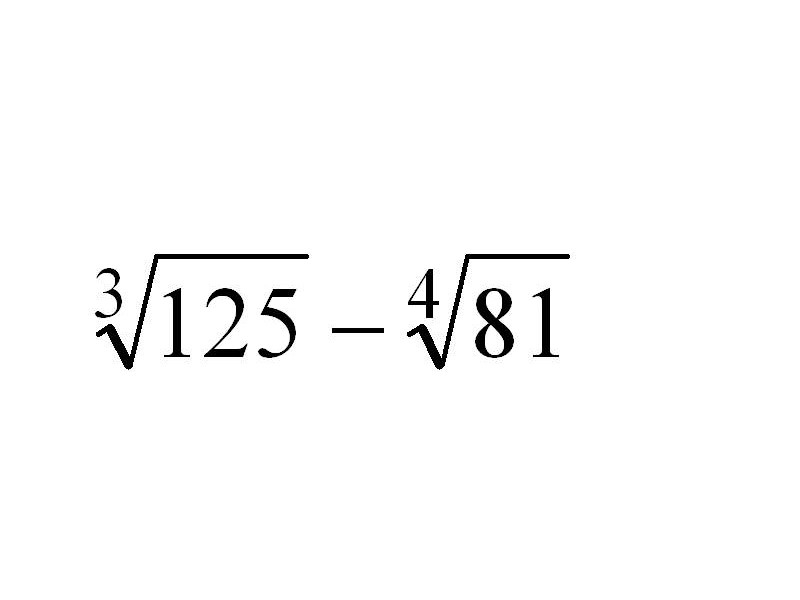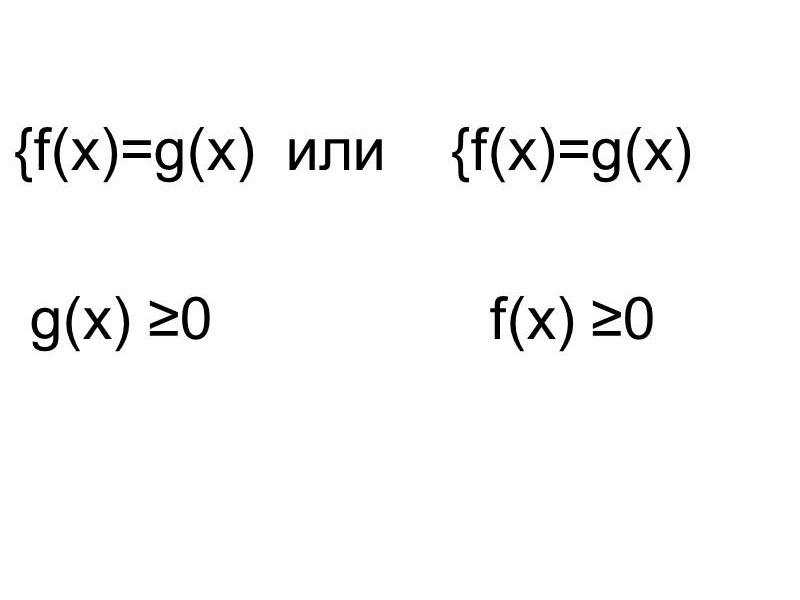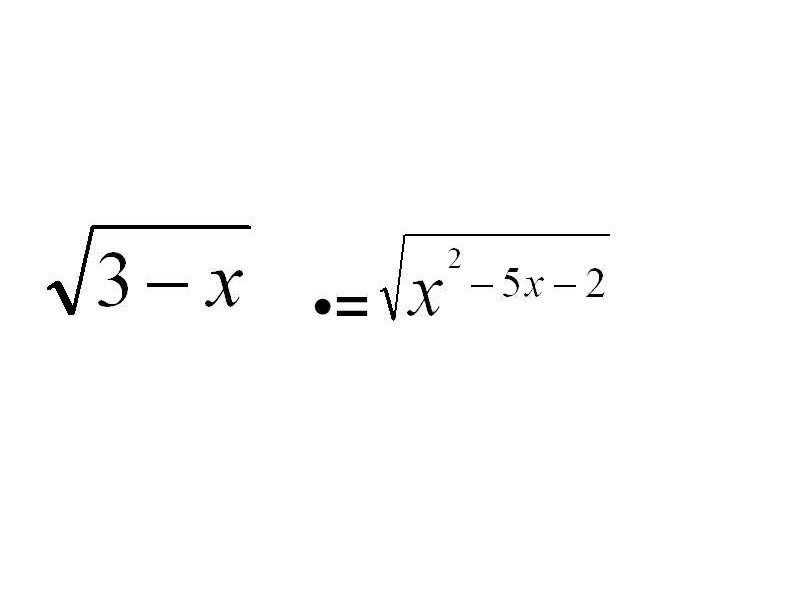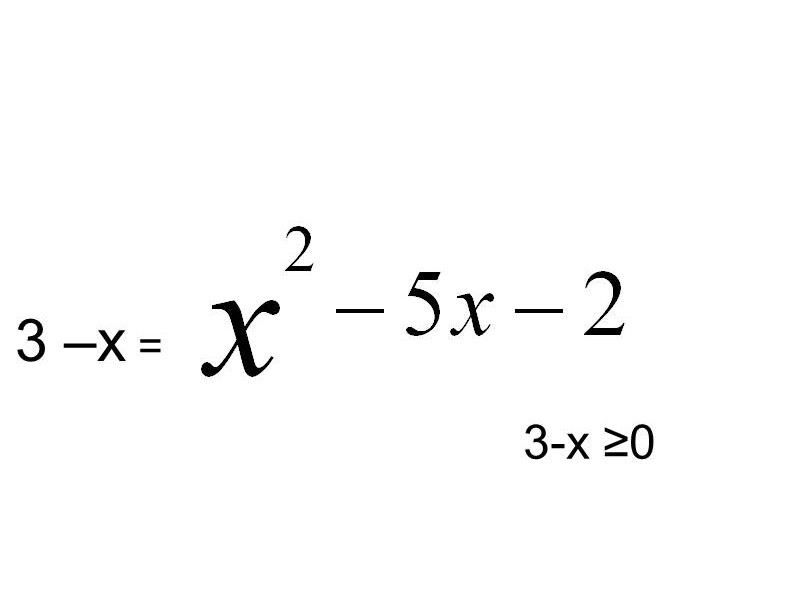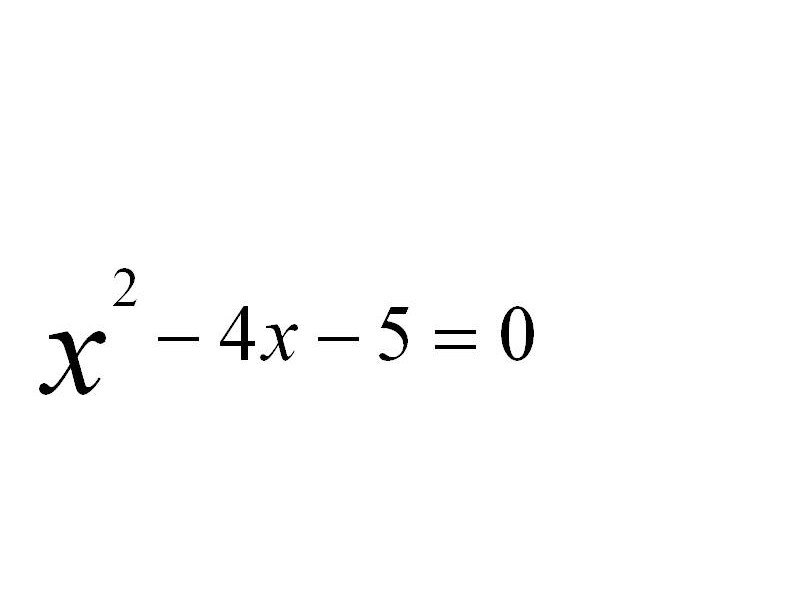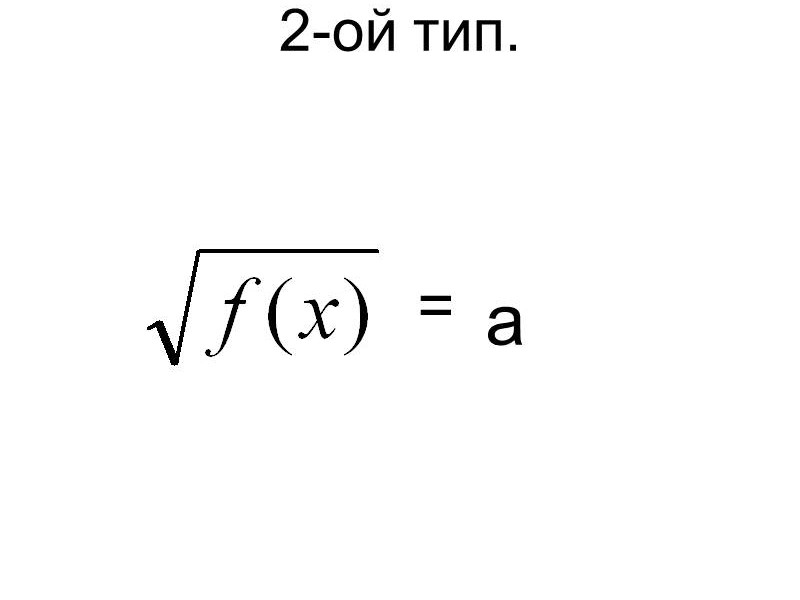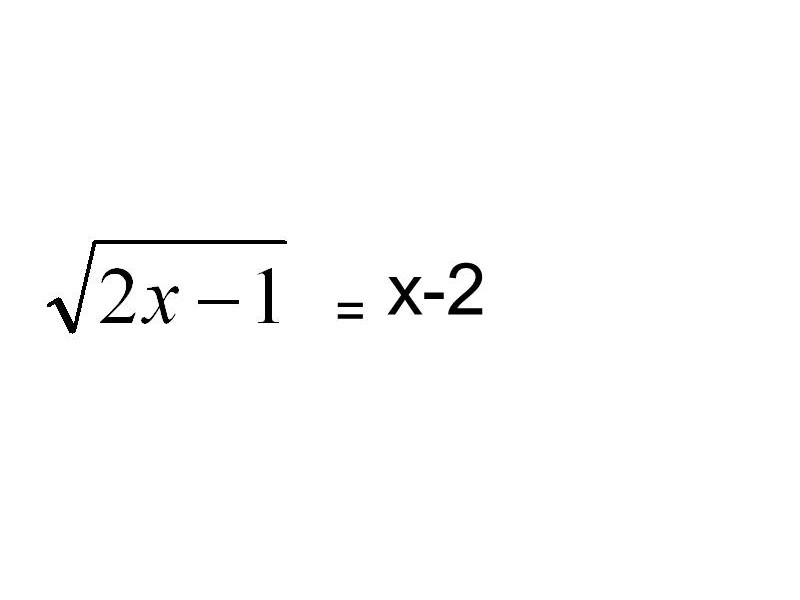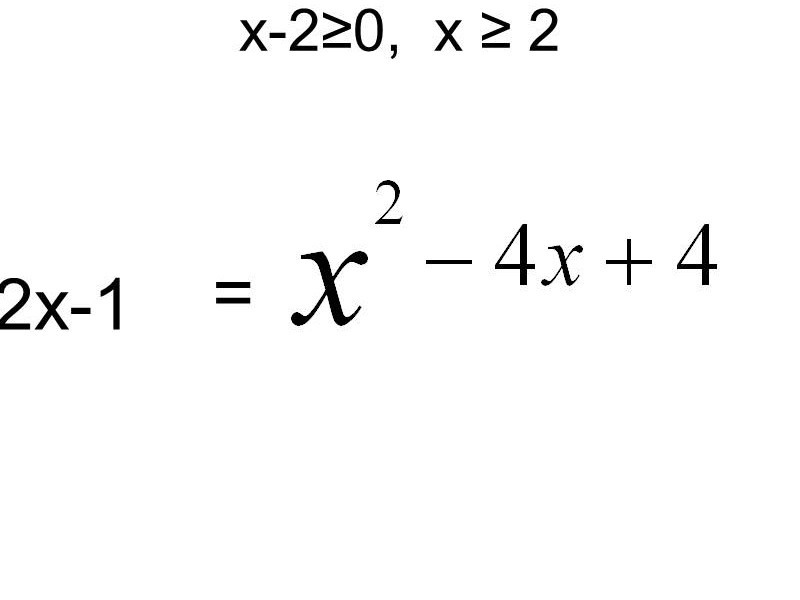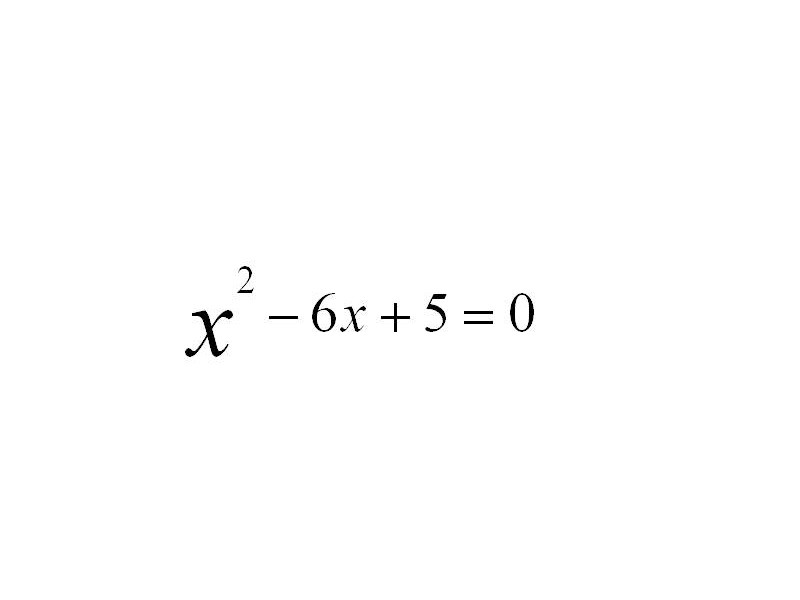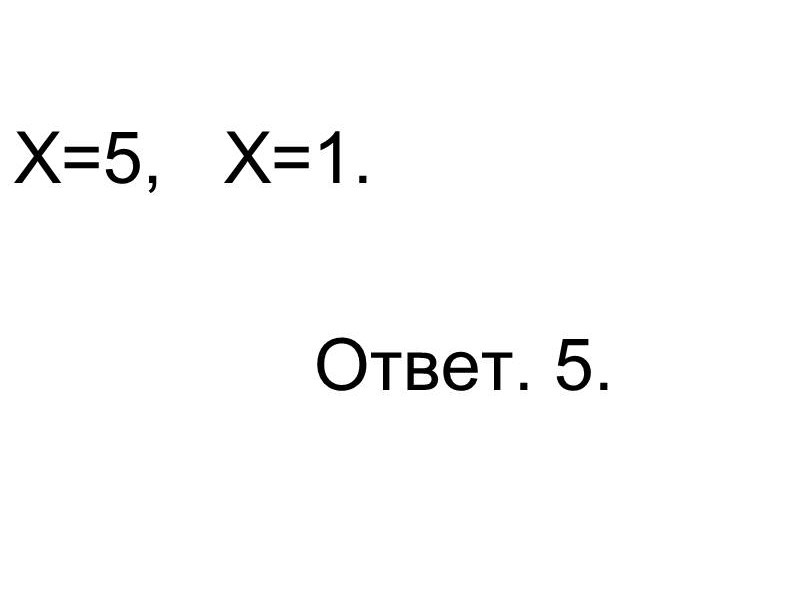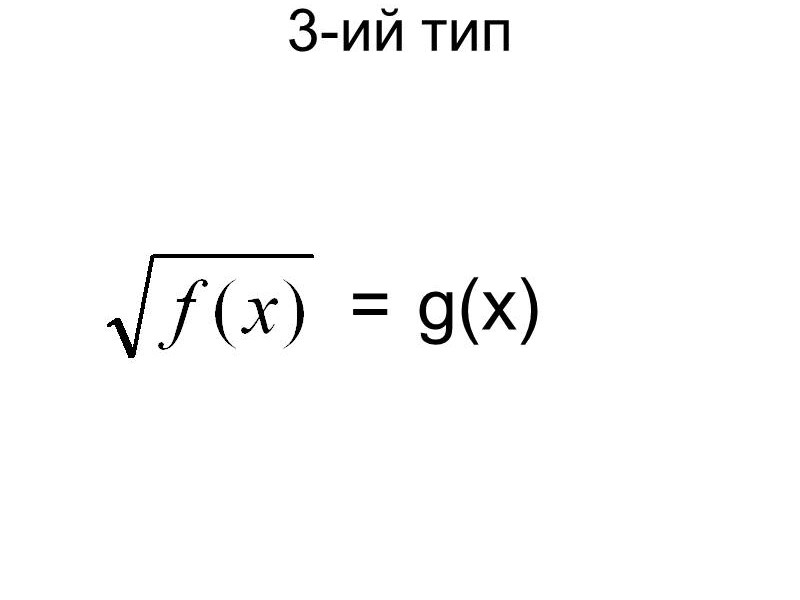Цели:
- повторить свойства степенной функции;
- повторить свойства арифметических корней;
- дать понятие иррационального уравнения;
- рассмотреть примеры решения иррациональных уравнений.
Оборудование урока:
- Интерактивный комплекс.
- Карточки для проведения самостоятельной работы.
ПЛАН УРОКА.
1. Проверка домашнего задания.
2. Устная работа.
а) сравнить m и n, если
б) четным или нечетным является показатель функции y= f (x), если: f(-5)> f(-3); f(-5)> f(3); f(-5)<f(-3); f(-5)< f(3); f(5)> f(-3); f(5)> f(3);
в) вычислить
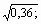
-
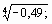
-
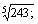
-
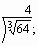
-
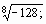
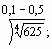
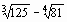 .
.
3. Изучение нового материала.
Уравнения, в котором под знаком корня
содержится переменная, называют
иррациональными. То есть ![]() =
=![]() или
или ![]() = g(x).
= g(x).
Как правило, иррациональное уравнение сводится к равносильной системе, содержащей уравнения и неравенства.
Рассмотрим решение различных типов уравнений.
1-й тип.
![]() =
=![]()
![]()
| {f(x)=g(x) f(x) |
или | {f(x)=g(x) g(x) |
Пример 1.
![]() =
= ![]()
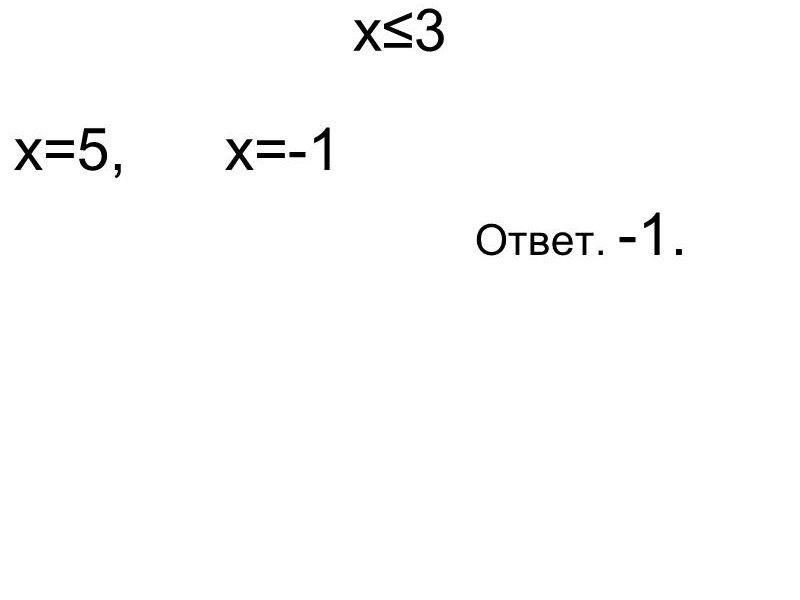
3-x= ![]() , 3-x
, 3-x ![]() 0
0
![]() x
x ![]() 3
3
x=5, x=-1
Ответ. -1.
2-й тип.
![]() =а
=а
Если a < 0, то уравнение корней не имеет.
Если a ![]() 0, уравнение
равносильно уравнению f(x)=a.
0, уравнение
равносильно уравнению f(x)=a.
Пример 2.
![]() = х-2
= х-2
2х-1 =![]() , х-2
, х-2 ![]() 0, х
0, х ![]() 2
2
![]()
D = 16 , ![]()
![]() = 5,
= 5, ![]() =1
=1
Ответ. 5.
3-й тип.
![]() = g(x)
= g(x) ![]() {f(x)=
{f(x)= ![]()
g(x) ![]() 0
0
Пример 3.
![]() = х – 1
= х – 1
7-х = ![]() , х-1
, х-1 ![]() 0, х
0, х ![]() 1.
1.
![]()
D = 25, ![]() = 3,
= 3, ![]() =-2
=-2
Ответ. 3.
4. Работа с учебником.
5. Решение задач.
№ 418(а), 419(а),
6. Самостоятельная работа с самопроверкой.
Вариант 1 Вариант 2 = х
= х
= х-1
= х+2
Ответы: 4; 5. 6. Ответы: 5. 0; 1.
7. Итог урока.
а) определение иррационального уравнения;
б) типы рациональных уравнений;
в) способы их решения.
Задание на дом.
П.33, № 418(б,г), 419 (б,г).
Литература.
- Алгебра и начала математического анализа. А.М. Колмогоров и др. Москва, Просвещение, 2013.
- Алгебра и начала математического анализа. Г.К. Муравин, О.В. Муравина. Москва, Дрофа, 2013.
- Математика. Наглядный справочник. Л.Э. Генденштейн, А.П. Ершова, А.С. Ершова.