В своей работе я часто провожу в VII-XI классах уроки-зачеты по геометрии. Это хороший способ проверить готовность учащихся к контрольной работе по изученной теме.
Задание к зачету я предлагаю в начале темы. В него входят теоретические вопросы и практическая часть, состоящая из задач двух уровней сложности. Все могут решать задачи по мере изучения темы, а учащиеся, проявляющие интерес к предмету, имеют возможность реализовать свои способности и самостоятельно разбирать материал в удобное для них время.
Я провожу зачеты в различной форме: индивидуально для каждого ученика класса или с помощью различных игровых технологий. За правильностью ответов я слежу вместе с классом. В случае затруднения или неправильного ответа каждый ученик или группа может дать ответ, дополнить или поправить отвечающего. Ответы оцениваются баллами. Группе, выполнившей свое задание раньше всех, я добавляю 1 балл.
Оценка знаний на зачете:
“3” - при выполнении задания обязательного уровня без ошибок.
“4” - выполнены задания обязательного уровня и на 4.
“5” - выполнены задания всех уровней.
После подведения итогов учащимся выставляются оценки.
Приведенный ниже урок-зачет проводится по теме “Равенство треугольников”.
Цели урока:
- проверить степень усвоения учащимися признаков равенства треугольников;
- проверить умение применять признаки равенства треугольник при решении задач;
- повысить интереса к уроку;
- способствовать воспитанию внимательного и ответственного отношения к учёбе
- развивать коммуникативные навыки в групповой работе, чувства сплочённости, коллективизма.
Оборудование и материалы: медиа проектор, экран, презентация к уроку, карточки с номерами для лотереи, набор задач на готовых чертежах, листы для индивидуального решения задач, листы учёта знаний.
Ход урока
Слайд 1. Презентация
I. Организационный момент.
Учитель поясняет учащимся, как будет проходить урок. Класс делится на шесть групп: в каждой группе выбирается координатор (это лучше выполнить до начала урока). На каждом столе приготовлен лист учёта знаний, в котором координатор напротив каждой фамилии ставят "1 балл ", если учащийся дал верный ответ. По итогам каждого конкурса подсчитываются "баллы" и ставятся в строке "всего".
Слайд 2. Лист учёта группы
| Ф.И.учащихся | I | II | III | IV | V | Итого | Оценка |
| Всего |
Слайд 3. Общий лист учёта (располагается на доске)
| I группа | II группа | III группа | IV группа | V группа | VI группа | |
| I | ||||||
| II | ||||||
| III | ||||||
| IV | ||||||
| V | ||||||
| Итого |
Ход игры
I. Разминка
а) Версия двоечника Слайд 4
б) Блиц-опрос Слайд 5
II. Математический бой.
Каждая команда по очереди задает по 1 вопросу командам соперников, если какая-то команда не может дать ответ на поставленный вопрос, право ответить переходит к другой команде.
Координаторы выставляют баллы участникам команд.
1. Какая фигура называется треугольником?
2. Что такое периметр треугольника?
3. Какие треугольники называются равными?
4. Что такое теорема и доказательство теоремы?
5. Объясните, какой отрезок называется перпендикуляром, проведённым из данной точки к данной прямой.
6. Какой отрезок называется медианой треугольника? Сколько медиан имеет треугольник?
7. Какой отрезок называется биссектрисой треугольника? Сколько биссектрис имеет треугольник?
8. Какой отрезок называется высотой треугольника? Сколько высот имеет треугольник?
9. Какой треугольник называется равнобедренным?
10. Как называются стороны равнобедренного треугольника?
11. Какой треугольник называется равносторонним?
12. Сформулируйте свойство углов при основании равнобедренного треугольника.
13. Сформулируйте теорему о биссектрисе равнобедренного треугольника, проведенную к основанию.
14. Сформулируйте первый признак равенства треугольников.
15. Сформулируйте второй признак равенства треугольников.
16. Сформулируйте третий признак равенства треугольников.
III. Задачи на готовых чертежах “Пришел, увидел и решил”. Слайд 6-10
Каждая команда выбирает номер задачи случайным образом (лотерея) и решает по 3 задачи. Решения представляются у доски.
IV. “Дальше, дальше…”
Каждая группа получает карточку с заданием отметить знаком “+” правильные утверждения, а знаком “-” - ошибочные.
Задание 1 и 4 группе
Задание 2 и 5 группе
Задание 3 и 6 группе
V. "Гонка за лидером"
Каждая группа получает карточки с индивидуальными задачами для каждого учащегося.
- Свои решения, выполненные на листках, учащиеся сдают учителю.
- Те учащиеся, которые решили свою задачу раньше других, получают дополнительные индивидуальное задание.
- Та команда, члены которой первыми справятся с решением всех задач получает дополнительно 1 балл.
Задачи.
1. На высоте АН равнобедренного треугольника АВС с углом А=900 взята точка О. Докажите, что ВОН и НОС равны.
2. AD и CE - биссектрисы равнобедренного треугольника с основанием AC. Докажите, что ACE = CDA.
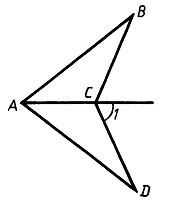
3. Точки С и D расположены по разные стороны от прямой АВ так, что AD = AC, BD = DC. Докажите, что AB – биссектриса угла DAC
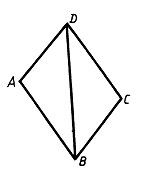
4. На рисунке АВ = CD, BC = AD, ![]() ABD = 27°. Найдите величину угла BDC.
ABD = 27°. Найдите величину угла BDC.
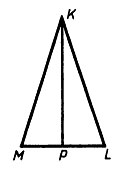
5. KP – биссектриса MKL, изображенного на рисунке. MK = KL. Найдите длину отрезка MP, если известно, что PL = 8 см.
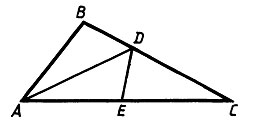
На рисунке BD = DE, ![]() BDA
=
BDA
= ![]() EDA. Докажите, что
AD - биссектриса треугольника ABC.
EDA. Докажите, что
AD - биссектриса треугольника ABC.
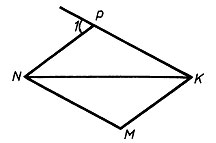
7. На рисунке NP = MK, MN = PK, ![]() NMK = 137°. Найдите
NMK = 137°. Найдите ![]() 1
1
8. На рисунке AB = AD, BC = CD, ![]() ACB = 121°. Найдите
ACB = 121°. Найдите ![]() 1.
1.
9. AE и KM – биссектрисы равнобедренного треугольника APK с основанием AK. Докажите, что треугольники APE и KPM равны.
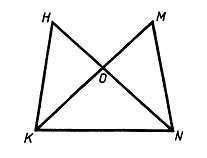
10. На рисунке ![]() HKN=
HKN=![]() MNK, KO = ON. Докажите,
MNK, KO = ON. Докажите, ![]() KHN =
KHN =![]() KMN.
KMN.
11. Точки М и Е расположены по разные стороны от
прямой ОР так, что ОМ = РЕ и МР = ОЕ. Докажите, что ![]() МОР =
МОР = ![]() ЕРО и
ЕРО и ![]() МРО=
МРО= ![]() ЕОР.
ЕОР.
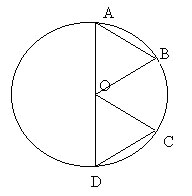
12. На рисунке хорды АВ и CD равны. Докажите, что ![]() AOB =
AOB =![]() COD.
COD.
Дополнительные задачи: Слайд 7.
III. Подведение итогов урока.
В итоге оценка за урок выставляется каждому учащемуся по листу учёта знаний. Члены той команды, которая больше всего набрала баллов за игру получают на 1 балл оценку выше, чем члены других команд.