На занятии изучается методика решения уравнений высших степеней. Рассматриваются два метода: разложение на множители и замена переменной. Понижение степени уравнений с помощью деления многочленов по схеме Горнера и приведение различных уравнений к замене переменной. Дана историческая справка исследования уравнений высших степеней. Представлена презентация урока.
Метод разложения на множители.
Этот метод основан на применении теоремы Безу. Если число α является корнем многочлена P(x) степени n, то его можно представить в виде P(x) = (x - α)Q(x), где Q(x) - многочлен степени (n-1).Теорема Безу: “Остаток от деления многочлена Р(х) на двучлен (x - α) равен P(α), т.е. значению многочлена при x = α” Таким образом, если известен хотя бы один корень уравнения Р(х)=0 степени n, то с помощью теоремы Безу можно свести задачу к решению уравнения степени (n-1), понизить степень уравнения. Теорема. Пусть несократимая дробь p/q является корнем уравнения a0xn + a1xn-1+ ... + ax-1x+ an = 0 с целыми коэффициентами, тогда число p – является делителем свободного члена an, а q – делителем старшего коэффициента a0. У многочлена с целыми коэффициентами целые корни являются делителями свободного члена. Таким образом, зная корень многочлена, его легко разложить на множители, т.е. разделить P(x) на (x - α) “углом” или по схеме Горнера.
Схема Горнера
|
a0 |
a1 |
a2 |
... |
an-1 |
an |
α |
a0 |
b1 = α a0 + a1 |
b2 = α b1 + a2 |
... |
bn-1 = α bn-2 + an-1 |
0 |
(x - x1)(x - x2) ... (a0x2 + bx + c) = 0, x1= α – корень многочлена.
Пример №1. x3 - 9x2 + 26x - 24 = 0 Решение. Выпишем делители свободного члена
p = ±1; ±2; ±3; ±4; ±6; ±8; ±12; ±24, R(2) = 0, x1= 2.
Понизим степень уравнения делением многочленов в столбик «углом»
x3 - 2x2
-7x2 + 26x
-7x2 + 14x
12x - 24
12x - 24
Разложим на множители (x - 2)(x2 - 7x + 12) = 0, x1 = 2, x2 = 3, x3 = 4.
Ответ: {2;3;4}
Решить самостоятельно.
Пример №2: x3 + 7x2 - 56x + 48 = 0 Ответ: {1;4;-12}
Пример №3: x3 - 5x2 - 2x + 16 = 0 Ответ: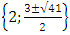 
Понижение степени по схеме Горнера.
Пример №4: x4 + 3x3 - 24x2 + 17x + 3 = 0
Решение. Найдем делители свободного члена p =±1; ±3, R(1) = 0, x1= 1.
|
1 |
3 |
-24 |
17 |
3 |
|
1 |
1 |
4 |
-20 |
-3 |
0 |
x1= 1 |
3 |
1 |
7 |
1 |
0 |
|
x2= 3 |
Разложим на множители (x - 1)(x - 3)(x2 + 7x + 1) = 0 Ответ: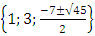 
Пример №5: x6 - x5 - 8x4 + 14x3 + x2 - 13x + 6 = 0
p = ±1; ±2; ±3; ±6
|
1 |
-1 |
-8 |
14 |
1 |
-13 |
6 |
|
1 |
1 |
0 |
-8 |
6 |
7 |
-6 |
0 |
x1= 1 |
-1 |
1 |
-1 |
-7 |
13 |
-6 |
0 |
|
x2= -1 |
2 |
1 |
1 |
-5 |
3 |
0 |
|
|
x2= 2 |
-3 |
1 |
-2 |
1 |
0 |
|
|
|
x2= -3 |
Разложим на множители (x - 1)(x + 1)(x - 2)(x + 3)(x2 - 2x + 1) = 0
(x - 1)(x + 1)(x - 2)(x + 3)(x - 1)3 = 0
Ответ: {±1; 2; -3}
Пример №6: 2х4– 7х3 – 3х2 + 5х – 1 = 0, p = ± 1,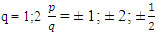 
|
2 |
-7 |
-3 |
5 |
-1 |
|
1 |
2 |
-5 |
-8 |
-3 |
-4 |
не корень |
-1 |
2 |
-9 |
6 |
-1 |
0 |
x1= -1 |
0,5 |
2 |
-8 |
2 |
0 |
|
x2= 0,5 |
(х + 1)(х – 0,5)(2х2 – 8х + 2) = 0
х2 – 4х + 1 = 0 D/4 = 4 – 1 = 3 x = 2 ±√3 Ответ: {1; 0,5; 2 ±√3}
Решить самостоятельно.
Пример №7: 2х4 + 17х3 – 17х2 - 8х + 6 = 0 Ответ: {1/2; 1; -5 ±√19}
Пример №8: х4 + 3х3 – 5х2 - 13х + 6 = 0 Ответ: {2; -3; -1 ±√2}
Замена переменной.
Пример №9:
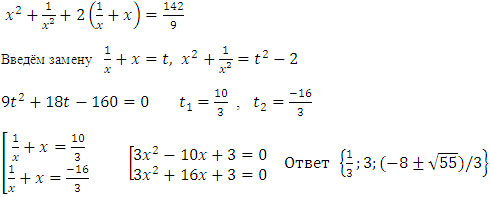
1. Возвратные уравнения
a0xn + a1xn-1+ ... + an-1x+ an = 0 – Возвратное симметричное, если a0 = an, a1 = an-1 и т.д.
1) Для нечетных возвратных многочленов справедлива теорема: “Всякий возвратный многочлен нечетной степени имеет корнем х = -1. Затем схема Горнера.
2) Возвратное уравнение 4-й степени aх4 + bх3 + cх2 + bx + a = 0, a ≠ 0. Делим на x2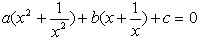 
Получим замену
 |
 |
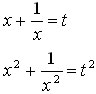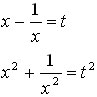Пример №10: 6х4 - 35х3 + 62х2 - 35x + 6 = 0
Делим на x2, получим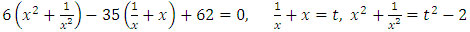 
6t2 - 35t + 50 = 0 t1= 5/2; t2= 10/3
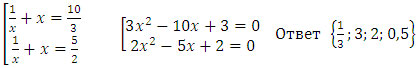
Решить самостоятельно.
Пример №11: 2х4 + 3х3 - 24х2 - 3x + 2 = 0 Ответ: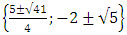 
Пример №12: 12х4 - 16х3 - 11х2 - 16x + 12 = 0 Ответ: {2; 0,5}
2. Однородные уравнения.
a0xn + a1xn-1y + ... + ax-1xyn-1+ anyn = 0 Делим на yn, x ≠ 0, y ≠ 0.
a0(x/y)n + a1(x/y)n-1 + ... + an-1(x/y)+ an = 0, получим замену x/y = t
a0tn + a1tn-1 + ... + an-1t+ an = 0
Пример №13: 2х4 + х2(x + 2) - 3(x + 2)2 = 0 Делим на (x + 2)2, получим
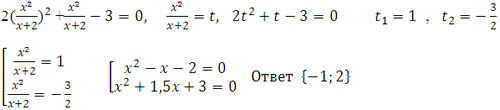
Решить самостоятельно.
Пример №14: (x - 1)4 + 9(x + 1)4 = 10(x2 - 1)2 Ответ: {-2; -0,5; 0}
3. Уравнения (x + a)(x + b)(x + c)(x + d) = m, m ≠ 0.
Если выполняется одно из условий a + b = c + d, b + c = a + d, a + c = b + d, то выполняется замена переменной.
Пример №15: (x + 2)(x - 3)(x + 1)(x + 6) = -96; 2+1=-3+6
(x + 2)(x - 3)(x + 1)(x + 6) = -96, (x2 + 3x + 2)(x2 + 3x - 18) = -96
x2 + 3x = t, (t + 2)(t - 18) = -96, t2 - 16t + 60 = 0, t1=10, t2=6
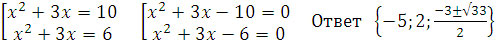
Решить самостоятельно.
Пример №16: (x - 2)(x + 4)(x + 1)(x + 7) = 63
4. Уравнения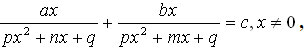 
приводим к замене
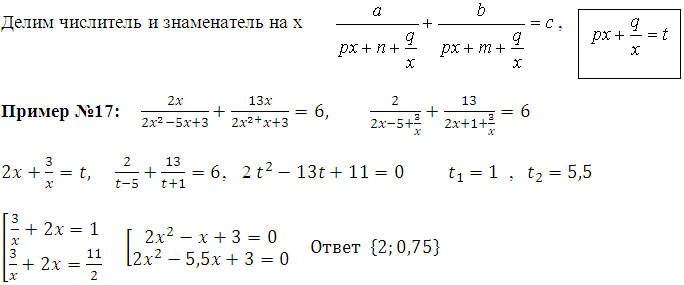
Решить самостоятельно.
Пример №18: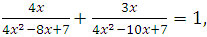 
Ответ: {0,5; 3,5}
5. Биномиальные уравнения
(x + a)n + (x + b)n = c, замена x = t - (a + b)/2, получим (t - p)n + (t + p)n = c. Применяем формулу бинома Ньютона
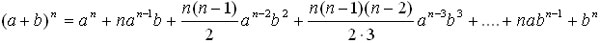
Пример №19: (x + 6)4 + (x + 4)4 = 82, x = t - (6+4)/2 = t-5,
(t - 1)4 + (t + 1)4 = 82, t 4 + 4t3 + 6t2 + 4t + 1+ t4 - 4t3 + 6t2 - 4t + 1 = 82,
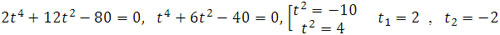
x1= -3, x2= -7. Ответ: {-3; -7}
Решить самостоятельно.
Пример №20: (x + 3)4 + (x + 5)4 = 16, Ответ: {3; -5}
Домашнее задание:
Пример №2: x3 + 7x2- 56x + 48 = 0 Ответ: {1; 4; -12}
Пример №3: x3 - 5x2- 2x + 16 = 0 Ответ: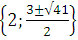 
Пример №7: 2x4 + 17x3 - 17x2- 8x + 6 = 0 Ответ: {1/2; 1; -5 ±√19}
Пример №8: x4 + 3x3 - 5x2- 13x + 6 = 0 Ответ: {2; -3; -1 ±√2}
Пример №11: 2x4 + 3x3 - 24x2- 38x + 2 = 0 Ответ: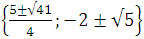 
Пример №12: 12x4 - 16x3 - 11x2- 16x + 12 = 0 Ответ: {2; 0,5}
Пример №14: (x - 1)4 + 9(x + 1)4 = 10(x2- 1)2 Ответ: {-2; -0,5; 0}
Пример №16: (x - 2)(x + 4)(x + 1)(x + 7) = 63
Пример №18: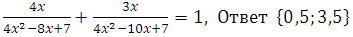 
Пример №20: (x + 3)4 + (x + 5)4 = 16, Ответ: {3; -5}
Историческая справка
Квадратные уравнения
1.1. Индийский ученый Брахмагупта (VIIв) – правило решений квадратных уравнений.
1.2. После трудов Нидерландского математика А.Жирара (1595-1632г.), а также Декарта и Ньютона способ решений квадратных уравнений принял современный вид.
1.3. Ф. Виетт (1591г.) – зависимость корней от коэффициента.
Кубические уравнения х3+рх +q = 0
1.4. Сципион Даль Ферро (1465-1526г.) и его ученик Фиори.
1.5. Н. Тарталья (1499-1557г.) – не опубликовал своих трудов.
1.6. Д. Кардано (1501-1576г.), «Великое искусство, или о правилах алгебры» – узнал об открытии Тартальи.
Формула корней кубического уравнения (формула Кардано)
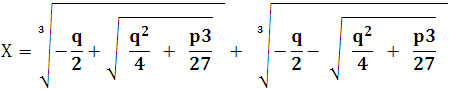
х3+х - 1 = 0
р=1 q= -1
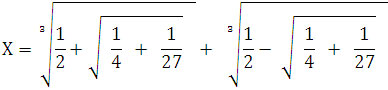
Уравнения 3-й и 4-й степени
1.7. Ученик Кардано Л.Феррари (1522-1567г.) – метод решения уравнения 4й степени.
1.8. Р.Бомбелли (1530-1572г.) – полное исследование кубических уравнений.
1.9. Ф.Виет (1540-1603г.) – полное изложение вопросов, связанных с решением уравнений 3й и 4й степени.
Уравнения 5-й степени
1.10. Норвежский математик Н. Абель (1802-1829г.) – доказал, что в общем случае корни уравнений 5й степени и более высоких степеней не могут быть выражены через радикалы.
1.11. Французский математик Э. Галуа (1811-1832г.) выделил класс алгебраических уравнений, которые разрешены в радикалах.