Предварительная подготовка к уроку:
Учащиеся должны знать признаки равенства произвольных треугольников, понятие прямоугольного треугольника, гипотенузы и катетов. На предшествующем уроке ученики изучили только один признак равенства прямоугольных треугольников (по гипотенузе и катету) и доказали его.
Цели урока:
- доказать признаки равенства прямоугольных треугольников, уметь применять их при решении задач, повторить признаки равенства произвольных треугольников;
- развивать логическое мышление, внимание, навыки исследовательской работы, навыки аргументированной речи;
- воспитать познавательную активность, чувства ответственности и взаимовыручки, повышать интерес к изучению математики, показать возможность применения математических знаний в жизни;
- формировать у учащихся навыки работы в группах.
Методы и приемы: наглядный метод, словесный метод, постановка проблемных вопросов, поисковый метод, дифференцированный подход.
Формы работы: коллективная, индивидуальная, устная и письменная.
Оборудование: компьютер, проектор, угольники, 3 листа бумаги А3 с заданиями, индивидуальные карточки, презентация (Приложение 1)
Тип урока: комбинированный
ХОД УРОКА
1. Ориентировочно-мотивационный этап
Организационный момент
Учитель: Дорогие ребята, вы уже знаете признаки равенства треугольников. Сколько пар равных элементов надо найти у треугольников, чтобы воспользоваться одним из признаков равенства треугольников? Поясните ответ.
Ответ: 3. (по 3 признаку – 3 пары соответствующих сторон, по 1 признаку – 2 пары соответствующих сторон и пара углов между ними или по 2 признаку – пара сторон и 2 пары прилежащих углов.)
Учитель: А какие равные элементы есть всегда у любых прямоугольных треугольников?
Ответ: Это прямой угол.
Учитель: Как вы думаете, сколько пар равных элементов будем искать для доказательства равенства прямоугольных треугольников?
Ответ: 2.
Учитель: Да, на прошлом уроке был доказан признак по гипотенузе и катету. Сегодня рассмотрим все остальные признаки для прямоугольных треугольников.
2. Актуализация знаний (фронтальная работа)
Учитель: На слайде презентации записан пока один признак (по гипотенузе и катету). Запишем его название в тетрадь: «1. По гипотенузе и катету». Примените признак равенства по двум сторонам и углу между ними к прямоугольным треугольникам и сформулируйте признак для прямоугольных треугольников.
Ответ: По двум катетам: Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны.
Учитель: на слайде появился и этот признак. Записываем его в тетрадь: «2. По двум катетам». Сформулируйте признак, в котором использовалась бы гипотенуза.
Ответ: По гипотенузе и острому углу. Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.
Учитель: Запишем его название в тетрадь: «3.По гипотенузе и острому углу». Какой признак равенства треугольников используется для доказательства признака «по гипотенузе и острому углу»?
Ответ: По стороне и прилежащим к ней углам.
Учитель: Вы, наверное, догадались, что следующий признак «по катету и острому углу».
Прежде чем его сформулировать и записать, предлагаю вам проанализировать рисунок на слайде:

Учащиеся должны заметить, что треугольники на слайде не являются равными, хотя они имеют равные катеты и равные острые углы (как вертикальные).
Ребятам предлагается для анализа и следующий рисунок на слайде:
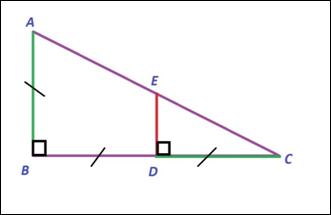
Учитель: Какой признак с катетом и углом будет правильным?
Ответ: По катету и прилежащему острому углу или по катету и противолежащему острому углу.
Учитель: Записываем в тетрадь 4 и 5 признаки.
3. Первичное закрепление знаний (устная работа)
Учитель: Назовите цвета пар равных прямоугольных треугольников, изображенных на следующем слайде, и определите, по какому признаку они равны:

Ответ: Светло-зеленые треугольники – по двум катетам, темно-зеленые – по катету и противолежащему острому углу, красные – по гипотенузе и острому углу, синие – по двум катетам, розовые – по катету и прилежащему острому углу.
4. Решение задач
Задача №1 (условие на слайде презентации):

Учитель дает время на устное решение задачи, а потом один ученик объясняет решение у доски.
В ходе решения в презентации появляется следующий чертеж на слайде:
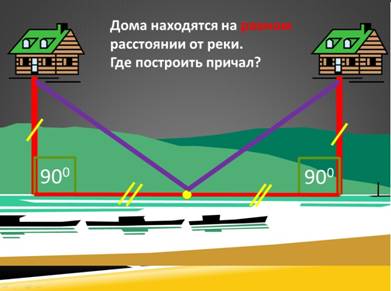
Решение: Опускаем перпендикуляры к прямой, они равны, так как равны расстояния до реки. Причал будет в середине отрезка, соединяющего основания перпендикуляров. Получаем равные перпендикулярные треугольники по двум катетам. Значит, расстояния от причала до домов равны, как равные гипотенузы.
Задача №2 (условие на слайде презентации):
Точки В и D лежат в разных полуплоскостях относительно прямой АС.
AB = CD, AB || CD, BM ![]() AC, DK
AC, DK ![]() AC.
AC.
Докажите, что BM = DK.
Ученик делает чертеж на доске и решает задачу, записывает решение на доске, а остальные учащиеся в тетрадь.
При решении нужно рассмотреть и следующий случай:
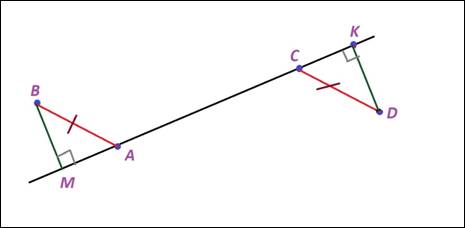
<ВАС=<АСD как внутренние накрест лежащие при параллельных прямых AB и CD с секущей АС.
<ВАМ=<КСD как смежные с равными углами
∆ВМА= ∆ DКС (прямоугольные по гипотенузе и острому углу), ВМ=DК
5. Гимнастика для глаз (в презентации слайд №9)
6. Самостоятельная работа
Задание на слайде презентации:
Используя угольник, выполните дополнительные построения на чертежах так, чтобы получить равные прямоугольные треугольники. Докажите их равенство.
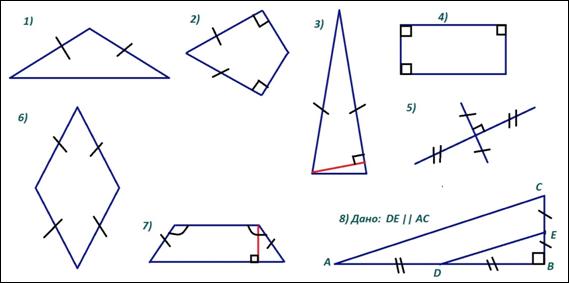
Учащиеся получают карточки с этим заданием и выполняют его в парах.
На доске помещаются 3 плаката с этим заданием на обратных сторонах крыльев доски. После отведенного времени на все задание (12 минут) по очереди по 1 человеку от ряда (команды) выходит ученик и выполняет построения к 1 чертежу на плакате, потом выходит следующий и делает построения ко 2 чертежу и т.д. Выигрывает тот ряд (команда), который раньше остальных выполнит построения ко всем 8 чертежам. Плакаты друг друга с выполненными построениями учащимся не видно. Затем демонстрируются все плакаты и слайд на презентации с возможными построениями:
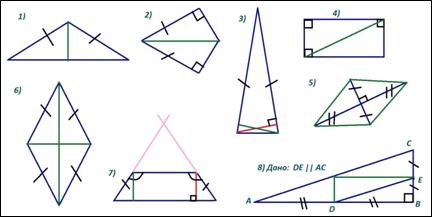
После этого учитель приглашает к доске одного ученика для объяснения построения и доказательства равенства треугольников в задачах 1-2, потом одного для задач 3-4, следующего для задач 5-6, для 7 и 8 задач по одному ученику, учитывая, что задачи расположены в порядке возрастания сложности. (Ученики используют плакаты).
Решение:
 1) Проводим высоту к основанию. Треугольники равны, например, по гипотенузе и катету.
1) Проводим высоту к основанию. Треугольники равны, например, по гипотенузе и катету.
2) Гипотенуза – общая. Треугольники равны по гипотенузе и катету.
3) Проводим высоту к боковой стороне равнобедренного треугольника. Угол между боковыми сторонами треугольника – общий. Треугольники равны по гипотенузе и острому углу.
4) Треугольники, например, равны по двум катетам или по катету и гипотенузе.
5) Треугольники равны по двум катетам.
6) ∆DAB и ∆DCB – равнобедренные, <1= <2, <3=<4 как углы при основании равнобедренного треугольника
∆DAB = ∆DCB (по трем сторонам), значит,
<1= <2=<3=<4
∆CDA и ∆CBA равнобедренные, DO и BO – биссектрисы, проведенные к основанию,
значит, DO и BO – высоты
∆DAО и ∆BАО, ∆DСО и ∆BCО прямоугольные, <О=900
Они равны по гипотенузе и острому углу.
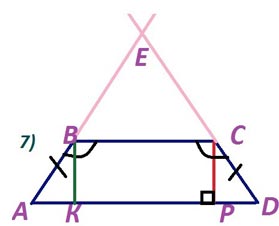
7) <EBC = <ECB как углы, смежные с равными.
Значит, ∆ EBC – равнобедренный по признаку равнобедренного треугольника.
Следовательно, ЕВ = ЕС, ЕА = ЕD
∆ EAD равнобедренный, значит углы при его основании <A = < D.
Из точки В опускаем перпендикуляр ВК на АD, получаем прямоугольные треугольники АВК и DСР, равные по гипотенузе (АВ = СD) и острому углу (<A = < D).
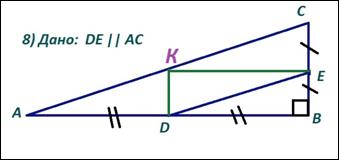
8) Проведем КЕ ![]() СВ, <КСЕ = <DЕВ как соответственные углы при параллельных прямых DE и АС и секущей СВ
СВ, <КСЕ = <DЕВ как соответственные углы при параллельных прямых DE и АС и секущей СВ
∆КСЕ =∆DEB по катету и прилежащему острому углу.
Доказательство равенства с остальными прямоугольными треугольниками – это будет домашнее задание.
7. Подведение итогов
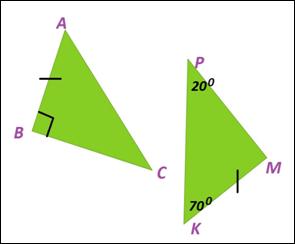
Задание на слайде презентации: Можно ли утверждать, что данные треугольники равны?
Ответ: Нет.
Учитель: Каких равных элементов не хватает для доказательства равенства этих треугольников?
Ответ: Или равенства гипотенуз, или катетов, или равенства острых углов.
Ученик перечисляет признаки равенства прямоугольных треугольников.
8. Домашнее задание (№8 из карточки)