Цели урока:
-
ввести понятие критических точек функции, точек экстремума;
-
доказать необходимое условие экстремума;
-
способствовать выработке навыка отыскания экстремумов
-
функции, развитию логического мышления учащихся.
Оборудование: учебник “Алгебра и начала анализа под ред. А.Н. Колмогорова, дидактические материалы для 10-11 классов, таблицы.
Ход урока
I. Оргмомент.
II. Сообщение темы, целей, задач урока.
III. Изучение нового материала.
1. С помощью графика ответить на следующие вопросы:
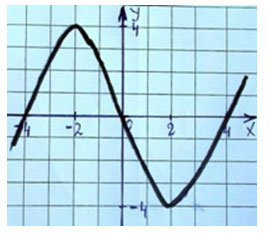
2. Назвать нули функции (х = -4, х = 0, х = 4);
промежутки знакопостоянства ((-4;0) и (4; +∞) – f (х) > 0); (-∞,-4) и (0;4) - f (х)<0).
3. Промежутки монотонности ((-∞ ;-2] и [2; +∞) – функция возрастает, [-2; 2] – функция убывает)
4. Точки максимума и минимума (х = -2 –точка максимума, f (-2) = 4; х = 2 – точка минимума, f (2) = - 4)
.5. Множество значений функции: (-∞, +∞)
Остановимся подробнее на точках экстремума. Вспомним определение точек максимума и минимума.
По рисункам назвать точки максимума и минимума
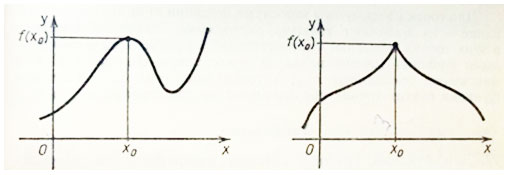
Вопрос. Что можно сказать о наличии производной в этих точках и об ее значении?
Гипотеза: в точках экстремума производная равна 0.
Теорема Ферма
Если точка х0 является точкой экстремума функции и в этой точке существует производная f , то она равна нулю, f (х0 ) = 0.
(Доказательство самостоятельно).
Определение критических точек.
Теорема Ферма: х0 – точка экстремума => х0 – критическая точка.
Верно ли обратное утверждение.
Рассмотрим функцию f (х) = х3, f (х) = 3х2, х = 0 – критическая точка, х0 – критическая точка, но не является точкой экстремума.
Вывод: теорема Ферма является лишь необходимым условием для того, чтобы х0 была точкой экстремума для функции f, она дает основание “отобрать” точки, “подозрительные” на экстремум. Утверждать, что в этих точках функция действительно имеет экстремум, нельзя, нужна дополнительная проверка. Какая? Это мы выясним несколько позже.
IV. Закрепление новой темы.
1. Найти критические точки функции:
F(x)=42-x+7x2 G(x)=1+cos x, Q(x)= x-2 sin x
2. Доказать что функция не имеет критических точек
Y= tgx Y=3x-7
3. Работа в парах (карточки)
Найдите максимум и минимум функции:
f(x)= x ³ - 4x ² +5x-1
f(x)= x ³ - 4x ² +7x+2
4. “Найди ошибку”.
f (х) = ![]()
Д (f ) = [0; +∞)
f (х) = ![]()
f (х) = 0 при х = 1
f (х) не существует при х = 0, х = -1
х = 1 – критическая точка
х = 0 – критическая точка
х = -1 – критическая точка
V. Информация о домашнем задании.
П. 23; № 290, 291.
Самоанализ урока
в 10 классе по теме “Критические точки функции”
Урок по данной теме занимает место в системе уроков в разделе “Производная и ее применение”.
Тип урока: изучение нового материала.
При планировании учтены реальные учебные возможности учащихся 10 класса.
Урок связан с предыдущими (используются понятия нулей функции, промежутков знакопостоянства, точек максимума и минимума) и изученный материал является необходимым для доказательства необходимым для доказательства достаточного условия экстремума функции.
В ходе проведения занятия осуществлялось единство обучающей, развивающей и воспитывающей функций урока.
Выбранная структура урока соответствует содержанию учебного материала, логично осуществлялся переход от одного этапа к другому. Выделялись главные, существенные, важные понятия: (определение критических точек функции, “чтение графиков”, рассматривалось доказательство теоремы Ферма).
При изучении нового материала ставились проблемы перед учащимися, помогающие активизировать учебно-познавательную деятельность.
С целью контроля знаний учащихся использовались различные методы: устный опрос, карточки индивидуальных заданий с заданиями различного уровня сложности.
Обращалось внимание на развитие познавательных интересов; перед доказательством теоремы Ферма перед учащимися был поставлен проблемный вопрос о значении производной в критической точке функции.
Задание “Найди ошибку” позволяет активизировать мыслительную деятельность, способствует анализу, синтезу, обобщению.
Урок по данной теме достиг поставленных целей, носил обучающий характер, методы обучения соответствовали выбранному типу урока.