Цель урока: Сформировать и доказать теорему о площади круга, вывести формулы нахождения площадей круговых сектора и сегмента, научиться применять их при решении задач.
Учебная задача: научить учащихся использовать формулы площади круга, кругового сектора и сегмента при решении практических задач;
Развивающая задача: использовать исследовательскую деятельность, развивать интуицию, стремление к применению полученных знаний.
Воспитательная задача: формирование навыков поиска рациональных путей решения задач, воспитывать уважение к значимости полученных знаний
Урок 1
План урока.
I этап. Повторение теоретического материала по теме “Площадь многоугольника” (слайд 2)
II этап. Объяснение нового материала (Слайд 3,4);
III этап. Решение практических задач (5 - 9 слайды).
ХОД УРОКА
I. Организационный момент
Сообщить тему урока, сформулировать цели урока.
II. Устная работа (повторение темы “Площадь многоугольника”) (слайд 2)
Какой многоугольник называется описанным около окружности?
Как найти площадь произвольного многоугольника?
Какой многоугольник называется правильным?
Формула площади правильного п-угольника, описанного около окружности.
Формула площади правильного п-угольника, вписанного в окружность.
III. Объяснение нового материала.
Изобразим окружность, назовем ее радиус R. Впишем в эту окружность правильные треугольник, четырехугольник, шестиугольник. (Слайд 3)
Вопросы
- Как определить длину данной окружности?
- Как определить периметры вписанных в нее правильных многоугольников?
- Сравним длину окружности (С = 2
 R) и периметры вписанных правильных
многоугольников (соответственно
R) и периметры вписанных правильных
многоугольников (соответственно 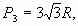
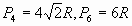 .
Видим, что длина окружности больше периметров
вписанных правильных многоугольников, причем С
> Рв> Р4> Р3.
.
Видим, что длина окружности больше периметров
вписанных правильных многоугольников, причем С
> Рв> Р4> Р3.
Вопрос
- Если продолжить увеличивать число сторон
правильного многоугольника, то как будут связаны
между собой С,
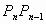 ?
Сделайте вывод.
?
Сделайте вывод.
Вывод. При увеличении числа сторон многоугольники приближаются к окружности. Поэтому площадью круга считают число, к которому приближаются площади вписанных правильных многоугольников при увеличении числа их сторон.
Теорема.(Слайд 4) Площадь круга равна половине произведения длины его окружности на радиус.
Рассмотрим правильный многоугольник, вписанный в данную окружность. Площадь этого правильного многоугольника равна половине произведения его периметра на радиус r вписанной в него окружности. При увеличении числа сторон многоугольников их периметры стремятся к длине окружности, а радиусы r вписанных окружностей стремятся к радиусу R исходной окружности. Поэтому площадь круга равна половине произведения длины окружности на радиус круга.
Таким образом, площадь S круга радиуса R
вычисляется по формуле S = ![]() R2.
R2.
III. Закрепление нового материала. (Слайды 5 – 9)
- Выведите формулу для нахождения площади круга
через его диаметр (D) (ответ
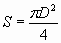 ) (Слайд 5).
) (Слайд 5). - Вычислите площадь круга, диаметр которого равен 4 см; (ответ 4?).
- Дайте определение фигуре, которая называется круговым сектором, или просто сектором.(Слайд 6)
- Вычислите радиус круга, площадь которого равна: 32 м2. (Слайд 7)
- Найдите площадь сектора, 1 если его центральный
угол равен: 1 а) 60°; б) 90°; в) 180°; г) 1°; д)
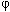 , а радиус соответствующего круга
равен R. (Слайд 7)
, а радиус соответствующего круга
равен R. (Слайд 7) - Выведите формулу нахождения площади кругового
кольца, заключенного между двумя
концентрическими окружностями с радиусами r и
R.(ответ
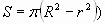 (Слайд
8)
(Слайд
8) - Из точки, принадлежащей кругу, радиус которого
равен г, проведены две равные и перпендикулярные
друг другу хорды. Найдите площадь части круга,
заключенной между этими хордами.(Слайд 9)(Ответ:
Искомая часть круга состоит из полукруга и
равнобедренного прямоугольного треугольника,
гипотенуза которого равна диаметру данного
круга, таким образом, искомая площадь равна
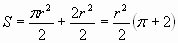 )
)
IV. Задание на дом
Выучить теорию (п. 62 учебника до площади сегмента), №4, 5, 9
Урок 2
План урока.
I этап. Проверка домашнего задания
II этап. Объяснение нового материала.
III этап. Актуализация знаний.
ХОД УРОКА
1. Организационный момент.
Сообщить тему урока, сформулировать цели урока.
2. Проверка домашнего задания (Слайд 10)
За первые парты приглашаются шесть учеников — опрос по теории.
3. Задание 1, 3, 5
Определение круга.
Теорема о площади круга.
Задание 2, 4, 6
Определение сектора.
Вывод формулы нахождения площади сектора.
Индивидуальные задания для учащихся по карточкам (выполняются на местах).
4. Задание для класса (Слайд 11)
1. Найдите площадь круга, длина окружности
которого равна: а) 2 см; б) 2![]() см. (Ответ: а)
см. (Ответ: а) ![]() см2.)
см2.)
2. Определение окружности.
3. Определение площади круга, диаметр которого равен D.
II. Новый материал (Слайд 12)
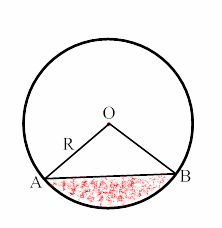
Рис.1
Определим фигуру, изображенную на рисунке 1. Круговым сегментом, или просто сегментом, называется часть круга, отсекаемая от него какой-нибудь хордой. Теперь найдем площадь сегмента.
Вопросы
- Из каких фигур состоит сегмент?
- Как можно вычислить площадь сегмента?
Площадь сегмента, ограниченного хордой АВ (рис.
1), можно найти как разность площади сектора АОВ и
площади треугольника АОВ. Пусть центральный угол
равен ![]() ,
радиус круга R. Тогда площадь сектора равна
,
радиус круга R. Тогда площадь сектора равна ![]() Поэтому
площадь сегмента будет выражаться формулой
Поэтому
площадь сегмента будет выражаться формулой ![]()
III. Актуализация знаний. (Слайды 13-16)
Найдите площадь сегмента, если радиус круга
равен R, дуга содержит(Слайд 13) а) 60°; б) 90°; в) 180°.
(ответ: ![]() ,
, ![]() ; в)
; в) ![]() )
)
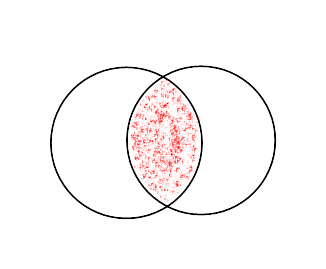
Рис. 2
Найдите площадь сегмента, если его хорда равна
а, а дуга содержит: а) 90°; б) 120°.(Слайд 14) (Ответ:
а) ![]() ; б)
; б) ![]() )
)
Найдите площадь заштрихованной фигуры на рисунке 2, а. Радиусы окружностей равны 1.
У ломаной ABCDE все вершины принадлежат окружности рис. 3) Углы вершинах В, С и D равны по 45°. Докажите, что площадь заштрихованной части круга равна половине его площади.
Решение: Дуги АС, СЕ и BD равны 90° (рис 44, б). Значит, дуги АВ и DE равны 45°. Следовательно, радиус ВО параллелен Рис. 2 АС, и поэтому треугольник ABC равновелик треугольнику АОС. Аналогично треугольник CDE равновелик треугольнику СОЕ. Таким образом, закрашенная фигура равновелика полукругу с диаметром АЕ и дугой АСЕ.
Итог урока. (Слайд 17)
IV. Домашнее задание:
Выучить теорию (п. 62 учебника) № 11, 13, 14
Литература:
- Геометрия 7 – 9 классы. Учебник. И.М.Смирнова, В.А.Смирнов. – М.: Мнемозина 2009
- Геометрия 9 класс. Рабочая тетрадь. И.М.Смирнова, В.А.Смирнов – М.: Мнемозина 2009
- Методические рекомендации для учителя 9 класс. И.М.Смирнова, В.А.Смирнов – М.: Мнемозина;. 2011