Цели урока:
- образовательная – воспроизведение и коррекция опорных знаний по теме; формирование навыков решения экзаменационных задач на геометрическую прогрессию;
- развивающая - развитие логического мышления, навыков самоконтроля в подготовке к ГИА;
- воспитательная – воспитание культуры умственного труда, познавательного интереса к предмету; коммуникативности.
Тип урока: урок обобщения и систематизации знаний.
Оборудование: комплекты для устного счета, раздаточный дидактический материал – тесты, сборники экзаменационных заданий, компьютер, видеопроектор, листки самоконтроля.
Структура урока:
| № | Этап урока | Вид работы | Содержание (цель) этапа | Время (мин) |
| I | Оргмомент. | Фронтально. | Постановка цели урока. Знакомство с планом работы на уроке. |
1 |
| II | Устный счет. | Фронтально, в парах. | Отработка устных вычислительных навыков. | 3 |
| III | Диктант по формулам. | Взаимопроверка. | Проверка и коррекция знаний формул геометрической прогрессии. | 5 |
| IV | Работа с тестом. | Работа в парах. Самопроверка. |
Формирование умений применять формулы
для установления истинности или ложности
утверждений. Развитие навыков самоконтроля. |
7 |
| V | Решение задач из сборника экзаменационных заданий. | Работа в группах. Проверка и коррекция решения через видеопроектор. |
Совершенствование навыков решения
задач на геометрическую прогрессию. Воспитание коммуникативности. |
15 |
| VI | Решение познавательных задач. | Построение графика. | Развитие навыков применения знаний по теме для решения познавательных задач. | 6 |
| VII | Задание на дом. | Запись в дневниках, чтение задания по учебнику. | Комментирование содержания домашнего задания. | 1 |
| VIII | Итог урока. | Проверка листов самоконтроля. | Обобщение полученных результатов работы через листы самоконтроля. Предварительное выявление проблем. | 2 |
Ход урока
I. Оргмомент.
Объявить тему урока, дидактическую цель, сообщить план работы.
II. Устный счет.
Раздаточный материал для устного счета находится на столах учащихся. Каждый сидящий на 1 варианте отвечает по одному примеру, сосед по парте проверяет ответ.
Задания для устного счета.
Вычислите:
1) 53; 2) 24; 3) (-2)7; 4) (0,2)2; 5) (-0,2)3; 6) (-1)2; 7) (-1)5; 8) (-0,3)2; 9) 1,32; 10) 160;
![]()
![]()
![]()
![]()
![]()
16) 210 : 28; 17) 32 : 3; 18) 32n + 2 : 32n; 19) 24 * 23; 20) 0,5 * 23.
III. Диктант по формулам.
Класс пишет под диктовку учителя, один учащийся работает на обороте доски. Затем ответы открываются, учащиеся за партой меняются тетрадями, и проводится взаимопроверка.
Задание 1. Запишите рекуррентную формулу n-го члена геометрической прогрессии и выразите из нее знаменатель прогрессии.
Задание 2. Запишите формулу n-го члена геометрической прогрессии.
Задание 3. Запишите формулу суммы n первых членов геометрической прогрессии.
Задание 4. Запишите формулу суммы бесконечно убывающей геометрической прогрессии.
Задание 5. Запишите характеристическое свойство геометрической прогрессии.
Ответы:
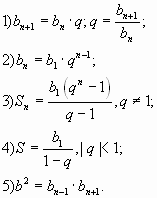
Дополнительный вопрос: Дать определение геометрической прогрессии и привести пример.
Выставление оценок в листы самоконтроля по количеству верных ответов по 5-бальной шкале.
IV. Работа с тестом.
Тест “Установите, истинны или ложны следующие утверждения”:
Задание 1. Последовательность, заданная формулой bn = 32n, - геометрическая прогрессия.
Решение:
![]()
Ответ: да.
Задание 2. Третий член геометрической
прогрессии, у которой ![]() равен -18.
равен -18.
Решение:
![]()
Ответ: нет.
Задание 3. Сумма семи первых членов геометрической прогрессии, у которой b1 = 3, q = 2, равна 384.
Решение:
![]()
Ответ: нет.
Задание 4. Геометрическая прогрессия,
заданная формулой ![]() , является бесконечно убывающей.
, является бесконечно убывающей.
Решение:
![]()
Ответ: нет.
Задание 5. Сумма бесконечно убывающей
геометрической прогрессии равна ![]() , если
, если
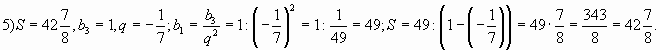
Решение:
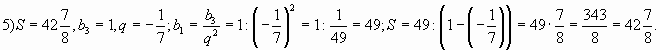
Ответ: да.
Проверка через видеопроектор и выставление оценок в листы самоконтроля по количеству верных ответов по 5-бальной шкале.
V. Решение задач из сборника экзаменационных заданий ГИА.
Задача 1. Сумма первых трех членов геометрической прогрессии равна 9, а сумма следующих трех ее членов равна -72. Найдите восьмой член этой прогрессии.
Решение:
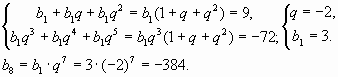
Ответ: -384.
Задача 2. Существует ли геометрическая
прогрессия, в которой ![]()
Решение:
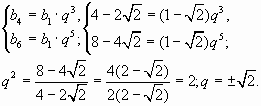
Ответ: да.
Задача 3. Является ли число 64 членом геометрической прогрессии 0,5; 1; ...?
Решение:
![]()
Ответ: да.
Задача 4. Найдите сумму бесконечно убывающей геометрической прогрессии bn, если b2 - b4 = 3 и b1 - b3 = 6.
Решение:
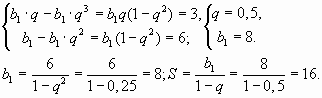
Ответ: 16.
Задача 5. При каком целом значении х последовательность х, х + 2, 5х – 2 является геометрической прогрессией?
Решение:
Согласно характеристическому свойству геометрической прогрессии имеем: (х + 2)2 = х(5х – 2).
Откуда х = - 0,5 – число не целое и х = 2 – число целое.
Ответ: 2.
Выставление оценок в листы самоконтроля по количеству верных ответов по 5-балльной шкале.
VI. Решение познавательных задач.
Задача 1. Один биолог “открыл” удивительную разновидность амеб. Каждая из них через минуту делится на две. В пробирку биолог кладет одну амебу, и ровно через час вся пробирка оказывается заполненной амебами. Сколько потребовалось бы времени, чтобы вся пробирка заполнилась амебами, если бы в нее положили вначале не одну, а две?
Решение:
Запишем две геометрические прогрессии одна под другой:
1; 2; 4; 8; 16; 32; ... и
2; 4; 8; 16; 32;...
Тогда очевидно, что задача решается с конца. Минуту назад колба с одной амебой была заполнена наполовину. Следовательно, нужно 59 минут, чтобы вся пробирка заполнилась амебами, если бы в нее положили вначале не одну, а две.
Ответ: 59 минут.
Задача 2. Построить график геометрической прогрессии 1; 2; 4; 8; 16;... .
Решение:
b1 = 1; q = 2; bn = b1* qn – 1 = (b1 : q) * qn = 0,5 * qn .
Заполним таблицу и нанесем точки на систему координат.
| n | 1 | 2 | 3 | 4 | 5 |
| bn= 0,5 * 2n | 1 | 2 | 4 | 8 | 16 |
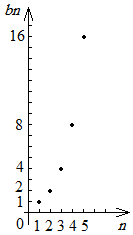
Получаем точечный график. Точки графика лежат на кривой, которую в 10-м классе при изучении показательной функции назовем экспонентой.
VII. Задание на дом.
Задачи из учебника и сборника ГИА по теме “Геометрическая прогрессия”.
VIII. Итог урока.
Учащиеся оценивают свою работу как среднее арифметическое трех оценок, выставленных в листках самоконтроля.
Называются самые трудные задания, которые вызвали затруднения для дальнейшей коррекции на следующем уроке.
Примечание. Учащиеся обучаются по учебнику для общеобразовательных учреждений: Алгебра. 9 класс: учеб. для общеобразоват. учреждений / [Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова]; под ред. С.А. Теляковского. – 18-е изд. - М.: Просвещение, 2011.