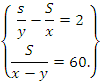Тип урока: повторительно-обобщающий урок.
Цели урока:
- образовательные – повторить методы решения различных типов текстовых задач на движение
- развивающие – развивать речь учащихся через обогащение и усложнение её словарного запаса, развивать мышление учащихся через умение анализировать, обобщать и систематизировать материал
- воспитательные – формирование гуманного отношения у учащихся к участникам образовательного процесса
Оборудование урока:
- интерактивная доска;
- конверты с заданиями, картами тематического контроля, карточками – консультантами.
Структура урока.
№ |
Основные этапы урока |
Задачи, решаемые на данном этапе |
Время |
1 |
Организационный момент, вводная часть |
|
2 мин |
2 |
Подготовка учащихся к активной работе (повторение) |
|
7 мин |
3 |
Этап обобщения и систематизации изученного материала (работа в группах) |
|
25 мин |
4 |
Проверка выполнения работы, корректировка (при необходимости) |
|
8 мин |
5 |
Подведение итогов урока. Разбор домашнего задания |
|
3 мин |
Формы организации познавательной деятельности учащихся:
- фронтальная форма познавательной деятельности – на этапах II, IY, Y.
- групповая форма познавательной деятельности – на III этапе .
Методы обучения: словесный, наглядный, практический, объяснительно – иллюстративный, репродуктивный, частично – поисковый, аналитический, сравнительный, обобщающий, традуктивный.
Ход урока
I. Организационный момент, вводная часть.
Учитель объявляет тему урока, цели урока и основные моменты урока. Проверяет готовность класса к работе.
II. Подготовка учащихся к активной работе (повторение)
Ответьте на вопросы.
- Какое движение называют равномерным (движение с постоянной скоростью).
- Назовите формулу пути при равномерном движении (S = Vt).
- Из этой формулы выразите скорость и время.
- Указать единицы измерения.
- Перевод единиц измерения скорости
S |
V |
t |
км |
км/ч |
ч |
м |
м/с |
с |
м |
м/мин |
мин |
А) ![]()
![]()
![]()
![]()
![]()
III. Этап обобщения и систематизации изученного материала (работа в группах)
Весь класс разбивается по группам (5-6 человек в группе). Желательно, чтобы в одной группе были учащиеся разного уровня подготовки. Среди них назначается руководитель группы (самый сильный учащийся), который и будет руководить работой группы.
Все группы получают конверты с заданиями (они одинаковы для всех групп), карточки консультанты (для слабых учащихся) и листы тематического контроля. В листах тематического контроля руководитель группы выставляет оценки каждому учащемуся группы за каждое задание и отмечает затруднения, которые возникли у учащихся при выполнении конкретных заданий.
Карточка с заданиями для каждой группы.
№ 1. Из двух городов, расстояние между которыми равно 480 км, навстречу друг другу одновременно выехали два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны 75 км/ч и 85 км/ч?
№ 2. Из городов A и B, расстояние между которыми равно 330 км, навстречу друг другу одновременно выехали два автомобиля и встретились через 3 часа на расстоянии 180 км от города B. Найдите скорость автомобиля, выехавшего из города A. Ответ дайте в км/ч.
№ 3. Из пункта А в пункт В, расстояние между которыми 50 км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на 65 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 4 часа 20 минут позже автомобилиста. Ответ дайте в км/ч.
№ 4. Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого?
№ 5. Из одной точки круговой трассы, длина которой равна 12 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 101 км/ч, и через 20 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
№ 6. Из пункта A круговой трассы выехал велосипедист, а через 40 минут следом за ним отправился мотоциклист. Через 8 минут после отправления он догнал велосипедиста в первый раз, а еще через 36 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч.
№ 7. Моторная лодка прошла против течения реки 112 км и вернулась в пункт отправления, затратив на обратный путь на 6 часов меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 11 км/ч. Ответ дайте в км/ч.
№ 8. Теплоход проходит по течению реки до пункта назначения 513 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 4 км/ч, стоянка длится 8 часов, а в пункт отправления теплоход возвращается через 54 часа после отплытия из него. Ответ дайте в км/ч.
№ 9. От пристани А к пристани В, расстояние между которыми равно 168 км, отправился с постоянной скоростью первый теплоход, а через 2 часа после этого следом за ним, со скоростью на 2 км/ч большей, отправился второй. Найдите скорость первого теплохода, если в пункт В оба теплохода прибыли одновременно. Ответ дайте в км/ч.
Образец карточки тематического контроля.
| Класс ________ Ф.И.учащегося___________________________________ | ||
№ задания |
Оценка |
Замечание |
1 |
||
2 |
||
3 |
||
4 |
||
5 |
||
6 |
||
7 |
||
8 |
||
9 |
||
Карточки консультанты.
| Карточка № 1 (консультант) |
| 1. Движение по прямой дороге |
| При решении задач на равномерное
движение часто встречаются две ситуации. Если начальное расстояние между объектами равно S , а скорости объектов V1 и V2, то: а) при движении объектов навстречу друг другу
время, через которое они встретятся, равно б) при движении объектов в одну сторону время,
через которое первый объект догонит второй,
равно |
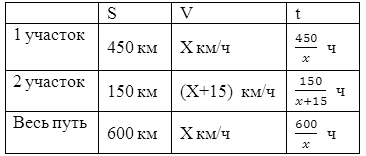
| Пример 1. Поезд, пройдя 450 км, был
остановлен из-за снежного заноса. Через полчаса
путь был расчищен, и машинист, увеличив скорость
поезда на 15 км/ч, привел его на станцию без
опоздания. Найдите первоначальную скорость
поезда, если путь, пройденный им до остановки,
составил 75% всего пути. Решение.
Решение:
Х= -75 не подходит по условию задачи, где x > 0. Ответ: первоначальная скорость поезда равна 60 км/ч. |
| Карточка № 2 (консультант) |
2. Движение по замкнутой дороге |
| Если длина замкнутой дороги равна S ,
а скорости объектов V1 и V2, то: а)
при движении объектов в разных направлениях
время между их встречами вычисляется по формуле |
| Пример 2. На соревнованиях по
кольцевой трассе один лыжник проходит круг на 2
мин быстрее другого и через час обошел его ровно
на круг. За какое время каждый лыжник проходит
круг? Решение. Пусть S м – длина кольцевой трассы и x м/мин и y м/мин – скорости первого и второго лыжников соответственно (x > y) . Тогда S/x мин и S/y мин – время, за которое
проходит круг первый и второй лыжники
соответственно. Из первого условия получаем
уравнение Решим систему уравнений.
Сделаем замену S/x= a и S/y= b, тогда система уравнений примет вид:
60(a + 2) – 60a = a(a + 2) Ответ: 10 мин; 12 мин. |
| Карточка № 3 (консультант) |
3. Движение по реке |
| Если объект движется по течению реки, то
его скорость равна Vпо теч. =Vсоб. +Vтеч. Если
объект движется против течения реки, то его
скорость равна Vпротив теч =V соб. – Vтеч. Собственная
скорость объекта (скорость в неподвижной воде)
равна Скорость течения реки равна Скорость движения плота равна скорости течения реки. |
| Пример 3. Катер спустился вниз по
течению реки на 50 км, а затем прошел в обратном
направлении 36 км, что заняло у него на 30 минут
больше времени, чем по течению. Какова
собственная скорость катера, если скорость
течения реки 4 км/ч? Решение. Пусть собственная скорость катера равна х км/ч,
тогда его скорость по течению реки равна (x + 4)
км/ч, а против течения реки (x - 4) км/ч. Время
движения катера по течению реки равно Получим 72(x + 4) -100(x - 4) = (x + 4)(x - 4) Итак, собственная скорость катера равна 16 км/ч. Ответ: 16 км/ч. |
IV. Этап разбора решения задач.
Разбираются задачи, вызвавшие у учащихся затруднение.
№ 1. Из двух городов, расстояние между которыми равно 480 км, навстречу друг другу одновременно выехали два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны 75 км/ч и 85 км/ч?
Решение.
- 75 + 85 = 160 (км/ч) – скорость сближения.
- 480 : 160 = 3 (ч).
Ответ: автомобили встретятся через 3 часа.
№ 2. Из городов A и B, расстояние между которыми равно 330 км, навстречу друг другу одновременно выехали два автомобиля и встретились через 3 часа на расстоянии 180 км от города B. Найдите скорость автомобиля, выехавшего из города A. Ответ дайте в км/ч.
Решение.
- (330 – 180) : 3 = 50 (км/ч)
Ответ: скорость автомобиля, выехавшего из города A равна 50 км/ч.
№ 3. Из пункта А в пункт В, расстояние между которыми 50 км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на 65 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 4 часа 20 минут позже автомобилиста. Ответ дайте в км/ч.
Решение.
Составим таблицу.
S (км) |
V (км/ч) |
t (ч) |
|
велосипедист |
50 |
|
|
автомобилист |
50 |
х+65 |
|
Составим уравнение, учитывая, что 4 часа 20 минут
= ![]()
![]()
![]()
Очевидно, что х = -75 не подходит по условию задачи.
Ответ: скорость велосипедиста 10 км/ч.
№ 4. Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого?
Решение.
Составим таблицу.
t (ч) |
V (км/ч) |
S (км) |
|
1 мотоциклист |
t |
|
t x |
2 мотоциклист |
t |
х+21 |
t(x +21) |
Cоставим уравнение.
![]()
Ответ: через 20 минут мотоциклисты поравняются в первый раз.
№ 5. Из одной точки круговой трассы, длина которой равна 12 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 101 км/ч, и через 20 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
Решение.
Составим таблицу.
t (ч) |
V (км/ч) |
S (км) |
|
1 автомобиль |
20мин=1/3 ч |
101 |
|
2 автомобиль |
20мин=1/3 ч |
х |
|
Составим уравнение.
![]()
Ответ: скорость второго автомобиля 65 км/ч.
№ 6. Из пункта A круговой трассы выехал велосипедист, а через 40 минут следом за ним отправился мотоциклист. Через 8 минут после отправления он догнал велосипедиста в первый раз, а еще через 36 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч.
Решение.
Составим таблицу.
Движение до первой встречи |
|||
t (ч) |
V (км/ч) |
S (км) |
|
велосипедист |
|
х |
|
мотоциклист |
|
у |
|
Первое уравнение составим по таблице ![]() , так как
расстояние, пройденное до первой встречи и
мотоциклистом и велосипедистом будет
одинаковое.
, так как
расстояние, пройденное до первой встречи и
мотоциклистом и велосипедистом будет
одинаковое.
Второе уравнение составим из условия второй
встречи: ![]()
Решим систему уравнений: 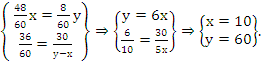
Ответ: скорость мотоциклиста 60 км/ч.
№ 7. Моторная лодка прошла против течения реки 112 км и вернулась в пункт отправления, затратив на обратный путь на 6 часов меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 11 км/ч. Ответ дайте в км/ч.
Решение.
Составим таблицу, исходя их условия, что скорость течения реки равна х км/ч.
V (км/ч) |
S (км) |
t (ч) |
|
По течению |
11 + х |
112 |
|
Против течения |
11 – х |
112 |
|
Составим уравнение: ![]()
Умножая обе части уравнения на ![]()
![]()
![]()
где ![]()
Ответ: скорость течения реки равна 3 км/ч.
№ 8. Теплоход проходит по течению реки до пункта назначения 513 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 4 км/ч, стоянка длится 8 часов, а в пункт отправления теплоход возвращается через 54 часа после отплытия из него. Ответ дайте в км/ч.
Решение.
Составим таблицу, исходя их условия, что собственная скорость теплохода равна х км/ч.
V (км/ч) |
S (км) |
t (ч) |
|
По течению |
Х + 4 |
513 |
|
Против течения |
Х – 4 |
513 |
|
Составим уравнение: ![]()
Умножая обе части уравнения на ![]()
![]()
![]()
где ![]()
Ответ: собственная скорость теплохода равна реки 23 км/ч.
№ 9. От пристани А к пристани В, расстояние между которыми равно 168 км, отправился с постоянной скоростью первый теплоход, а через 2 часа после этого следом за ним, со скоростью на 2 км/ч большей, отправился второй. Найдите скорость первого теплохода, если в пункт В оба теплохода прибыли одновременно. Ответ дайте в км/ч.
Решение.
Составим таблицу, исходя их условия, что скорость первого теплохода равна х км/ч.
V (км/ч) |
S (км) |
t (ч) |
|
I теплоход |
Х |
168 |
|
II теплоход |
Х +2 |
168 |
|
Составим уравнение: ![]()
Умножая обе части уравнения на х![]()
![]()
![]()
где ![]()
Ответ: скорость первого теплохода равна реки 12 км/ч
V. Подведение итогов урока.
Во время подведения итогов урока ещё раз следует обратить внимание учащихся на принципы решения задач на движение. При даче домашнего задания дать пояснение к наиболее трудным задачам.
Литература.
1) Статья: Математика ЕГЭ 2014 (система задач из открытого банка заданий) Корянов А.Г., Надежкина Н.В. – опубликована на сайте http://alexlarin.net/