Роль уроков статистики в укреплении базовых знаний, умений и навыков школьников по математике в основной школе

Включение уроков статистики в школьную программу значительно обогатило возможности математического развития детей. С этим предметом пришли на урок практические задачи, насыщенные богатейшим жизненным содержанием.

Мы осваиваем с вами, коллеги, новые формы проверки знаний, умений и навыков школьников по математике: единый государственный экзамен (ЕГЭ) в средней школе и государственную итоговую аттестацию (ГИА) в основной школе. И тут выяснилось, что некоторые наши дети, успешно освоившие алгоритмы решения непростых уравнений, навыки дифференцирования и интегрирования, вдруг растерялись и не смогли справиться с элементарными задачами на покупку билетов по новой цене, на повышение/понижение стоимости товара, не говоря уже о банковских расчётах и анализе ситуаций на фондовом рынке. А всё потому, что, перефразируя классика, “страшно далека наша школьная математика от народа”.

Благодаря урокам статистики у нас появилась ещё и дополнительная возможность совершенствовать вычислительную культуру школьников. Выпускников основной школы, умеющих ответственно, аккуратно, терпеливо считать, следует отнести к категории достояния Республики.

Есть и наша вина в том, что дети не чувствуют своей ответственности за качество вычислений. Что греха таить, мы сами ставим ученику “4” или “5”, если он составил алгоритм поиска ответа на вопрос задачи, но не довёл вычисления до верного ответа. Вычислительную ошибку и “недовычисление” надо отнести к разряду грубых ошибок.

Приглашаю на урок статистики в 7 класс по материалу Главы III учебника [1].

Тема урока “Среднее значение”

Начиная урок, призываю детей открыть учебник на странице 44. Ученики сначала читают текст до слова Определение. Определение прошу прочесть вслух. Повторим математическое понятие “отношение”. Обратим внимание на тот важный арифметический факт, что сумма всех чисел набора равна произведению их среднего арифметического на количество чисел в наборе.

Решим устно такую задачу: среднее арифметическое четырёх чисел равно 7; можем ли мы, не видя этих чисел, найти их сумму?

Ответ. Да, 7 * 4 = 28.

Вопрос. Мог это быть набор 5; 10; 6; 7?

Ответ. Да, потому что сумма всех данных набора 28, и среднее 28:4 =7.

Придумайте ещё какой-нибудь набор из четырёх чисел, у которых среднее арифметическое равно 7.

Возможные варианты ответа: 5; 10; 4; 9 или 7; 7; 7; 7.

Далее проецируем на экран Таблицу 1 со страницы 44 пособия [1].

Продолжаем учить детей считыванию информации из таблицы (этот навык нарабатывался на предыдущих уроках). Задаём вопросы.

Как называется эта таблица?

Ответ. Производство пшеницы в России в 1995-2001 гг.

За сколько лет отражает эта таблица производство пшеницы в России?

Ответ. За семь лет.

Конечно, большинство семиклассников пальчиком посчитали количество столбиков и получили 7 дат. Но всё же обращаю внимание на то, что подсчёт количества дат последовательно идущих лет проводят так: 2001-1995+1=7. Это чрезвычайно важный арифметический факт. Помните, как нередко путают количество вбитых колышков по направлению прямой линии и количество промежутков между колышками?

Продолжаю задавать вопросы.

Как вы думаете, почему так различны показатели производства пшеницы в разные годы? Найдите ответ в учебнике, подумайте сами. Осмысленные фантазии на тему поощряются.

Сколько миллионов тонн пшеницы было произведено в России в 1998 году?

Ответ. В 1998 году произведено 27,0 млн. тонн пшеницы.

Найдётся ученик, который скажет: “А какая разница 27 просто, или 27,0?”

Напомню детям, что в таблице отражены приближённые значения величины. Округления произведены с точностью до 0,1, о чём и говорит наличие этого десятичного знака, пусть даже нуля.

Сколько миллионов тонн пшеницы было произведено в России в 2001 году?

Ответ. 47,0 млн. тонн.

Уместно задать провокационный вопрос: “Может, отбросим цифру 0?”

На сколько выросло производство пшеницы в 2001 году по сравнении с 1998 годом?

Ответ. На 20,0 млн. тонн.

Чем же так коварен оказался 1998 год?

На этот вопрос дети не ответят. Не найдут они ответа и в учебнике.

Учитель: “Это связано с дефолтом российской экономики, произошедшим в августе 1998 года. Банкротство банков, кредитовавших сельскохозяйственную отрасль, резкое сокращение инвестиций в отрасль, общее обесценивание денежных активов – всё это повлияло на сельское хозяйство. Одни предприятия прекратили своё существование, другие резко сократили производственные мощности”.

Продолжаю учить семиклассников поиску информации из таблицы.

Дети устно отвечают на вопросы с 1 по 4 из упражнения на стр. 45.

Затем решим устно:

№5а. Вычислите среднее арифметическое чисел 8 и 10.

№5б. Вычислите среднее арифметическое чисел 8; 9 и 10.

Ещё раз попрошу Павлика прочитать определение среднего арифметического вслух. “Согласно этому определению:

а) (8 + 10)/2 =9”, - комментирует ученик;

“…б) (8 + 9 + 10) / 3 = 9”, - комментирует другой.

Смотрите, ребята: ответ получился один и тот же? Заметим, что если к набору из двух чисел добавить их среднее арифметическое, то новое среднее арифметическое уже трёх чисел будет точно таким же. В наборе 8; 10 восьмёрка и десятка дают в сумме два своих средних арифметических. Значит, если добавить к ним их же среднее (8; 9; 10), то новая сумма будет равна уже трём средним значениям.

А кто быстро посчитает среднее арифметическое набора 8; 10; 9; 9; 9; 9; 9; 9; 9; 9?

Не тратя времени на вычисление, дети дают правильный ответ 9.

Решим устно задание №7 на странице 46: “Все числа равны между собой. Чему равно их среднее арифметическое?”

Дети назовут свои наборы равных чисел. Юля назвала: 5; 5; 5; 5. Произнесла определение среднего арифметического (или прочитала нам его в учебнике), затем посчитала (5 +5 +5 +5)/4 =20/4=5

“Значит, если числа набора равны между собой, то …”. Предвижу ситуацию, что учитель сам произнесёт этот вывод, чтобы поскорее двигаться дальше. Не упускайте каждый раз ценнейшую возможность учить детей математической речи и тем самым развивать математическое мышление. Надо побуждать детей к говорению, комментированию; решение “молча”, пусть и правильное, мало способствует развитию школьников. Навыки монологической речи им пригодятся и на других уроках.

Семиклассники только - только начали изучать систематический курс алгебры; покажем применение алгебры к доказательству свойств чисел в общем виде: (a+a+a+…+a):n = na : n =a.
                                 n слагаемых

По ходу нахождения среднего для набора чисел обращаем внимание школьников на тот факт, что среднее всегда получается не меньше меньшего числа набора, но не больше большего числа набора. При самоконтроле за результатами подсчёта среднего это знание пригодится.

Обсудим устно такую задачу. При вычислении среднего для числового набора 2; 4,8; 0,06; 7,94; 5,2 Юрий получил 0,052; Саша получил 8,2; у Олега вышло 4. Кто из них прав?

Ответ. У Юры среднее меньше меньшего числа – он не прав; у Саши среднее оказалось больше большего числа. Он ошибся. Правдоподобен ответ Олега, но всё же проверим… Да, он прав!

Проведём самостоятельную работу. Предлагаем две задачи из [1].

№11а - “Вычислите среднее арифметическое чисел 1, 2, 3, 4, 5”. Ответ: 3.

№11г - “ Вычислите среднее арифметическое чисел 1, 2, 3, 4, 1000”. Ответ: 202.

Сколько чисел в каждом наборе? - По пять чисел в каждом наборе.

А чем отличаются эти два набора? – Во втором наборе последнее пятое число намного больше, чем пятое число в первом наборе.

Почему у второго набора среднее оказалось значительно больше, чем у первого набора?

Один из вариантов ответа (но только не опережайте детей): “Если хотя бы одно из чисел набора увеличить, то непременно увеличится и среднее этого набора”.

На каждой парте лежит листок с заготовленными заранее числовыми прямыми, и мы отметим на них только что рассмотренные наборы чисел. Число 1000 на второй числовой прямой условно отметим как можно правее. Покажем средние каждого набора.

1 2 3 4 5

1 2 3 4         202     1000

Заметим, что в первом наборе среднее значение 3 оказалось среди чисел набора, а во втором ряду среднее 202 таковым не является. Когда мы на следующем уроке будем говорить об устойчивости медианы и подвижности среднего, нам этот пример очень пригодится.

Спасибо уроку статистики, предоставившему нам возможность напомнить задачи на нахождение среднего из курса арифметики 5-6 класса. По-новому посмотрим сегодня на ситуации таких задач, на оформление решений.

Задача 1. Смешали 2 кг карамели “Калинка” по цене 30 рублей за килограмм и 3кг карамели “Малинка” по цене 25 рублей. Как правильно рассчитать цену килограмма смеси “Калинка-Малинка”?

Решение. Запишем набор величин – это цены за каждый килограмм смешиваемых конфет: 30 руб.; 30 руб.; 25 руб.; 25 руб.; 25 руб.

Найдём среднее этого набора: (30*2 + 25*3): 5= 135:5 =27

Ответ. Цена смеси 27 рублей за килограмм.

Задача 2. От пункта А до пункта В мотоциклист ехал 2 часа со скоростью 40км/ч. В пункте В ему пришлось 2 часа ремонтировать своего “железного коня”, а потом от В до С он ехал 3 часа со скоростью 55 км/ч. Требуется вычислить среднюю скорость движения мотоциклиста на всём пути от А до С.

Решение. Запишем набор значений скоростей, соответствующих каждому часу его путешествия: 40 км/ч; 40 км/ч; 0 км/ч; 0 км/ч; 55 км/ч; 55 км/ч; 55 км/ч.

Осталось найти среднее числового набора (40+40+0+0+55+55+55): 7 =245:7 = 35. Ответ. Средняя скорость движения мотоциклиста на всём пути от А до С 35 км/ч.

Задача 3. Смешали 4 кг 13%-го раствора поваренной соли с 2 кг 7%-го раствора поваренной соли. Найти концентрацию поваренной соли в получившейся смеси.

Решение. Перечислим набор концентраций соли в каждом килограмме смешиваемых растворов: 13% , 13%, 13%, 13%, 7%, 7%. Среднее значение набора 66% : 6 = 11%.

Ответ. Получили 11%-ый раствор поваренной соли.

Вижу, коллеги, кому-то такое оформление решений показалось неоправданно упрощённым. Но усложнить и условия, и решения вы ещё успеете, а такой подход к задаче о вычислении среднего понятен даже самому слабому ученику.

Теперь представим, что числовая ось является стержнем, на который подвешены гири одинаковой массы в точках, соответствующих данным числам:

17; 21; 22; 24; 25; 26; 29; 32; 35; 39.

 

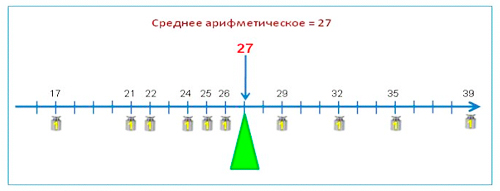
Равновесие установится только тогда, когда точка опоры совпадёт со средним значением. Воспользовавшись программой Живая Математика и курсом статистики iкласса, наши семиклассники имеют возможность на экранах своих компьютеров подвигать опору стержня до установления равновесия.

Завершаем урок выполнением самостоятельной работы: из учебника стр. 47 №17.

I-й вариант отвечает на вопрос (а), II вариант отвечает на вопрос (б).

Мотивированные школьники успеют выполнить №13 (а, г).

Намереваясь создать интригу следующего урока, объявляю напоследок, что иногда средние характеристики могут ввести нас в заблуждение.

Например, помечтаем о космическом путешествии. Может, полетим на Меркурий? Средняя температура на планете Меркурий равна +15°С, - вполне пригодно для жизни! Но!.. Температура в течении суток там колеблется от –150°С до + 350°С. Значит, бывают такие числовые данные, что для обоснованных выводов или надёжных прогнозов необходимо помимо средних указывать и другие сведения о наборе данных. С этими новыми характеристиками наборов данных я и познакомлю семиклассников на следующих уроках статистики.

Задание на дом:

а) раздаю по одному конверту с числовыми наборами, прошу к следующему уроку вычислить среднее этого набора; на последующих уроках мы решим несколько разнообразных заданий с этими наборами; б) составить и решить задачу, аналогичную одной из последних трёх, разобранных в классной работе;

в) раздаю карточки с задачей, не обязательной для всех, но полезной заинтересованным школьникам.

Задача в). Семеро друзей: Аня, Борис, Володя, Герман, Даша, Елена и Жора живут вдоль шоссе, которое проложено в лесу. В каком месте шоссе им необходимо собраться на пикник, чтобы суммарно израсходовать на путешествие минимальное количество денег на бензин? Будем считать, что любое место в лесу недалеко от шоссе является прекрасным местом для пикника.

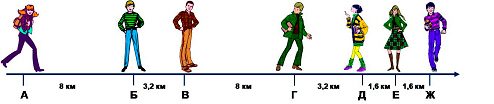
Для коллег привожу один из вариантов решения этой задачи.

Решение. Нужно выбрать на шоссе такую точку, чтобы сумма расстояний от точек А, Б, В, Г, Д, Е и Ж до этой точки была минимальной. Введём координатную прямую, направив её вдоль прямой, изображающей шоссе; за начальную точку примем точку А, направление - в сторону точки Б. Тогда координаты станут такими: А(0), Б(8), В(11,2), Г(19,2), Д(22,4), Е(24), Ж(25,6)

Может быть, следует найти среднее арифметическое координат и подсчитать сумму расстояний до соответствующей точки? Попробуем.

Среднее

Сумма расстояний от всех точек до точки с координатой 15,8 равна 15,8 + 7,8 + 4,6 + 3,4 + 6,6 + 8,2 + 9,8 = 56,2 (км).

А что, если встретиться посередине между Аней и Жорой – в точке с координатой 12,8? Увы, суммарное расстояние, которое проедут друзья, тогда будет 59,2 км!

Оказывается, что сумма расстояний от всех точек до точки с координатой, равной медиане координат друзей, является более предпочтительной. Медианой является точка Г(19,2).     

В этом случае сумма расстояний, которую должны проехать друзья, равна

19,2 + 11,2 + 8 + 0 + 3,2 + 4,8 + 6,4 = 52,8 (км). О медиане ученики узнают на следующем уроке.

На занятии кружка можно переформулировать задачу и найти точку минимума кусочно-линейной функции f(x)=|x|+|8-x|+|11,2-x|+|19,2-x|+|22,4-x|+|24-x|+|25,6-x|. Ответ: х_min=19,2.

Литература

1. Преподавание математики в 2009/2010 учебном году. Методическое письмо/под ред. И.В. Ященко, А.В. Семёнова – М.: МИОО, 2009.
2. Теория вероятностей и статистика / Ю.Н.Тюрин, А.А.Макаров, И.Р. Высоцкий, И.В. Ященко. – 2-е изд., переработанное. – М.: МЦНМО: ОАО “Московские учебники”, 2008 /Учебное пособие для учащихся 7-9 классов.
3. Теория вероятностей и статистика. Методическое пособие для учителя/ Ю.Н.Тюрин, А.А. Макаров, И.Р. Высоцкий, И.В. Ященко . – 2-е изд., исправленное и дополненное. – М.: МЦНМО: МИОО, 2008.
4. Вероятность: примеры и задачи /А. Шень/ - 2-е издание, стереотипное. –М.: МЦНМО, 2008.