Ход урока
Учитель: (на экране Слайд 1.)
Альберт Эйнштейн сказал замечательные слова, вслушайтесь в них: “Ощущение тайны – наиболее прекрасное из доступных нам переживаний. Именно это чувство стоит у колыбели истинного искусства и настоящей науки”.
Вот и мы сегодня с вами в очередной раз попытаемся приоткрыть одну из тайн, которую дарит нам наука. Тема нашего сегодняшнего урока: учитель зачитывает тему и цель урока.
Цель:
- Познакомиться с понятием иррациональные уравнения и некоторыми методами их решения.
- Развивать умение выделять главное в изучаемом материале, обобщать факты и понятия.
Учитель:
– Чтобы лучше усвоить новую тему, вспомним пройденный материал.
– Сегодня на уроке мы работаем, разбившись на группы (класс делится на 4 группы
по 6-7 человек, на столе у каждой группы флажок с номером).
I. Устная работа.
Учитель дает задание:
Разложить на множители: (Cлайд 3).
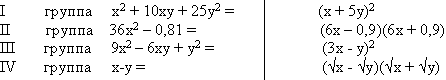
Затем даются ответы на экране.
Для последней из группы учитель просит разложить разность (х – у), используя
формулу сокращенного умножения: разность квадратов.
Далее на слайде появляется дополнительный вопрос:
Доп. Вопрос (√16)2 = ? (16)
Отвечает любой учащийся.
Учитель озвучивает следующее задание: Найти область определения. (Слайд 4).
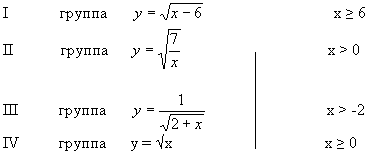
После ответов учащихся высвечиваются ответы на слайде.
Дополнительный вопрос на слайде появляется последним, один из учеников его
зачитывает:
Доп. Вопрос: Из последнего промежутка найти наименьшее положительное целое число
(1)
Учитель: В школьном курсе алгебры рассматриваются различные виды уравнений:
Слайд 5.
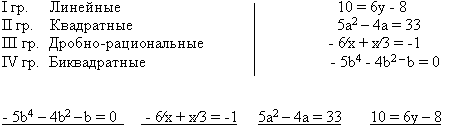
Каждая из групп выбирает нужное уравнение. После ответов высвечиваются уравнения.
Доп. Вопрос: Является ли число 3 решением вашего уравнения?
В чью группу войдет уравнение х2 = 4. Решите его.
Учитель: Является ли число Хо – корнем вашего уравнения?
Слайд 6.
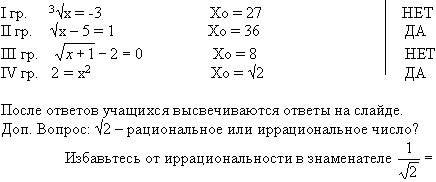
Учитель: А сейчас небольшая историческая справка, (выходит учащийся и рассказывает наизусть):
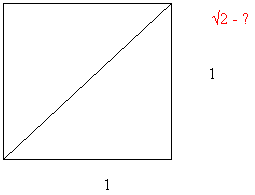
История иррациональных чисел восходит к удивительному открытию Пифагорийцев ещё в VI веке до н.э. А началось все с простого, казалось бы вопроса – каким числом выражается длина диагонали квадрата со стороной 1?
Пифагорийцы доказали, что √2 – нельзя выразить отношением некоторых целых чисел m и n. √2 – по их мнению вообще не было числом. Открыв новый математический объект они пришли в полное замешательство. В основе всеобщей гармонии мира, считали они, должны лежать целые числа и их отношения. Никаких других чисел они не знали. И вдруг эта гармония рушится – существуют величины, которые отношением целых чисел, в принципе – не являются.
В переводе с латыни “irrationalis” – “неразумный”. Любопытно, что в средневековой Европе наряду с “irrationalis” в ходу был еще и другой термин “surdus” – “глухой” или “немой”. Судя по такому названию, математикам средневековья иррациональные числа представлялись чем-то настолько “неразумным”, что “ни высказать, ни выслушать”. Удивление и досада, с которыми древние математики в начале восприняли иррациональные числа, впоследствии, сменились интересом и пристальным вниманием к новым математическим объектам.
“История иррациональных чисел”. (Слайд 7).
В переводе с латыни “irrationalis” – “неразумный”.
“surdus” – “глухой” или “немой”. “ни высказать, ни выслушать”.
Учитель: Вот и мы сейчас с таким же интересом и вниманием обратимся не к иррациональным числам, но к иррациональным уравнениям. Открываем тетради, записываем тему урока: “Иррациональные уравнения”.
Слайд 8.
Высвечивается определение: Уравнения, в которых переменная содержится под знаком корня называются иррациональными.
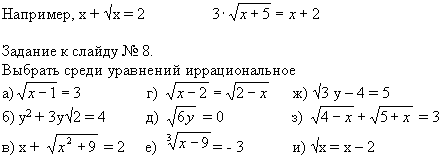
Записать в тетрадь последнее уравнение: √х = х – 2
Оно же и на доске.
Один из учащихся выходит его решать.
Учитель: Методы решения иррациональных уравнений, как правило, основаны на возможности перехода от иррационального к рациональному уравнению. Рассмотрим один из методов: возведение в степень обеих частей уравнения.
Ребята, т.к. мы с вами выпускной класс и впереди предстоит сдача ЕГЭ, наша задача подготовиться к нему. Поэтому те уравнения, которые мы будем разбирать на уроке, взяты из разных сборников для подготовки к ЕГЭ.
II. Работа в тетрадях.
а) Решить уравнение: Вопросы к учащемуся, который решает это уравнение:

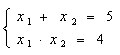
х1 = 1, х2 = 4
Оба корня проверяем, подставляя в исходное уравнение. Видим, что х1 = 1 – не является корнем исходного уравнения, закрываем его магнитом на доске [посторонний корень].
Ответ: 4

Возведя обе части уравнения в нечетную степень, перешли к равносильному
уравнению.
– Нужна ли проверка в данном случае?
– Может ли появиться посторонний корень?
– Корень проверяется, чтобы исключить арифметическую ошибку.
Слайд 9.
При возведении обеих частей уравнения:
- в четную степень (показатель корня – четное число), возможно появление постороннего корня (проверка необходима);
- в нечетную степень (показатель корня – нечетное число), получается уравнение, равносильное исходящему, (проверка не нужна).
Учитель: Иногда удобнее решать иррациональные уравнения, используя равносильные преобразования, определить ОД3. (В этом случае проверку делать не надо).
На доске: Вопрос к учащемуся у доски:
г)
![]() = х – 1 – Вспомнить определение арифметического корня n-ой степени.
= х – 1 – Вспомнить определение арифметического корня n-ой степени.
![]() = х – 1
= х – 1
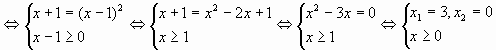
X2 = 0 посторонний корень.
Ответ: 3
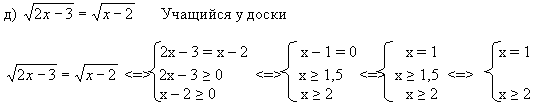
Ответ: Решений нет.
Слайд 10.
Решая иррациональные уравнения, используя равносильные преобразования – проверка не нужна.
е) Уравнение, предлагаемое к самостоятельному решению.

Проверка: Подходят оба.
Ответ: ±1
Один ученик вызывается к доске для проверки, рассказывает ход решения.
III. Самостоятельная работа.
Слайд 11.
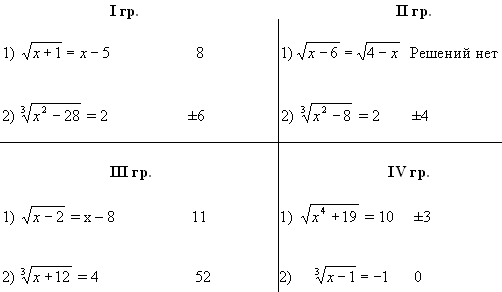
После решения и сдачи самостоятельных работ на слайде появляются ответы.
Слайд 12.
Итог урока:
– Иррациональные уравнения?
При возведении обеих частей уравнения:
- в четную степень (показатель корня – четное число), возможно появление постороннего корня (проверка необходима);
- в нечетную степень (показатель корня – нечетное число), получается уравнение, равносильное исходящему, (проверка не нужна).
Учитель: Иногда удобнее решать иррациональные уравнения, используя равносильные преобразования, определить ОД3. (В этом случае проверку делать не надо).
Решая иррациональные уравнения, используя равносильные преобразования – проверка не нужна.
Учитель подводит итог урока глядя на слайд, опрашивая учащихся, благодарит за урок и говорит о том, что на следующем уроке познакомит ребят с другими методами решения замены переменной.
Домашнее задание на доске.