Цель урока: Научить проводить исследование функций; строить их графики.
Форма: урок-беседа.
Методы: диалог, наглядные пособия и слайды.
Оборудование: ИКТ, таблицы.
Ход урока
I. Проверка домашнего задания.
Учитель: - Ребята! У вас было домашнее задание "Критические точки функции, максимумы и минимумы". Дайте определение критической точки функции.
Ученик: - Критической точкой называется внутренняя точка области определения, в которой производная либо равна нулю, либо не существует.
Учитель: - Как найти критические точки?
Ученик: - 1
) Найти производную функции;
2) Решить уравнение: f '(x)=0. Корни этого уравнения являются критическими точками.
Учитель: - Найдите критические точки функций:
а) f(x)= 4 - 2x + 7x2
б) f(x)= 4x - x3/3
Ученик: -
а) 1) Найдем производную данной функции:
f '(x)= (4 - 2x + 7x2)' = -2+14x
2) Решим уравнение f '(x)=0 <=> -2+14x =0 <=> x=1/7
3) Так как уравнение f '(x)=0 имеет один корень, то данная функция имеет одну критическую точку х = 1/7.
Ученик: -
б) 1) Найдем производную данной функции: f '(x)= 4 - x2
2) Решим уравнение: f '(x)=0 <=> 4 - x2 = 0 <=> х = 2 или х = -2
3) Так как уравнение f '(x)=0 имеет два корня, то данная функция имеет две критические точки х1 = 2 и х2= -2 .
II. Устная работа.
Учитель: - Ребята! Повторим основные вопросы, которые нужны для изучения новой темы. Для этого рассмотрим таблицы с рисунками (приложение 1).
Укажите точки, в которых возрастание функции сменяется убыванием. Как называются эти точки?
Ученик: - На рисунке а) - точка К-это точка максимума, на рисунке б) - точка М - это точка максимума.
Учитель: - Назовите точки минимума функции.
Ученик: - Точка К на рисунке в) и г) - точка минимума функции.
Учитель: - Какие точки могут быть точками экстремума функции?
Ученик: - Критические точки могут быть точками экстремума функции.
Учитель: - Какие необходимые условия вы знаете?
Ученик: - Существует теорема Ферма. Необходимое условие экстремума: Если точка х0 является точкой экстремума функции f и в этой точке существует производная f ', то она равна нулю: f '(x)=0.
Учитель: - Найдите критические точки для функции:
а) f(x) = | х |
б) f(x) = 2х + | х |
Ученик: - Рассмотрим функцию f(x) = | х | (приложение 2). Эта функция не имеет производной в 0. Значит, 0- критическая точка. Очевидно, что в точке 0 функция имеет минимум.
Ученик: - Рассмотрим функцию f(x) = 2х + | х | (приложение 3). По графику видно, что в точке 0 эта функция не имеет экстремума. В этой точке функция не имеет и производной.
В самом деле, если предположить, что функция f имеет в точке 0 производную, то f(х) - 2х также имеет производную в 0. Но f(х) - 2х = | х |, а функция | х | в точке 0 не дифференцируема, т.е. мы пришли к противоречию.
Значит, функция f в точке 0 производной не имеет.
Учитель: - Из теоремы Ферма следует, что при нахождении точек экстремума нужно найти критические точки. Но из рассмотренных примеров видно, что для того чтобы данная критическая точка была точкой экстремума нужно еще какое-то дополнительное условие.
Какие достаточные условия существования экстремума в точке вы знаете?
Ученик: - Признак максимума функции: Если функция f непрерывна в точке х0 , а f '(x)>0 на интервале (а;х0) и f '(x) <0 на интервале (х0 ; в), то точка х0 является точкой максимума функции f.
То есть если в точке х0 производная меняет знак с плюса на минус, то х0 есть точка максимума.
Ученик: - Признак минимума: Если функция f непрерывна в точке х0 , а f '(x) <0 на интервале (а;х0) и f '(x) >0 на интервале (х0 ; в), то точка х0 является точкой минимума функции f.
То есть если в точке х0 производная меняет знак с минуса на плюс, то х0 есть точка минимума.
Учитель: - А какой алгоритм нахождения точек экстремума функции вы знаете.
Ученик объясняет алгоритм исследования функции f на экстремум с помощью производной (приложение 4) и находит точки экстремума функции:
f (х)= x4-2х2
D (f) =IR и f непрерывна на всей числовой прямой, как целая рациональная функция.
2. f '(x) = 4x3 -4х = 4х (х+1)(х-1).
3. f '(x)=0 <=> х= -1 V х=0 V х=1.

Рис.1 (знаки f ')
Так как f непрерывна в критических точках, то из рисунка 1 (приложение 5) видно, что -1 и 1 - точки минимума, а 0 - точка максимума функции f.
fmin = f (-1) = f (1) = -1, fmax = f (0) =0.
Учитель: - Ребята! Давайте вспомним алгоритм отыскания промежутков монотонности функции f.
Ученик вспоминает алгоритм отыскания промежутков монотонности функции f (приложение 6).
Учитель: - Найти промежутки возрастания и убывания функции f, заданной формулой
f (x)= x3-12х
Ученик:
- Решение:
1. Так как f(x) - многочлен, то D (f) =IR.
2. Функция f дифференцируема на всей числовой прямой и f '(x)= 3x2 -12 = 3 (х+2) (х-2).
3. Критическими точками функции f могут быть только нули f '(x).
f '(x) =0 <=> x = -2 V х=2.
D (f)\ {-2; 2}= (-![]() ; -2) U (-2 ; 2) U (2; +
; -2) U (-2 ; 2) U (2; +![]() ).
).
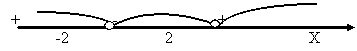
Рис.2 (знаки f ').
4. Посмотрев на рис.2 (приложение 7), записываем ответ:
f возрастает на (-![]() ; -2) и на (2; +
; -2) и на (2; + ![]() );
);
f убывает на (-2 ; 2).
Учитель: - Таким образом, мы с вами повторили алгоритм нахождения точек экстремума функции и алгоритм отыскания промежутков возрастания и убывания функции.
III. Объяснение нового материала.
Учитель: - Тема сегодняшнего урока: Примеры применения производной к исследованию функции.
На этом уроке мы должны научиться проводить исследование функций и строить их графики. Исследование функции на возрастание (убывание) и на экстремум удобно проводить с помощью производной. Для этого сначала находят производную функции f и ее критические точки, а затем выясняют, какие из них являются точками экстремума.
Для полного исследования функции f и построения ее графика удобно пользоваться общей схемой исследования, которая состоит из следующих пунктов (приложение 8):
Найти области определения и значений данной функции f.
Выяснить, обладает ли функция особенностями, облегчающими исследование, то есть является ли функция f:
а) четной или нечетной;
б) периодической.
3. Вычислить координаты точек пересечения графика с осями координат.
4. Найти промежутки знакопостоянства функции f.
5. Выяснить, на каких промежутках функция f возрастает, а на каких убывает.
6. Найти точки экстремума (максимум или минимум) и вычислить значения f в этих точках.
7. Исследовать поведение функции f в окрестности характерных точек не входящих в область определения.
8. Построить график функции.
Эта схема имеет примерный характер.
Учитывая все сказанное, исследуем функцию: f(x)= 3x5-5х3+2 и построим ее график.
Проведем исследование по указанной схеме:
D (f ') =IR, так как f (x) - многочлен.
Функция f не является ни четной, ни нечетной, так как
f (-x)= 3(-x)5-5(-x)3+2 = -3x 5+5х3+2= -(
3x5-5х3-2) ![]() f(x)
f(x)
Найдем координаты точек пересечения графика с осями координат:
а) с осью 0Х, для этого решим уравнение: 3x5-5х3+2 = 0.
Методом подбора можно найти один из корней (x = 1). Другие корни могут быть найдены только приближенно. Поэтому для данной функции остальные точки пересечения графика с осью абсцисс и промежутки знакопостоянства находить не будем.
б) с осью 0У: f(0)=2
Точка А (0; 2) - точка пересечения графика функции с осью 0У.
Отметили, что промежутки знакопостоянства не будем находить.
Найдем промежутки возрастания и убывания функции
а ) f '(x)= 15x4 -15х2 = 15х2 (х2-1)
D (f ') =IR, поэтому критических точек которых f '(x)не существует, нет.
б) f '(x) = 0, если х2(х2-1)=0 <=> x = -1 V x = 0 V x = 1.
в) Получим три критические точки, они разбивают координатную прямую на четыре промежутка. Определим знак производной на этих промежутках:

Рис.3 (знаки f ')
Из рисунка 3 (приложение 9)
видно, что: f возрастает на интервалах (-![]() ; -1) и
(1; +
; -1) и
(1; +![]() );
);
f убывает на (-1 ; 0) и (0; 1).
Так как функция непрерывна в точках -1; 0; 1, то f
возрастает на (-![]() ; -1] и [1; +
; -1] и [1; +![]() );
);
f убывает на [-1; 0] и [0; 1].
6. Найдем точки экстремума функции и вычислим значения функции в этих точках. Рассматривая рисунок 3 знаков f ?видим, что:
x =-1 - точка max, f (-1) =4;
x = 1 - точка min, f (1) =0.
Полученные результаты занесем в таблицу (приложение 10) и построим график (приложение 11).
IV. Закрепление новой темы. Решение задач.
Учитель: - Исследуйте функцию и постройте ее график: f (x)= x4-2х2-3.
Ученик: - 1) D (f) =R.
2) f(-x)= (-x)4-2(-x)2-3 = x 4-2х2-3; f(-x)= f(x),
значит, функция f является четной. Исследование
ее можно проводить на промежутке [0; ![]() ).
).
3) Найдем точки пересечения графика функции с
осями координат, то есть решим уравнение x 4-2х2-3
= 0. Пусть х2 =у, у2-2у-3= 0, у=3 или у=-1, то
есть х2=3, х=![]() 3
или х=-
3
или х=-![]() 3; х2=-1
не имеет решений. Получили две точки пересечения
с осью абсцисс М(
3; х2=-1
не имеет решений. Получили две точки пересечения
с осью абсцисс М(![]() 3;
0), К(-
3;
0), К(-![]() 3; 0). График
пересекает ось ординат в точке В (0; -3).
3; 0). График
пересекает ось ординат в точке В (0; -3).
4) Найдем производную f '(x) = 4x 3-4х = 4х(х-1)(х+1).
5) Найдем критические точки функции:
а) f ''(x) =0, если 4х (х-1) (х+1)=0, <=> x = 0 V x = -1 V x = 1.
б) f ' определена на всей D(f).
6) Определим знак производной на промежутках (-![]() ; -1),
(-1; 0), (0; 1), (1;
; -1),
(-1; 0), (0; 1), (1; ![]() ):
):
а) f '(2) = -32+8 < 0;
б) f '(-1/2) = 4 * (-1/2)3 -4 * (-1/2)= -1/2 + 2 > 0;
в) f '(1/2) = 4 * (1/2)3 -4 * (1/2)= 1/2 - 2 < 0;
г) f '(2) = 4 * 8 - 4 * 2 > 0.
Найдем значения функции в точках -1; 0; 1:
f (-1)=-4, f(0)=-3, f(1)=-4.
Полученные данные занесем в таблицу (приложение 12):
| x | (- |
-1 | (-1; 0) | 0 | (0; 1) | 1 | (1; |
| f ''(x) | - | 0 | + | 0 | - | 0 | + |
| f (x) | убывает | -4 | возрастает | -3 | убывает | -4 | возрастает |
| min | max | min |
Построим график (приложение 13).
Учитель: - Найти число корней уравнения: 2x 3-3x 2-12х-11=0
Решение: Рассмотрим функцию f(x)= 2x 3-3x 2-12х-11=0.
Найдем область определения функции: D (f) = (-![]() ;
; ![]() )
)
Найдем ее производную: f '(x) = 6x 2-6х-12
Найдем критические точки функции:
f '(x) =0, если 6x 2-6х-12=0, <=> x = -1 V x = 2.
Заполним таблицу (приложение 14):
| x | (- |
-1 | (-1; 2) | 2 | (2; |
| f ''(x) | + | 0 | - | 0 | + |
| f (x) | возрастает | -4 | убывает | -31 | возрастает |
| max | min |
5) а) На промежутке (-![]() ; -1] функция возрастает от
-
; -1] функция возрастает от
- ![]() до -4, поэтому на этом промежутке уравнение f (x)=0
корней не имеет.
до -4, поэтому на этом промежутке уравнение f (x)=0
корней не имеет.
б) На промежутке [-1; 2] уравнение так же не имеет корней, так как на этом промежутке функция убывает от -4 до -31.
в) На промежутке [2; ![]() ) функция возрастает от -31
до бесконечности, на этом промежутке уравнение f
(x)=0 имеет один корень (по теореме о корне, то есть
если функция возрастает (убывает) на промежутке I,
число а - любое из значений, принимаемых f на этом
промежутке, то уравнение f (x) = а имеет
единственный корень в промежутке I). Итак,
уравнение 2x 3-3x 2-12х-11=0 имеет один
корень и этот корень принадлежит интервалу (2;
) функция возрастает от -31
до бесконечности, на этом промежутке уравнение f
(x)=0 имеет один корень (по теореме о корне, то есть
если функция возрастает (убывает) на промежутке I,
число а - любое из значений, принимаемых f на этом
промежутке, то уравнение f (x) = а имеет
единственный корень в промежутке I). Итак,
уравнение 2x 3-3x 2-12х-11=0 имеет один
корень и этот корень принадлежит интервалу (2; ![]() ).
).
Учитель: - Сколько корней имеет уравнение: x 4/4 -x 3- x 2/2 +3х = 0
Ученик: - Решение: Рассмотрим функцию р(x) = x 4/4 -x 3- x 2/2 +3х:
1) Найдем область определения функции D(р) = (-![]() ;
; ![]() ).
).
2) Найдем производную р' (x) = x 3- 3x 2 -x+3
3) Найдем критические точки и промежутки возрастания и убывания функции:
р' (x) = 0 <=> x 3- 3x 2 -х+3=0 <=> x 2(х-3) -(х-3)=0 <=> (х-3)( x 2-1) = 0 <=> х=3, х1=1, х2=-1.

Рис. 4 (знаки р ')
Из рисунка 4 (приложение 15)
видно, что: р(x) возрастает на интервалах [-1; 1] и [3; +![]() );
);
р(x) убывает на (-![]() ; -1] и [1; 3].
; -1] и [1; 3].
4) Найдем точки экстремума и экстремумы функции:
х=-1 min р min= 1/4+1-1/2 -3=-9/4 < 0,
x= 1 max р max= 1/4 -1-1/2+3 =1 3/4 > 0,
х=3 min р min= 81/4-27-9/2+9= -27/2 < 0.
Строим эскиз графика (приложение 16).
Из рисунка видно, что многочлен имеет 4 корня, следовательно, уравнение имеет 4 решения.
V. Самостоятельная работа.
Вариант I.
Пример 1. Исследуйте функцию f(x)= x3-3х2 и постройте ее график
Решение:
Область определения данной функции - множество действительных чисел: D (f) =R.
Данная функция непрерывна на множестве действительных чисел как многочлен.
Найдем критические точки функции: f '(x)=3х2-6х = 3х (х-2),
f '(x)=0, 3х (х-2)=0, х=0 или х=2.
Составляем таблицу (приложение 17):
| х | (- |
0 | (0; 2) | 2 | (2; |
| f ''(х) | + | 0 | - | 0 | + |
| f (х) | возрастает | 0 | убывает | -4 | возрастает |
| max | min |
Критические точки разбивают координатную
прямую на три промежутка: (-![]() ; 0), (0; 2), (2;
; 0), (0; 2), (2; ![]() ).
).
![]()
Рис.5 (знаки f ')
На рисунке 5 (приложение 18) указаны знаки производной f '(x) на каждом из этих промежутков.
Найдем нули функции: x3-3х2 = 0, x2 (х-3) = 0, x = 0 или x = 3.
Найдем координаты еще одной точки графика: если x =-1, то f (-1) = (-1)3 - 3 * (-1)2 = -4.
6) Строим график данной функции (приложение 19).
Пример 2. Сколько корней имеет уравнение: x4 - 4x3 - 9 = 0.
Решение:
р (x) = x4 - 4x3 - 9
D(р) = (-![]() ;
; ![]() ).
).
р ' (x) = 4 x 3- 12x 2 = 4 x 2 (х-3) = 0, x1,2 = 0; x3 = 3
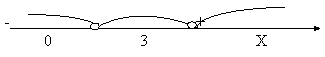
Рис.6 (знаки р ').
4) Из рисунка 6 (приложение 20)
видно, что: р(x) убывает на интервале (-![]() ; 3];
; 3];
р (x) возрастает на [3; +![]() ).
).
5) x = 3 - min
а) р min= р (3) = 34 - 4 * 33 - 9 = -36 < 0
б) в точке x = 0 график имеет точки перегиба (то есть меняет выпуклость), f (0) = -9.
6) Строим эскиз графика (приложение 21).
График пересекает ось 0Х в двух точках x1 и x2, следовательно, многочлен, а значит и данное уравнение имеет два корня.
Вариант II.
Пример 1. Исследуйте функцию y = 1/3x3- 3x2 + 8x и постройте ее график.
Решение:
Область определения данной функции - множество действительных чисел: D (y) =R.
Данная функция непрерывна на множестве действительных чисел .
Найдем критические точки функции: y ' = x2 - 6x + 8.
y ' = 0, x2 - 6x + 8 = 0, x = 2 или x = 4.
4) Составляем таблицу (приложение 22):
| х | (- |
2 | (2; 4) | 4 | (4; |
| y '' | + | 0 | - | 0 | + |
| y | возрастает | 20/3 | убывает | 16/3 | возрастает |
| max | min |
ymax = y(2) = 20/3, y min= y(4) = 16/3.
5) Найдем нули функции: 1/3x3- 3x2 + 8x =0, x (1/3x2- 3x + 8) = 0, x = 0 или 1/3x2- 3x + 8 = 0.
x2- 9x + 24 = 0, D = 92- 4 * 24 < 0, квадратное уравнение корней не имеет. Данная функция имеет только один нуль: x = 0. При x = 0 y = 0 - график функции проходит через начало координат.
6) Построим график функции (приложение 23).
Пример 2. Сколько корней имеет уравнение: x2- x3/3- 1= 0
Решение:
p (x) = -x3/3+ x2- 1.
D (p) = IR.
Исследуем функцию: p '(x) = -x2+ 2x = - x (x - 2) =0, x = 0 или x =2.
3) Найдем критические точки функции (приложение 24):
![]()
Рис.7 (знаки p')
x = 0 - min, p min= p (0) = -1 < 0;
x = 2 - max, p max= p (2) = - 8/3 + 4 - 1 = -8/3 +3 = 1/3 > 0.
4) Строим эскиз графика (приложение 25).
График пересекает ось 0Х в трех точках x1, x2 и x3, следовательно, многочлен, а значит и данное уравнение имеет три корня.
VI. Домашнее задание.
Выучить схему исследования функции.
Исследовать и построить график функции:
а) y = 3x4- 4x3 - 12x2 + 10;
б) y = ![]()
Спасибо, ребята. До свидания.