Цель: в результате изучения темы учащиеся должны знать понятие иррациональных уравнений, методы решения иррациональных уравнений, формировать умение решать иррациональные уравнения, применять их в практической деятельности.
Ход урока
I этап. Организационный момент.
II этап. Подготовка учащихся к сознательному усвоению знаний.
Учителем сообщаются задачи и цели урока: "На этом уроке познакомимся с еще одним видом уравнений - иррациональные уравнения. Рассмотрим различные методы решения. Тема эта актуальна, так как иррациональные уравнения часто встречаются на вступительных экзаменах в ВУЗы, с их помощью диагностируются ученики, начиная с понятия равносильности уравнений и заканчивая понятием ОДЗ".
"Перед вами стоит задача - прослушав лекцию, поработать с учебником, прорешать уравнения, показать знания и умения по решению иррациональных уравнений. За каждый этап урока будете получать баллы от 1 до 5. Суммировав их - соответствующую оценку. Желаю всем удачи!"
К доске вызываются двое учащихся с проверкой домашнего задания, а класс работает устно.
Вычислить: 1)![]() +
+![]() =
=![]() +
+![]() =
=![]() =
= ![]()
Ответ: 10.
2) ![]() .Подкоренные
выражения не являются полными квадратами, т. е.
применить приём из предыдущего примера не
удаётся. Возведём вычисляемое выражение в
квадрат:
.Подкоренные
выражения не являются полными квадратами, т. е.
применить приём из предыдущего примера не
удаётся. Возведём вычисляемое выражение в
квадрат:
(![]() )2=29-12
)2=29-12![]() -2
-2![]() 12
12![]() =
=
58-2![]() =58-22=36
=58-22=36
Следовательно, исходное выражение может быть равно 6 или -6; так как
![]() >
>![]() , то это
выражение отрицательно.
, то это
выражение отрицательно.
Ответ: -6.
Остальным учащимся предлагается вспомнить определение и основные свойства корня п-ой степени, ответить устно на вопрос: "Какие виды уравнений вы знаете?"
ах + в = 0 - линейное уравнение.
ax2+bx+c=0 - квадратное уравнение.
xn=a -простейшее степенное уравнение.
тригонометрические уравнения: sin![]() =a, cos
=a, cos![]() =a, tg
=a, tg![]() =a, ctg
=a, ctg![]() =a.
=a.
"Мы вспомнили эти уравнения, т.к. они актуальны при изучении новой темы".
III этап. Объяснение нового материала (лекция).
Мною предлагается лекция, в которой основной материал изложен одновременно в словесной, и знаково-символьной формах, главные вопросы которой, учащиеся должны запись в тетрадь.
Уравнения, в которых переменная содержится под знаком корня, называются иррациональными.
Решение иррациональных уравнений сводится к переходу от иррационального к рациональному уравнению путём возведения в степень обеих частей уравнения или замены переменной.
3. При возведении обеих частей уравнения в чётную степень возможно появление посторонних корней. Поэтому при использовании указанного метода следует проверить все найденные корни подстановкой в исходное уравнение.
Иногда удобнее решать иррациональные уравнения, определив область допустимых значений неизвестного и используя равносильные переходы.
Что значит решить иррациональные уравнения? Это значит: найти все такие значения переменной х, при которых уравнение превращается в верное равенство, либо доказать, что таких значений не существует.
Другие понятия для иррациональных уравнений определяются так же, как и для рациональных уравнений.
Широко распространенными иррациональными
уравнениями, предлагаемыми на вступительных
экзаменах, являются уравнения вида ![]() = В(х), где А(х) и В(х)
- алгебраические выражения, где неизвестная
величина содержится под знаком корня и уравнения
вида
= В(х), где А(х) и В(х)
- алгебраические выражения, где неизвестная
величина содержится под знаком корня и уравнения
вида ![]() .
.
Показывается способ решения уравнения данного вида:
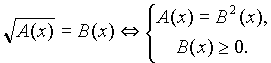 (1)
(1)
Примеры:
1) ![]() ;
;
2) ![]() = х - 2.
= х - 2.
Обратите внимательно на правые части уравнений. Во втором уравнении должно налагаться дополнительное условие, которое вытекает из определения арифметического корня n-ой степени.
Имеем ![]() = х
- 2. Пришли к системе
= х
- 2. Пришли к системе
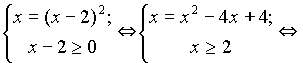 х2-
5х + 4 = 0
х2-
5х + 4 = 0
х1 = 4,
х2 = 1- посторонний корень, не удовлетворяет условию х ? 2.
Еще один вид иррационального уравнения ![]() сводится к
системе
сводится к
системе
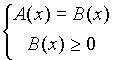 (2)
(2)
Кстати, можно проверять и А(х)? 0, т.е. то, что в данной задаче проще. Если уравнение не относится ни к одному из видов, то с помощью различных преобразований можно привести уравнения к I или II виду.
Основные методы решения иррациональных уравнений:
I. Уединение радикала и возведение в степень.
II. Метод введения вспомогательного неизвестного или "метод замены".
III. Уравнения, содержащие кубические радикалы.
IV. "Искусство" или нестандартный подход.
Обобщим изложенное по новой теме:
Определение иррациональных уравнений.
Два вида иррациональных уравнений.
Четыре метода решения.
Чаще встречаются два метода - "Уединение радикала и возведение в степень" и "Введение новой переменной".
Решим уравнения.
а) ![]() = х.
= х.
Решение
Возведём обе части уравнения в квадрат:
х+2=х2,
х2-х-2=0,
х, = -1, х2=2.
Проверка: 1)x=-1, тогда![]() -1,1=-1-ложно;
-1,1=-1-ложно;
2) x=2, тогда ![]() =2,2=2
верно.
=2,2=2
верно.
Ответ: x=2
б) ![]() +1-2x=0.
+1-2x=0.
Решение:
![]() =2x-1,
=2x-1,
x2+5x+1=(2x-1)2,
x2+5x+1=4x2-4x+1,
x(x-3)=0,
x1=0, x2=3.
Проверка:
x1=0,то ![]() +1-2*0
+1-2*0![]() 0, значит,x1=0 не
удовлетворяет уравнению.
0, значит,x1=0 не
удовлетворяет уравнению.
x2=3, тогда ![]() +1-2*3=0. Значит, x=3- корень уравнения.
+1-2*3=0. Значит, x=3- корень уравнения.
Ответ: 3;
в)![]()
Решение
Возведя обе части уравнения в квадрат, получим 2х-3 =х -2, х = 1.
Проверка:![]() .
Обе части уравнения не имеют смысла.
.
Обе части уравнения не имеют смысла.
Ответ: нет корней;
г) решить уравнение ![]() +
+![]()
Решение:
![]() . Поскольку
корни арифметические, то левая часть уравнения
неотрицательна, а правая отрицательна, значит,
уравнение решений не имеет.
. Поскольку
корни арифметические, то левая часть уравнения
неотрицательна, а правая отрицательна, значит,
уравнение решений не имеет.
Ответ: уравнение решений не имеет;
д) решить уравнение ![]() =6.
=6.
Решение:
Область допустимых значений неизвестного (ОДЗ)
этого уравнения определяется системой
неравенств,![]()
![]() ,которая решений
не имеет. Уравнение не определено в множестве
действительных чисел. Ответ: уравнение решений
не имеет;
,которая решений
не имеет. Уравнение не определено в множестве
действительных чисел. Ответ: уравнение решений
не имеет;
е) решить уравнение ![]() =х-8.
=х-8.
Решение:
По определению квадратного корня уравнение ![]() = х-8 равносильно
= х-8 равносильно
системе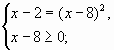
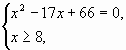
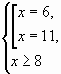 x=11
x=11
Ответ:11.
IV этап. Первичная проверка понимания.
Учащиеся решают самостоятельно в группах, затем обсуждают свое решение. Отвечают на вопросы учителя о том, сколько корней имеет уравнение, почему столько, отчего это зависит, как нужно находить О.Д.З., нужно ли проверять корни и другие. Затем сверяют своё решение с решением сильного ученика на переносной доске (сначала они не видят, как он решает).
Решить №417(а) ![]() ;
;
Решить №418(а; б) а)![]() ; б)
; б)![]()
Решить № 419 (а; г) а)![]() ,
,
г)![]() .
.
Группе ребят, которая первой закончила выполнение задания верно, обсудив решения между собой, ответив на дополнительные вопросы учителя, выставляются отметки за работу на уроке.
Итоги урока.
Хочется закончить урок словами китайской пословицы:
"Расскажи - и я забуду, покажи - и я запомню, дай попробовать - и я пойму". Я надеюсь, что с иррациональными уравнениями на ЕГЭ у вас не будет никаких трудностей! Мы сегодня решали иррациональные уравнения несколькими способами, но это не все. Дома найдите еще. И найдите дома не из учебника любые иррациональные уравнения, которые мы здесь решим.
Домашнее задание:
п. 33 (до примера 6);
1 группа: решить № 417(в), № 418(в; г), (приложение 2)
2 группа: решить № 419(б; в), №422 (а; г),
3 группа: решить № 425(б), из ЕГЭ ![]() =
=![]() (приложение 3)
(приложение 3)
Решить по одному примеру из пяти тем к концу прохождения модуля, т.е. принести решения пяти номеров через три урока. Ваш вариант соответствует номеру вашей фамилии в журнале. Смотри приложение 1.