Решение неравенств второй степени с одной переменной. Урок-семинар по математике. 9-й класс

Цели:

- обобщить и систематизировать знания учащихся по теме;

- отработать основные методы и способы решения неравенств;

- уметь применять знания при решении нестандартных задач;

- развивать математическую речь, умение выступать с самостоятельными сообщениями, логически излагать мысль;

- воспитывать интерес к математике, стремление глубже усвоить материал.

 Тип урока: обобщение и углубление пройденного материала.

 Оборудование: доска, презентация “Решение неравенств” (Приложение 1).

 ХОД УРОКА

І. Оргмомент: объявляется тема урока, цели, учащиеся знакомятся с планом семинара (слайд 2).

План.

1. Неравенства (историческая справка).
2. Неравенства ІІ степени. Схема решения. Примеры решения.
3. Метод интервалов (схема).
4. Решение неравенств методом интервалов.
5. Применение умения решать неравенства в нестандартных задачах.

 ІІ. 1. Неравенства (историческая справка).

Cообщение, подготовленное учеником (слайд 3, 4).

“Неравенство – соотношение между числами и величинами, указывающее, какие из них больше других. Неравенства обладают многими свойствами, общими с равенствами. Так Н. остаётся справедливым, если к обеим частям его прибавить или отнять одно и то же число. Точно также можно умножить обе части Н. на одно и то же положительное число. Однако, если обе части Н. умножить на отрицательное число, то смысл Н. изменится на обратный. Н. , в которые входят величины, принимающие различные числовые значения, могут быть верны для одних значений этих величин и неверны для других. Существуют наиболее важные типы Н.:

1) неравенство для модулей. Для любых действительных или комплексных чисел а₁, а₂, …, а_n справедливо Н. |а₁+а₂+…+а_n| ≤|а₁|+|а₂|+…+|а_n|.

2) неравенство для средних. Наиболее известны Н., связывающие гармонические, геометрические, арифметические и квадратичные средние:

п⁄(1⁄а₁+1⁄а₂+…+1⁄а_n)≤ⁿ√а₁.а₂…а_n ≤(а₁+а₂+…+а_n)⁄n≤√(а₁²+а₂²+…+а_n²)⁄n.

Здесь все числа а₁ ,а₂ ,…,а _n - положительны.

3) неравенства для билинейных и квадратичных форм.

4) неравенства для некоторых классов последовательностей и функций. Например, неравенства Чебышева для монотонных последовательностей.

5) неравенства для определителей.

Неравенства имеют существенное значение для всех разделов математики. В теории чисел целый раздел, диофантовы приближения, полностью основан на Н.. Аналитическая теория чисел тоже часто оперирует с Н. В геометрии Н. постоянно встречаются в теории выпуклых тел. В теории вероятностей многие законы формулируются с помощью Н.. В теории дифференциальных уравнений используются так называемые дифференциальные Н. Неравенства приобрели первостепенное значение в математике после того, как в результате работ немецкого математика К. Гаусса, французского математика О.Коши, русского математика П.Л. Чебышева была поднята до теоретической высоты роль приближённых методов.

В настоящее время, всюду, где рассматриваются экстремальные задачи, приближённые решения, оценки или асимптотические формулы, появляются Н. Многие классические Н. постоянно употребляются в различных исследованиях. Нередки такие случаи, когда конечный результат какого-либо исследования выражается в форме Н.”

2. Неравенства ІІ степени. Схема решения. Примеры решения.

У - “Какие неравенства называются неравенствами ІІ степени и как они решаются, познакомит нас следующий выступающий” (слайд 5).

“Неравенства вида ах²+вх+с>0 и ах²+вх+с<0, где х - переменная, а, в, с - некоторые числа, причём а≠0, называют неравенствами второй степени с одной переменной.

При решении Н. мы используем свойства квадратичной функции (нахождение промежутков, где функция принимает положительные или отрицательные значения).

 Схема

Рассмотрим функцию у=ах²+вх+с.

1. Определим направление ветвей параболы.
2. Определим расположение параболы относительно оси абсцисс.
3. Покажем схематически расположение параболы в координатной плоскости.
4. Из графика находим промежутки, где у>0 (у<0).
5. Ответ.

Пример: решить неравенство 3х²+4х-4>0 (слайд 6).

Решение. Рассмотрим функцию у=3х²+4х-4.

1. а=3>0, ветви направлены вверх.

2. 3х²+4х-4=0, Д₁=2²-3·(-4)=16, 16>0, х=(-2±4)/3; х₁=-2, х₂=2/3.

3.

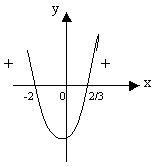
4. у>0 при хє(-∞;-2)υ(2/3;+∞).

Ответ: (-∞;-2)υ(2/3;+∞)”.

У: Задание классу: решите неравенство 2х²+8х-111<(3х-5)(2х+6).

(На оборотной стороне доски решает ученик, остальные в тетрадях, затем решение проверяется).

 Решение: 2х²+8х–111<6х²+8х–30, –4х²–81<0, 4х²+81>0.

Рассмотрим функцию у=4х²+81, 1) а=4>0, ветви направлены вверх,

2) 4х²+81=0, х²=–81/4, корней нет, с осью абсцисс график не пересекается,

3) схематический рисунок,

4) у>0 при любых х,

5) ответ: (-∞; +∞).

3. Метод интервалов (схема).

У. - “В чём суть метода интервалов - нам расскажет следующий ученик” (слайд 7, 8).

“Пусть функция задана формулой f(х)=(х-х₁)(х-х₂)…(х-х_n), где х - переменная, а

х₁, х₂, …,х _n - нули функции. В каждом из промежутков, на которые область определения разбивается нулями функции, знак функции сохраняется, а при переходе через нуль её знак изменяется. Это свойство используется при решении неравенств.

Например, х(х+5)(2-х)>0.

 Решение:

1) Рассмотрим функцию у=х(х+5)(2-х).

2) нули: х=0, х=-5, х=2.

3) Определим знак функции на каждом из промежутков. Для этого найдём знак функции на крайнем правом промежутке (2;+∞). При х=3 значение функции

у=х(х+5)(2-х)<0. Далее используем свойство чередования знаков функции. Получим:

4) Ответ: (-∞; -5) υ ( 0; 2).

4. Решение неравенств методом интервалов.

№ 198(г), 202(б, г) (двое учащихся решают с тыльной стороны доски, затем решения объясняют)

№198(г). Решите неравенство: х^3–0,01х>0.

Решение: х(х²-0,01)>0, х(х-0,1)(х+0,1)>0, нули: х=0, х=0,1, х=–1,

Ответ: (-0,1;0)υ(0,1;∞).

№ 202(б). Решите неравенство: (х+16)⁄(х-11)<0.

Решение: Знак дроби совпадает со знаком произведения, поэтому неравенство равносильно неравенству (х-16)(х-11)<0, нули: х=16, х=11;

Ответ: (11;16)

(г). (6-х)⁄(х-4)≤0.

Решение: Знак дроби совпадает со знаком произведения, а область определения дроби не содержит х=4, поэтому данное неравенство равносильно системе неравенств

(6-х)(х-4)≤0,  х≠4;
х=6, х=4,  х≠4.

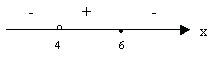
Ответ: (-∞;4)υ 6;+∞).

5. Применение умения решать неравенства в нестандартных случаях.

№191(а). Найти область определения функции: у=1⁄√144–9х².

 Решение: по определению квадратного корня 144–9х²≥0, и поскольку делить на нуль нельзя, то 144–9х²>0; (12–3х)(12+3х)>0, нули: х=4, х=-4.

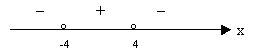
Ответ: (-4;4).

№ 199*(в). Решите неравенство: (х-1)² (х-24)<0 .

Решение: рассмотрим функцию у=(х–1)² (х–24). Нули: х=1, х=24. Нуль 1 –кратный. Наличие кратных корней не позволяет пользоваться свойством чередования знаков функции, поэтому надо определять знаки функции на каждом промежутке.

у(0)=1·(–24)=–24, –24<0,

у(2)=1·(–22)=–22, –22<0,

у(25)=24²·1=576, 576>0.

 ІІІ. Итоги урока.

1. Сколькими способами мы научились решать неравенства.
2. Решать неравенства второй степени мы можем по предложенной схеме, используя свойства квадратичной функции (промежутки знакопостоянства). При решении других неравенств, третьей и выше степеней, пользуются методом интервалов, который основан на свойстве чередования знаков функции на промежутках (если функцию можно представить в виде произведения линейных множителей, в противном случае, определяют знак функции на каждом промежутке отдельно). Такая работа нам предстоит в десятом классе.
3. Всем, выступившим ученикам и, работавшим у доски, выставляются оценки.

 ІV. Домашнее задание: №199 г, 114б.