Развитие компонентов математической деятельности учащихся на уроках математики

Разделы: Математика

В настоящее время общество для своего полноценного функционирования нуждается в таких своих представителях, которые умеют хорошо ориентироваться в информационных ресурсах из различных областей знаний, применять эти знания в новых, измененных условиях, разрешать противоречия, предлагать нестандартные решения проблемных ситуаций в социальном взаимодействии с другими субъектами общества. Все это не может не отразиться на увеличении объема требований, которые предъявляются к организации школьного обучения на современном этапе развития общества.

Каждый учебный предмет, изучаемый в общеобразовательной школе, имеет возможности для повышения уровня развития интеллекта, способностей учащихся. Школьный курс математики не является исключением. Его структура и содержание предоставляют большие возможности для развития интеллектуальных и личностных качеств учащихся.

Одним из конкретных путей решения вышеперечисленных задач является такая организация учебного процесса, которая обеспечивала бы условия для развития интуитивных, логических и творческих компонентов математической деятельности учащихся, как по отдельности, так и в совокупности, что, в свою очередь, положительным образом влияет на развитие интуиции, логического мышления, творческого мышления учащихся. Все это в сочетании способствует развитию математических способностей и, как следствие, повышению качества их математической подготовки.

Говоря о математической деятельности ученика, мы имеем ввиду не только обучаемость, но и учебную деятельность, в процессе реализации которой учащиеся, самостоятельно или в сотрудничестве с другими субъектами учебного процесса, творчески овладевают математическим содержанием в условиях школьного обучения. Творческое познание и преобразование математических объектов, в большинстве случаев, носит субъективный характер. Связано это с тем, что к математической деятельности, во всей полноте проявления содержания этого понятия, ученик не способен, но когда он, действуя в специально организованной педагогической ситуации, открывает теорему или ищет новый способ решения задачи, он воспроизводит действия, характеризующие математическую деятельность на субъективном уровне, что способствует повышению продуктивности результатов учебной деятельности учащихся.

Под соответствующими компонентами математической деятельности (КМД) учащихся целесообразно понимать действия, в реализации которых в наибольшей степени проявляются качества определенного типа мышления, и которые наиболее интенсивно могут развиваться у учащихся в процессе обучения их математике.

Учитывая особенности содержания школьного курса математики, можно утверждать, что в процессе его изучения учащиеся должны приобрести умения:

  • четко и правильно излагать свои мысли; проводить последовательные и логически обоснованные рассуждения; формулировать закономерности; выделять и планировать последовательность (этапы) выполнения определенной деятельности (составлять алгоритм) [логические КМД].
  • выдвигать предположения; предвидеть пути развития некоторых событий или последствий принятых решений; рассуждать по аналогии; обобщать результаты, полученные для частного случая на все множество объектов определенного класса [интуитивные КМД].
  • рассматривать разнообразные решения одной и той же проблемы (варьировать способы действий); переходить от одного способа действия к другому, в случае его неэффективности; переносить свойства одного объекта на другой; рассматривать две или более противоположностей одновременно; преобразовывать полученное знание, то есть делать его более оригинальным, доступным, не искажая при этом его первоначальный смысл [творческие КМД] [1- 6].

Развитие перечисленных КМД учащихся в той или иной мере можно осуществить в процессе решения задач соответствующего содержания.

Интуитивные КМД в наибольшей степени проявляются, например, в процессе решения следующих задач:

  1. Выскажите свои предположения относительно выражения, по которому можно вычислить площадь фигуры, ограниченной графиками функций у=х2-1 и у=х3 и прямой х=1. Какие изменения произойдут, если функцию у=х3 заменить на у=0,5х3 и убрать х=1.(чертеж выполняется только после того, как учащиеся выскажут свое мнение).
  2. Дан цилиндр. Его высоту увеличили в 2 раза, радиус основания уменьшили в 2 раза. Какие последствия могут иметь данные изменения?
  3. Дан цилиндр объема-Х. С цилиндром произвели ряд действий, в результате которых объем увеличился в 8 раз. Какие действия могли привести к подобным результатам?
  4. Определите как можно больше различий между функциями y=sinx и y=cosx. Найдите между ними как можно больше общих свойств и т.п.

Развитию логических КМД способствуют задачи следующего содержания:

  1. Докажите, что функция у=2х является возрастающей.
  2. Дано: у=3х+2. Какие следствия можно вывести?
  3. ДАВС – правильный тетраэдр. М – середина ребра АС. Выведите следствия.
  4. Выделите условия, которые необходимо проверить при использовании признака параллельности двух плоскостей.
  5. Составьте алгоритм для нахождения производной сложной функции.
  6. Найдите и исправьте ошибки. Объясните их:
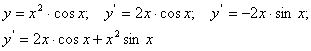
  7. Выделите существенные свойства усеченной пирамиды.
  8. Выделите главное при изучении прямоугольного параллелепипеда.
  9. На что необходимо обратить особое внимание при решении уравнений:
    1) t=cosx.
    2) 4x=a.
  10. Выделите общие свойства показательной и логарифмической функций.
  11. Чем различаются прямоугольный параллелепипед и куб? и т.п.

Творческие КМД могут быть реализованы в процессе решения следующих задач:

  1. Сформулируйте по – новому определение точек экстремума, не исказив при этом смысл понятия.
  2. Выделите свойства цилиндра, которые можно применить к конусу.
  3. Установите связь конуса с цилиндром, пирамидой, противопоставив их свойства.
  4. Решите уравнение: 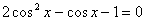. Измените содержание задания так, чтобы оно:
    1) имело ограниченное число корней;
    2) не имело корней…и т.п.

Необходимо отметить, что проявление соответствующих КМД учащихся в процессе решения задач определенного содержания носит субъективный характер, так как все зависит от опыта учащихся в решении подобных задач, от уровня их сложности.

С целью повышения качества знаний учащихся по математике процесс их обучения должен быть направлен на комплексное развитие указанных КМД учащихся. Это означает, что совместная деятельность учителя и учащихся должна подразумевать определенные этапы. На подготовительном этапе учитель после актуализации опорных знаний учащихся демонстрирует им учебное задание. Учащиеся, проанализировав его содержание, должны высказать предположения относительно способов его решения. Предположения фиксируются с целью последующей проверки, которая осуществляется с помощью соответствующих средств под руководством учителя. На основании полученных результатов делаются общие выводы, полученные знания применяются к решению задач.

Таким образом, учащиеся в процессе изучения содержания школьного курса математики последовательно переходят от интуитивных, собственных представлений об изучаемых объектах, своих предположений к логически обоснованным доказательствам или опровержениям этих предположений и представлений, а от этого к творческому преобразованию объекта, поиску его связей с ранее изученным материалом.

Рассмотрим конкретные примеры.

  1. В процессе изучения темы «Преобразование графиков тригонометрических функций» учитель предлагает учащимся высказать предположения о возможных преобразованиях графиков следующих функций:
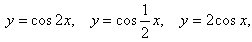
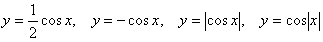
    После того как предположения будут зафиксированы осуществляется их проверка. Для этого учащиеся должны построить графики функций и сделать соответствующие выводы.
    По итогам работы учитель предлагает учащимся обобщить результаты, составить и решить аналогичные задания для остальных тригонометрических функций (возможна групповая работа).
  2. Постройте график функции  Изучите полученные результаты и сформулируйте как можно больше свойств для указанной функции. Выскажите предположения относительно возможных преобразованиях графика функции, которые не изменят промежутки монотонности исходной функции (изменят характер монотонности функции на противоположный на соответствующих промежутках). Представьте конкретные примеры возможных преобразований.
  3. Рассмотрите различные изображения прямого кругового цилиндра (объекты демонстрируются учителем). Выскажите предположения относительно его свойств, которые вы наблюдаете или о которых догадываетесь. Проверьте свои предположения. Определите практические способы построения прямого кругового цилиндра.
  4. Перед изучением теоремы, выражающей связь между знаком производной на отрезке и монотонностью функции на этом отрезке, учащимся может быть предложено задание:
    «1) Постройте графики функции:
    а) у = 3х2 + 1; б) у = 4х2+ 4х +1; в) у = - 2х3 – 2х.
    2) Вычислите производные данных функций и найдите нули полученных производных.
    3) Отметьте нули производной на координатной прямой и оцените знак производной на каждом из получившихся промежутков.
    4) Сравните полученные результаты с построенными графиками. Сделайте вывод».
    Учащиеся могут достаточно быстро выполнить предложенное задание с помощью специальной компьютерной программы и «открыть» теорему: «Если функция непрерывна на некотором промежутке и ее производная неотрицательна (неположительна) на этом промежутке и равна нулю лишь в конечном числе точек, то функция возрастает (убывает) на данном промежутке».

Все это очень важно для развития КМД учащихся, так как при такой организации изучения материала они проходят путь поиска нового знания: они выдвигают гипотезы, проверяют их сначала на частных случаях, затем доказывают, а после этого обобщают свои выводы.

Нельзя не упомянуть о таком приеме как экспериментирование, который предоставляет немалые возможности для комплексного проявления и развития КМД учащихся. В наибольшей степени данный прием может быть реализован в процессе использования таких форм обучения как практические и лабораторные работы.

Например, учащимся после изучения свойств цилиндра, конуса и шара (при совместном их изучении) может быть предложена лабораторная работа по исследованию возможных вариантов сечений данных геометрических тел и выводу формул для вычисления площадей полученных сечений. Конечно, не для всех сечений учащиеся смогут найти формулы для вычисления площади, но они могут предложить свои варианты, которые преподаватель впоследствии может уточнить.

Учащиеся для того, чтобы выполнить поставленные перед ними задачи должны исследовать разные варианты решения, проявить навыки творческого поиска и др. К сожалению, в рамках традиционного урока математики подобные формы работы реализовать достаточно проблематично, в большинстве случаев из – за временных ограничений. Но использование компьютера и специальных учебных программ может помочь с успехом преодолеть эти трудности.

Таким образом, вовлекая учащихся в процесс открытия, преобразования математических объектов, учитель создает благоприятные условия для развития у них положительной мотивации к процессу изучения математики, повышения качества их знаний, и, что особенно важно, для комплексного развития интуитивных, логических и творческих компонентов математической деятельности учащихся.

Список литературы:

  1. Богоявленская Д.Б. Психология творческих способностей. – М.: Издат. Центр «Академия», 2002. – 320 с.
  2. Бондаренко Л.И. У истоков логического мышления. – М.: Знание, 1985 . – 64 с.
  3. Дружинин В.Н. Психология общих способностей. – СПб.: Изд – во Питер, 2000. – 368 с.
  4. Зинченко В.П. Психологические основы педагогики. – М.: Гардарики, 2002. – 431 с.
  5. Крутецкий В.А. Психология математических способностей школьников. – М.: Изд – во «Институт практической психологии», Воронеж: Изд – во НПО «МОДЭК», 1998. – 416 с.
  6. Спиридонов В.Ф. Психология мышления: Решение задач и проблем. – М.: Генезис, 2006. – 319 с.