Предисловие
Многолетняя практика экзаменов по математике стимулировала создание мощного производства по “изготовлению” задач, в частности уравнений.
На вступительных экзаменах, в вариантах ЕГЭ, централизованного тестирования все чаще предлагаются уравнения с разными функциями: степенными, показательными, логарифмическими, тригонометрическими, так называемые комбинированные уравнения.
Учащиеся, владеющие только стандартными методами решения уравнений, как правило, попадают в расставляемые экзаменаторами ловушки. “Берясь” за решение уравнения, они концентрируют свое внимание только на поиске преобразований, сводящих исходное уравнение к более простому, забывая при этом, что упрощение полезно и возможно не всегда.
Далее речь пойдет о наиболее общих методах, используемых при решении комбинированных уравнений.
1. Метод разложения на множители. Метод введения новой переменной.
Сначала рассмотрим несколько несложных уравнений, иллюстрирующих наиболее распространенную схему решения.
Пример 1.1 Решить уравнение:
![]()
Решение:
ОДЗ: x I (-0,5; 0,5)
Используем формулу перехода к новому основанию логарифма и выносим за скобку общий множитель.

 U
U  U
U ![]()
Выполним отбор корней, учитывая ОДЗ.
 U
U  U k I ? , следовательно,
U k I ? , следовательно,
уравнение не имеет корней.
Ответ: корней нет.
Пример 1.2. Решить уравнение:
![]() .
.
Решение:
ОДЗ: ![]()
Переходя к основанию (x +1) и преобразуя логарифм степени, имеем
![]()
Разделим обе части уравнения на ![]()
6![]() - 13
- 13![]() + 6 = 0
+ 6 = 0
Пусть ![]() = t,
тогда имеем
= t,
тогда имеем
6t2 -13t + 6 =0, t> 0
Решая квадратное уравнение, находим ![]() ,
, ![]()
Возвращаясь к прежней переменной, получим совокупность
 U
U 
Учитывая ОДЗ, имеем x = ![]() .
.
Ответ: x = ![]() .
.
2. Использование экстремальных свойств функции. Метод оценок.
Обоснованием метода оценок является
Теорема №1: “Если на промежутке Х
наибольшее значение функции ![]() равно A и наименьшее
значение функции y = g(x) тоже равно A , то
уравнение
равно A и наименьшее
значение функции y = g(x) тоже равно A , то
уравнение ![]() = g(x)
равносильно системе уравнений
= g(x)
равносильно системе уравнений ![]()
Применение метода оценок предполагает нахождение наибольшего и наименьшего значений элементарных функций или их “композиций” на заданном множестве, а также использование некоторых “полезных” неравенств:
1. Неравенство Коши. Пусть ![]()
Тогда имеет место ![]() где k
где k![]() 2
2
В частности, если k =2, то неравенство Коши принимает вид:
![]() , где
, где ![]() (1)
(1)
2. Неравенство для суммы двух взаимно обратных
чисел ![]() где а >
0, (2)
где а >
0, (2)
которое также является следствием неравенства
(1), если допустить, что ![]() .
.
3. Неравенство для разности двух взаимообратных
чисел ![]() , где а<
0. (3)
, где а<
0. (3)
4. Неравенство а2 + в2 ![]() 2/ав/. (4)
2/ав/. (4)
5. Неравенство для суммы синуса и косинуса одного и того же аргумента:
![]() (5)
(5)
Пример 2.1. Решить уравнение:
![]() .
.
Решение:
О.Д.З.: x - любое, кроме ![]()

![]()
![]() по свойству
(2).
по свойству
(2).

![]()

Корень показательного уравнения ![]() является также корнем
тригонометрического уравнения системы
(проверяем подстановкой), следовательно,
является также корнем
тригонометрического уравнения системы
(проверяем подстановкой), следовательно, ![]() - решение системы
и корень исходного уравнения.
- решение системы
и корень исходного уравнения.
Ответ: ![]() .
.
3. Использование свойства монотонности функций.
Для решения комбинированных уравнений с использованием монотонности функций полезно знать следующую теорему:
Теорема № 2. Если функция ![]() - возрастающая на
- возрастающая на ![]() , функция
, функция ![]() - убывающая на
- убывающая на ![]() , то уравнение
, то уравнение ![]() либо не имеет
корней, либо имеет единственный корень на
либо не имеет
корней, либо имеет единственный корень на ![]() .
.
Пример 3.1. Решить уравнение:
![]()
Решение:
О.Д.З.: ![]() .
.
Выполнив преобразования, получим
![]() ,
,
![]() ,
,
![]() .
.
Очевидно, что x = 7 - корень уравнения. Докажем, что других корней нет.
Функция ![]() -
убывает на
-
убывает на ![]() .
.
![]() ,
,
![]()
Если ![]() , то
, то ![]() , следовательно
, следовательно ![]() возрастает на
возрастает на ![]() , тогда по теореме
2 уравнение
, тогда по теореме
2 уравнение ![]() имеет единственный корень.
имеет единственный корень.
Ответ: 7.
Примечание
Методы, рассмотренные в §2; §3 представляют собой две разновидности функционально-графического метода.
4. Применение производной.
Нахождение области значений элементарных функций, входящих в комбинированное уравнение, не всегда возможно осуществить, используя свойство ограниченности их области значений. В таких случаях бывает полезно применить производную для нахождения экстремумов функций.
Пример 4.1. Решить уравнение:
![]()
Решение:
![]()
Пусть ![]() ;
; ![]() .
.
Найдем ![]() -
области значений этих функций.
-
области значений этих функций.
![]() , т.к. графиком
функции
, т.к. графиком
функции ![]() является парабола с направленными вниз
является парабола с направленными вниз
ветвями и вершиной в точке (0;1).
![]()
![]()
x = 0 - критическая точка функции ![]()
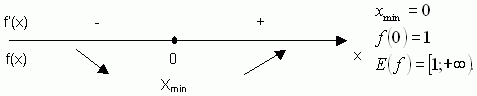
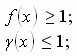
равенство ![]() возможно, если
возможно, если

Корень второго уравнения x = 0 подставим в первое уравнение системы, получим верное числовое равенство, следовательно x = 0 - решение системы и корень исходного уравнения.
Ответ: 0.