“Развивать творческие возможности
ученика
можно, только непосредственно включая его
в творческую деятельность через систему
познавательных задач поискового характера”.
академик А.И. Маркушевич
Математический бой – командное соревнование по решению математических задач, которое проводится между двумя командами учащихся одного класса. В ходе подготовки к такому бою ученикам предлагаются задачи (10 – 20 в зависимости от темы и уровня сложности задач). На решение задач отводится две недели. Учащиеся знают, что оценка команды зависит от оригинальности метода решения, наличия различных способов, поэтому решает задачи вся команда. Учитель до проведения боя может посмотреть решения каждой команды (не помогая и не комментируя).
В день проведения математического боя, как правило, после уроков в кабинете математики собираются обе команды, жюри, состоящее из учителей математики школы, болельщики. Право первого хода разыгрывается между капитанами команд решением какой-нибудь задачи на смекалку. Каждая задача математического боя имеет свою “цену”, о которой участники знают заранее и поэтому капитаны вправе выбрать наиболее сложные задачи, за правильное решение которых команда получит больше очков. В ходе боя капитаны руководят членами команд, определяют, кто и какую задачу представляет на доске (чертежи должны быть выполнены заранее на плакатах участниками боя). Решение ученика слушают все. Противники при этом предельно внимательны, потому что по правилам математического боя им предстоит найти пробелы в изложении, задать “хитрые” вопросы, призванные проверить глубину понимания задачи; предложить другое решение, если оно есть. Работа каждого ученика оценивается жюри. Учитель участвует в проверке решения, корректирует его в случае необходимости. Команды представляют задачи по очереди. Жюри само решает, по какой системе оценивать решения (исходя из первоначальной “стоимости” задачи), дополнения, заданные вопросы. Побеждает команда, набравшая наибольшее количество очков.
Такая работа позволяет ощутить красоту математики, научиться азам работы над задачами.
Предлагаю Вашему вниманию задания для учащихся 10-го класса по теме “Задачи с параметрами”.
- Определите, при каких значениях параметра а, уравнение (a2 – 9) cos x = a + 3 имеет решения. (Решение: см. приложение №1)
- Определите, при каких значениях параметра а, уравнение
- Определите, при каких значениях параметра а,
уравнение
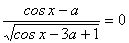 имеет
решения.
имеет
решения. - Определите, при каких значениях параметра а,
уравнение
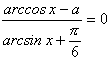 имеет решения.
имеет решения. - Определите, при каких значениях параметра а, уравнение
- Решите уравнение
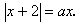 в зависимости от значений параметра а:
в зависимости от значений параметра а: - Решите уравнение
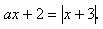 в зависимости от значений параметра а:
в зависимости от значений параметра а: - При каких значениях параметра а, число –1 лежит между корнями уравнения х2 + 2(а + 1) х + 4а + 4 = 0?
- Найдите все значения параметра а, при которых оба корня уравнения х2 – 2ах + а2 – 1 = 0 удовлетворяют неравенству –2 < х < 4.
- При каком значении параметра а, система
уравнений:
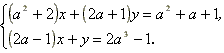
а) имеет единственное решение; б) не имеет решений; в) имеет бесчисленное множество решений? - Найдите все значения параметра а, для
каждого из которых неравенство выполняется для
любых чисел х и y таких, что
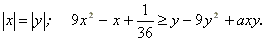
- При каком значении а касательная к графику функции y = а – х2 отсекает от первой четверти равнобедренный прямоугольный треугольник с площадью, равной 9/32?
- Пусть квадратное уравнение (а – 2)х2 – 2(а + 3)х + 4а = 0 имеет корни х 1 и х2. Найдите все такие а, что х1 и х2 удовлетворяют неравенству: х1 < 2 < 3 < х 2.
- При каких действительных значениях параметра а,
существует хотя бы одно действительное х,
удовлетворяющее условиям:
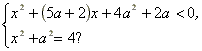
- Найдите все числа p, при которых
существует единственное число х,
удовлетворяющее условиям:
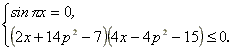
- Найдите все действительные значения а,
для каждого из которых уравнение
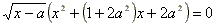 имеет только два различных
корня, найдите их.
имеет только два различных
корня, найдите их.
cos2x – (a + 7) cos x + (4 – a)(2a + 3) = 0 имеет решения. (Решение: см. приложение №2)
(Решение: см. приложение №3)
(Решение: см. приложение №4)
2a2 + 10a + 13) sin2x + 2(a + 2) sin x + 1 = 0 имеет решения.
(Решение: см. приложение №5)
(Решение: см. приложение №6, рисунок 1)
(Решение: см. приложение №7, рисунок 2)
(Решение: см. приложение №8)
(Решение: см. приложение №9)
(Решение: см. приложение №10)
(Решение: см. приложение №11)
(Решение: см. приложение №12, рисунок 3)
(Решение: см. приложение №13)
(Решение: см. приложение №14, рисунок 4)
(Решение: см. приложение №15, рисунки 5, рисунок 6)
(Решение: см. приложение №16, рисунок 7)