Описанное ниже исследование явилось результатом совместного творчества учителя и группы ребят, увлекающихся математикой и программированием. Совместная работа над этой проблемой показала креативные возможности соединения математики и информатики.
Следует отметить, что математическую сторону исследования можно поручать одним учащимся, построение модели математического явления – другим, а можно организовать работу так, чтобы исследование осуществлялось от начала и до конца одной и той же группой учеников. Всё зависит от их интересов, возможностей, и т. д.
Мы убеждёны в плодотворности и перспективности подобных занятий, ибо именно на стыке наук рождаются открытия!
В этой работе мы будем рассматривать решение нелинейного диофантова уравнения вида axy+bx+cy=d, где a, b, c, d – целые числа, и решение отыскивается также среди целых чисел.
Если a=0, то уравнение принимает вид bx+cy=d; решение этого классического уравнения подробно описано в литературе, программа его решения на компьютере опубликована http://morozko1967.narod.ru/soft.htm.
Пусть a
0. Тогда
уравнение
axy+bx+cy=d (1)
можно записать в виде
y(ax+c)+bx=d (2).
Зададим себе вопрос: может ли ax+c быть равным нулю? Да, если c делится на a и x= –c/a. Тогда решение существует, если bx=d, иными словами, bc+ad=0. Итак, мы получили такой вывод: если bc+ad=0 и c делится на а, то существует решение:
x= –c/a, y – любое целое число.
Точно также, если b делится на а, то существует решение
x – любое число, y= –b/a. Если bc+ad=0, но ни с, ни b не делятся на а, то решений нет.
Пусть теперь bc+ad0.
Тогда нет целого х, обращающего в 0 выражение (ax+c).
В этом случае уравнение можно записать в виде
Докажем, что уравнение (3) имеет конечное число целочисленных решений. Рассмотрим функцию
Естественно, эта функция является биекцией. Графиком функции является гипербола.
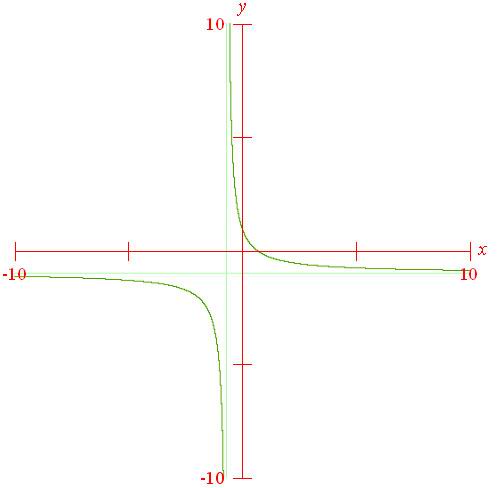
Заметим, что
Значит, при достаточно больших значениях переменной х значение переменной y близко к
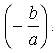
Между какими целыми числами заключено это число?
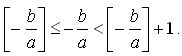
Начиная с некоторого значения переменной х переменная y, стремясь к
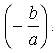
и остаётся дробной. Точно также, если отрицательное х велико по модулю, то переменная y, стремясь к
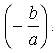
и остаётся дробной. Следовательно, уравнение (3) имеет конечное число целочисленных решений, и их можно поручить отыскать компьютеру простым перебором.
Но для этого необходимо найти отрезок на оси абсцисс, вне которого гарантированно нет целочисленных решений уравнения (3).
Если b не делится на а, то, очевидно, что границы целочисленных х равны
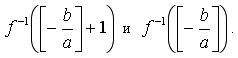
Если b делится на а, то границы целочисленных х равны
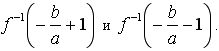
Рассмотрим эти два случая отдельно.
Случай 1. Пусть сначала b не делится на а. Найдём
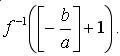
Обозначим
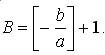
Числа
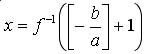
и y=B удовлетворяют уравнению (1). Поэтому
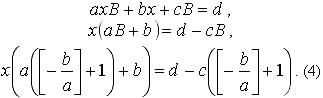
Далее нам потребуется…
Лемма. Пусть a, b – целые, отличные от нуля. Тогда
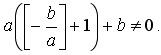
Если b не делится на а, то
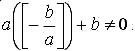
Доказательство.
Сначала докажем, что для любого нецелого х
[–x]+1=–[x]. (5)
Действительно, по определению целой и дробной частей
x=[x]+{x}, –x=[–x]+{–x};
{–x}=1–{x},
[–x]+1= – x–{–x}= –x–1+{x}=–x–(1-{x})= –x–{–x}=[–x].
Итак, [–x]= –[x]–1.
Допустим противное, пусть
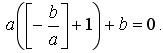
Возможны два случая: b делится на а, и b не делится на а. Если b не делится на а, то из (5) получаем
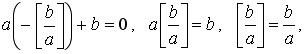
то есть b делится на а, что невозможно.
Если же b делится на а, то
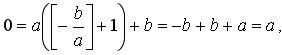
По условию а отлично от нуля. Полученное противоречие доказывает, что
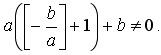
Докажем теперь второе неравенство леммы. Пусть b не делится на а. Допустим противное,
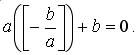
Тогда
Но это означает, что b делится на a. Полученное противоречие доказывает, что если b не делится на а, то
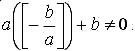
Лемма доказана.
Доказанная лемма позволяет из соотношения (4) найти
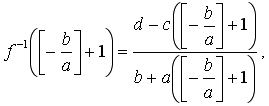
и в случае, если b не делится на а
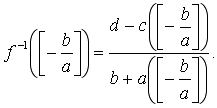
Обозначим
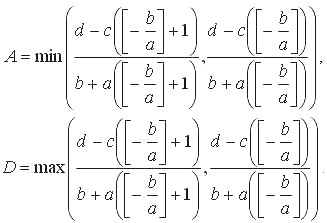
Тогда все целочисленные решения уравнения (3) удовлетворяют оценке
A
xD,
и уравнение (3) можно решить простым перебором, беря по очереди целые значения х от А до D, вычисляя соответствующие
и проверяя, является ли найденное значение у целым. Если d–bx делится на ax+c, то существует решение
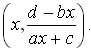
Случай 2. Пусть b делится на а. Тогда границы целочисленных х равны
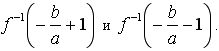
Найдём сначала
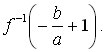
Обозначим
Тогда F удовлетворяет соотношению
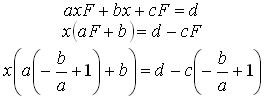
Учитывая, что в этом случае b делится на а, получаем:
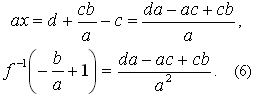
Теперь найдём
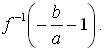
Обозначим
Тогда G удовлетворяет соотношению
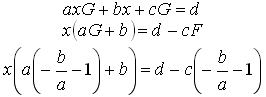
Учитывая, что в этом случае b делится на а, получаем:
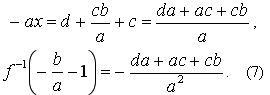
Обозначим
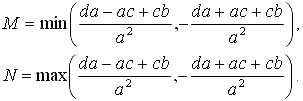
Тогда все целочисленные решения уравнения (3) удовлетворяют оценке
MxN,
и уравнение (3) можно решить простым перебором, беря по очереди целые значения х от А до D, вычисляя соответствующие
и проверяя, является ли найденное значение у целым. Если d–bx делится на ax+c, то существует решение
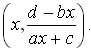
Итак, оба случая рассмотрены, осталось написать программу для персонального компьютера.
Исходный код программы на языке Pascal можно посмотреть в <Приложениии 1>, а также мы разместили его здесь: http://guopolysaevo.narod.ru/arc/sdiof17.zip.