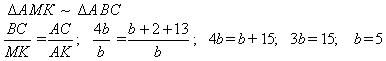1. Развитие интеллектуального творчества учащихся, привлечение их к исследовательской деятельности в науке.
2. Выявление способных и одарённых учащихся.
3. Подготовка ученика 11 класса к выполнению работы, носящей характер научного исследования по теме: "Построения одним циркулем с ограниченным раствором".
4. Подготовка ученика 7 класса к выполнению работы "Применение геометрии к решению текстовых задач".
5. Представление работ на Краевую научно-практическую конференцию школьников "Эврика".
Первый этап руководства
Прежде чем осуществить руководство исследовательской работой школьников, таких школьников надо выявить, что можно сделать на уроках или на занятиях математического кружка. В процессе занятий на уроках и на кружках создаётся математическая база для дальнейшей творческой работы школьника. Необходимым условием творческой деятельности школьника является наличие математической базы и желание школьника заниматься творческой деятельностью. Руководство исследовательской работой школьника осуществляется через практическую деятельность, т.е. через решение задач. В процессе решения задач предусматривается математическое развитие ученика. Руководитель должен научить школьника варьированию условий задачи как средству активизации мыслительной деятельности. Варьирование - это решение задач различными способами, составление и решение обратных задач, превращение задачи в более простую и наоборот, получение различных выводов из уже решённой задачи, рассмотрение её частных случаев, обобщение задачи, составление задачи, аналогичной к уже решенной. На занятиях математического кружка руководитель должен показать, как составлять новые задачи, давать поисковые задания, предполагающие при их выполнении проявление наблюдательности, обращение к анализу, синтезу, сравнению, индукции.
Необходимо подбирать блоки родственных заданий, объединённых одной математической идеей или проблемой.
Второй этап руководства
1. Сформулировать проблему.
2. Дать школьнику тему доклада для представления на Краевую научно-практическую конференцию школьников "Эврика".
3. Дать школьнику для решения и исследования задачи, не встреченные мной в литературе (составлены руководителем).
4. Предложить школьнику найти свои интересные задачи по теме, рассмотреть различные случаи, осуществить поиск других способов решения предложенных руководителем задач, изменить некоторые условия задач или рассмотреть задания с другими ограничениями.
5. Проводить индивидуальные консультации по возникающим у школьника вопросам.
6. Проверка и корректировка руководителем реферата по предложенной теме.
7. Помочь школьнику в подборе соответствующей литературы.
В данной программе научно-методической деятельности по руководству исследовательской работой школьников показаны перечисленные этапы руководства на примере "Подготовка по теме "Построение одним циркулем с ограниченным раствором".
1. Пункты А, Б соответствуют первому этапу руководства. Все задачи из пунктов А, Б следует решать на занятиях математического кружка, здесь же проходится соответствующая теория.
2. Пункты В и Г носят исследовательский характер, к задачам пункта А вводится дополнительно условие – а именно, раствор циркуля не может быть меньше некоторой величины r или не может превышать некоторую величину r. Задачи пунктов В и Г задаются школьникам на дом, а их решения проверяются на занятиях математического кружка, тем самым выявляются школьники, проявляющие интерес к данной теме (задаче) и успешно продвигающиеся в ней.
3. Пункты В и Г соответствуют второму этапу руководства. Школьники (1-3 человека), имеющие существенные достижения при решении задач пунктов В и Г продолжают научно-исследовательскую работу по данной теме.
- Руководитель формулирует задачи 1-6 (станицы 2-3 данной работы) и предлагает их для решения школьникам.
- Руководитель предлагает составить свои новые задачи, рассмотреть другие интересные случаи, с другими ограничениями.
- Руководитель проводит индивидуальные консультации для этой группы школьников.
- Представить все (1-2-3) доклады на школьную научно-практическую конференцию старшеклассников "Шаг в будущее". В каждом докладе подчеркнуть свои новые найденные моменты.
- Из 2-х – 3-х докладов выбрать лучший и представить на Краевую научно-практическую конференцию "Эврика".
I. Подготовка по теме:
"Построение одним циркулем с ограниченным раствором"
Традиционное ограничение орудий геометрических построений только циркулем и линейкой восходит к глубокой древности. При этом циркуль и линейка рассматривались как равноправные инструменты. В 1672 году датский геометр Г. Мор (а в 1797 году и итальянец Маскерони) доказал, что любое построение, которое выполняется циркулем и линейкой, можно проделать с помощью одного циркуля. Уже давно было замечено, что циркуль является более точным, более совершенным инструментом, чем линейка. Но с помощью циркуля нельзя проводить прямые, поэтому прямая считается построенной, если построены две её точки. И всё же самый большой интерес у геометров вызывали задачи, в которых рамки дозволенного не расширялись, а сужались. В литературе рассмотрено много задач на построение одним циркулем с ограничениями раствора.
Цель работы ученика: решить самостоятельно новые задачи с ограничениями, например такие:
Задача 1
Даны два отрезка АВ и DE. На АВ
находится точка С. Найти на DE такую точку F,
чтобы
при условии АС < r, АВ < r, ВС
< r, DE – любой отрезок, r – некоторая
величина.
Задача 2
Постройте отрезок в n раз меньше данного. Дано: АС
< r, АВ < r. DЕ – любой отрезок,
меньше r. Построить DF = , где n – любое
натуральное число.
Задача 3
Построить точки пересечения данной окружности и прямой, заданной двумя точками, если известно, что центр окружности не лежит на этой прямой, при условии, что диаметр окружности меньше раствора циркуля.
Задача 4
Построить прямую, перпендикулярную данному
отрезку и проходящую через один из его концов,
если а) r < R, < R < АВ б) АВ < r. R
– некоторая величина, АВ – некоторый отрезок.
Задача 5
Постройте центр начерченной окружности, если диаметр этой окружности меньше r.
Задача 6
Разделить дугу окружности пополам, если r R,
< R <AB
, радиус данной окружности больше R.
- Предложить ученику придумать свои задачи и привести их решения.
- При нахождении решений вышеизложенных задач необходимо опираться на известную теорему Мора-Маскерони, список всех аксиомных задач, употреблённых при построении циркулем и линейкой, а также на решения известных задач на построение с помощью одного циркуля без ограничений. Эти задачи ученик должен прорешать, а соответствующую теорию изучить.
Программа изучения этой темы:
А. Решить задачи с помощью одного циркуля без ограничений.
1. Построить точку, симметрично данной точке относительно данной прямой.
2. Как с помощью одного циркуля определить, лежат ли три данные точки на одной прямой?
3. Построить отрезок в два раза больше данного.
4. Построить отрезок в n раз больше данного отрезка.
5. Даны три отрезка: а, b, с. Построить такой отрезок x, что
.
6. Построить центр начерченной окружности.
7. Разделить данную дугу окружности пополам.
8. На прямой, заданной двумя точками постройте: а) одну точку; б) любое наперёд заданное количество точек.
9. Постройте середину данного отрезка.
10. Постройте точки пересечения данной окружности и прямой, заданной двумя точками, если известно, что центр окружности не лежит на этой прямой.
11. Постройте точки пересечения данной окружности и прямой, заданной двумя точками, если известно, что центр окружности лежит на этой прямой. Случай 1: прямая задана двумя точками A и B, центр O лежит на прямой АВ. Случай 2: пусть прямая проходит через центр, т.е. задана двумя точкам O и А. Случай 2 решить двумя способами. Один из них более громоздкий, но интересный, для этого решите следующие задачи:
а) построить отрезок
с помощью одного циркуля, p > q; б) построить отрезок
, если отрезок длины a задан; в) построить отрезок
; г) по данным отрезкам p и q построить отрезки
и m2 = 2p2 – (p2 – q2).
12. Построить точку пересечения прямых АВ и CD, каждая из которых задана двумя точками (А и B лежат по разные стороны CD).
Для решения этой задачи решить три вспомогательных задачи: a) из точки вне прямой опустить перпендикуляр на прямую; б) даны два отрезка АВ и DE. На АВ находится точка С. Найти на DE такую точку F, чтобы
; в) построить параллелограмм ABCD на трёх точках A, B, C, не лежащих на одной прямой.
13. Докажите теорему Мора-Маскерони: все задачи на построение, разрешимые циркулем и линейкой, могут быть точно решены одним только циркулем.
14. Одним циркулем постройте прямую, перпендикулярную данному отрезку и проходящую через один из его концов. Постарайтесь обойтись как можно меньшим количеством построений (одно построение – это один замер циркулем расстояния или проведение одной окружности (дуги)).
15. Постройте отрезок в n раз меньше данного. За какое наименьшее количество построений это можно сделать?
16. Одним циркулем построить правильный треугольник, четырёхугольник, шестиугольник, пятиугольник.
17. Найти свои интересные задачи.
Б. Изучить тему "Инверсия".
1. Определение инверсии.
2. Свойства инверсии.
3. Построение обратных точек с помощью одного только циркуля.
4. Построить одним только циркулем окружность l', являющуюся образом при инверсии относительно окружности с центром O прямой l, не проходящей через точку О. Прямая задана двумя точками X и У.
5. Рассмотреть другие интересные задачи.
6. После изучения темы «Инверсия» решить с помощью инверсии задачи 6, 10, 12 из пункта A.
В. Решить задачи 1, 2, 3, 4, 5, 8, 9, 11, 15 из пункта A, если дополнительно раствор циркуля не может быть меньше некоторой величины r. Этим же способом решить следующие задачи:
1. Из точки вне прямой АВ опустить перпендикуляр на прямую АВ. АВ < r.
2. Разделить данную дугу окружности пополам (диаметр окружности меньше r).
3. Постройте точки пересечения данной окружности и прямой, заданной двумя точками, если известно, что центр окружности лежит на этой прямой (диаметр окружности меньше r).
4. Даны два отрезка АВ и DE. На АВ находится точка С. Найти на DE такую точку F, чтобы
, где АС < r, АВ < r, CB < r. DE – любой отрезок.
5. Построить точку пересечения двух прямых АВ и CD, каждая из которых задана двумя точками, причём АВ < r и точки A и B находятся по одну сторону от точек C и D.
6. Построить центр начерченной окружности (диаметр окружности меньше r).
7. Постройте прямую, перпендикулярную данному отрезку AB (AB < r) и проходящую через один из его концов.
Г. Решить задачи с помощью одного только циркуля, раствор которого не может превышать некоторой величины R. Эти задачи носят исследовательский характер. К таким задачам относятся следующие задачи:
1. Постройте точку, симметричную данной точке относительно данной прямой (раствор циркуля меньше или равен R,
< R < АВ). АВ - некоторый отрезок данной прямой.
2. Построить отрезок в два раза больше данного отрезка (
< R < АВ).
3. Постройте отрезок в n раз больше данного отрезка (все условия предыдущей задачи выполняются).
4. На прямой, заданной двумя точками, постройте: а) одну точку; б) любое наперёд заданное количество точек.
5. Построить середину данного отрезка АВ;
< R < АВ.
6. Постройте точки пересечения данной окружности, заданной двумя точками, если известно, что центр окружности не лежит на этой прямой (раствор циркуля не превышает некоторой величины R;
< R < АВ, радиус окружности больше R).
7. Постройте прямую, перпендикулярную данному отрезку АВ и проходящую через один из его концов.
< R < AB. Вспомогательные задачи: а) из точки вне прямой АВ опустить перпендикуляр на прямую АВ; б) даны два отрезка АВ и ЕD. На АВ находится точка С. Найти на ED такую точку F, чтобы
(раствор циркуля меньше R,
< R < АВ,
< R < CD).
8. Предложить школьнику рассмотреть другие интересные случаи, с другими ограничениями, а также задачи 1-6, сформулированные на страницах 2-3 данной работы.
II. Подготовка по теме:
"Применение геометрии к решению текстовых задач".
Цель работы ученика:
1) изучить применение некоторых известных геометрических (графических и графико-вычислительных) приёмов к решению разнообразных арифметических и алгебраических задач по книге А.Н. Островский, Б.А. Кордемский " Геометрия помогает арифметике";
2) найти свои геометрические приёмы для решения текстовых задач.
Программа изучения темы:
1. Применение одномерных диаграмм к решению текстовых задач.
2. Применение двумерных диаграмм к решению текстовых задач.
3. Применение графика линейной функции к решению текстовых задач.
4. Применение графика равномерного движения к решению текстовых задач.
5. Прорешать известные задачи по вышеперечисленным темам.
6. Придумать свои задачи по вышеназванным темам и решить их.
7. Найти свои геометрические приемы для решения текстовых задач.
- С помощью одномерных диаграмм предложить ученику решить задачи типа:
1) В семейном детском доме живут несколько мальчиков и девочек. Мальчика спросили: "'Сколько у него братьев и сестер?" Он ответил: " У меня сестер в 3 раза меньше, чем братьев". Сестре задали тот же самый вопрос. На что она ответила: " У меня сестер в 4 разе меньше, чем братьев". Сколько всего детей в этом детском доме?
2) Несколько мальчиков ловили рыбу. Весь улов они разделили так:
Первый получил 2 штуки и 0.1 остатка.
Второй получил 4 штуки и 0.1 второго остатка.
Третий получил 6 штук и 0.1 третьего остатка.
Четвертый получил 8 штук и 0.1 нового остатка и т.д.
Оказалось, все получили поровну. Сколько штук рыбы было распределено? Сколько было мальчиков?
3) У Ивана было 3 лепёшки, а у Петра 4. Прохожий присоединился к их трапезе, заплатив 7 копеек. Все ели поровну. Как следует распределить деньги между Петром и Иваном?
- С помощью двумерных диаграмм предложить ученику задачи типа:
Поезд проходит расстояние от города А до города В за 10 часов 40 минут. Если бы скорость была на 10 км/ч меньше, то он пришёл бы в B на 2 часа 8 минут позже. Определить расстояние между городами и скорость поезда.
- По теме "Применение графика линейной функции" решить задачи, связанные с возрастом. Например, такие:
1) Когда отцу было 27 лет, сыну было 3 года. Сейчас сыну в 3 раза меньше лет, чем отцу. Сколько лет каждому из них?
2) Теперь мне вдвое больше лет, чем было Вам тогда, когда мне было столько лет, сколько Вам теперь. Когда Вам будет столько лет, сколько мне теперь, то нам вместе будет 90 лет. Сколько теперь лет каждому?
3) Брат говорит сестре: "Когда тёте Кате было столько лет, сколько теперь нам с тобой вместе, то тебе было столько лет, сколько мне сейчас. А вот когда тёте Кате было столько лет, сколько тебе сейчас, то тогда тебе было... Сколько лет было сестре?
- По теме "График равномерного движения" прорешать задачи типа:
Два туриста выезжают одновременно навстречу друг другу из двух пунктов A и B. При встрече оказалось, что первый проехал на 30 км более второго, и что через 4 дня он будет в пункте B. Второй попадает в пункт A через 9 дней после встречи. Найти расстояние АВ.
- Предложить ученику найти свои геометрические приемы, которых нет в книге, например такой:
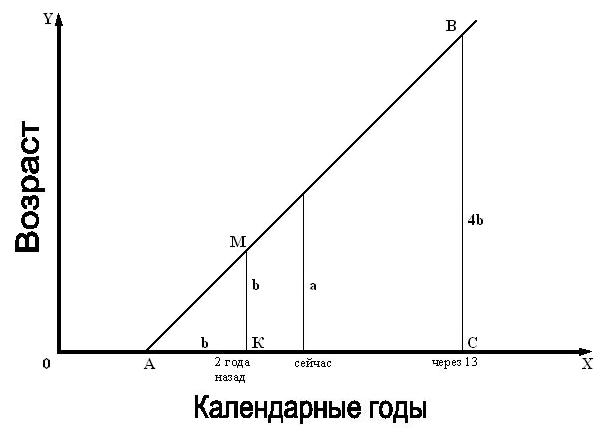
Решить задачу: Мальчик на вопрос: " Сколько ему лет?" отвечал, что через 13 лет ему будет в 4 раза больше, чем ему было 2 года назад. Сколько лет мальчику?
Решение:
Построим график возраста мальчика. Пусть последовательность дат календарных лет мальчика изображается точками оси ОХ. На оси ОУ будем изображать возраст мальчика. График возраста - прямая АВ - одинаково наклонённая к оси ОУ и ОХ.
Пусть a лет мальчику сейчас, b лет было мальчику 2 года назад МК = АК = b, 4b лет будет мальчику через 13 лет ВС = 4b.
a = b + 2; a = 7
Ответ: 7.
Рисунок 1.
Литература
По теме: «Построение одним циркулем с ограниченным раствором»:
1. Понарин Я. П. Геометрия для 7х-11х классов: Планиметрия. – Ростов-на-Дону: Феникс, 1998. – С. 431-444.
2. Зетель С.И. Геометрия линейки и геометрия циркуля. – М.: Учпедгиз, 1957.
3. Костовский А. Н. Геометрические построения одним циркулем. – М.: Наука, 1984.
4. Куранти Р., Роббинс Г. Что такое математика?. – М.: Просвещение, 1967. –
С. 170-176.
5. Прасолов В.В. Задачи по планиметрии: В 2 ч. – Ч. 2. – М.: Наука, 1991. – С. 184-191.
6. Брудно. А.Л.Вокруг циркуля.// Квант – 1974 – №10 – С. 1-9.
7. Квант – 1987 – №б.
По теме: «Применение геометрии к решению текстовых задач»:
8. Островский А. Н., Кордемский Б. А. Геометрия помогает арифметике. – М.: Физматгиз, 1960.
9. Спивак А. В. Математический праздник. – М.: Бюро Квантум, 2000. (Прил. к журналу "Квант" № 4/2000)
10. Зубелевич Г. И. Сборник задач московских математических олимпиад издательство М.: Просвещение,1967.
11. Математика 6-8. – М.: Бюро Квантум, 1998 (Прил. к журналу "Квант" №3/1998)