Предисловие.
Дети очень любят выполнять задания своими нестандартными методами, с большим интересом относятся ко всему новому, желают превзойти своих учителей, быть замеченными среди товарищей и стремятся к повышению своих результатов. При решении задач по математике, информатике, и другим предметам, выполнении производственных заданий они ищут собственные рациональные методы их решения с наименьшими затратами труда и средств. Во время поиска выхода из тупиковых ситуаций оригинальным методом глаза детей загораются яркими огоньками, на их лицах появляется радостная, озабоченная улыбка. В таких ситуациях учителю необходимо оказывать помощь в выборе способов решений данных заданий и совместно искать пути и методы для рационального достижения результата.
Так, при изучении формул приведения
тригонометрических функций, учащийся Кондратьев
Роман пытается доказать верность формулы
приведения ![]()
![]() с помощью формулы сложения
с помощью формулы сложения ![]() , заменяя в ней
величину
, заменяя в ней
величину ![]() на
значение
на
значение ![]() ,
получает следующий вид
,
получает следующий вид 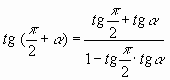 .
.
Из определения тангенса известно, что 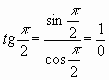 , то есть
действительных чисел для определения величины tg
, то есть
действительных чисел для определения величины tg![]() в настоящий период нет.
Тригонометрические функции определяют законы
поворота точки (1; 0) единичной окружности вокруг
начала координат, которая является материальной
и поворачивается беспрерывно, что даёт
возможность предполагать о существовании
зависимости функций
в настоящий период нет.
Тригонометрические функции определяют законы
поворота точки (1; 0) единичной окружности вокруг
начала координат, которая является материальной
и поворачивается беспрерывно, что даёт
возможность предполагать о существовании
зависимости функций 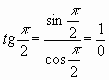 , а также наличия функции
, а также наличия функции ![]() , величина которой обладает
нестандартными свойствами и не входит в область
действительных чисел. Для определения свойств
величины
, величина которой обладает
нестандартными свойствами и не входит в область
действительных чисел. Для определения свойств
величины ![]() и
решения задачи учащегося Кондратьева Романа его
нестандартным способом проводится следующий
урок.
и
решения задачи учащегося Кондратьева Романа его
нестандартным способом проводится следующий
урок.
Цель урока: оказать помощь учащемуся Кондратьеву Роману, его товарищам в решении задачи их способом и развить самостоятельные навыки в творческой деятельности учащихся.
Тип урока: Урок собственных открытий.
Задачи:
- Привить любовь к творческому труду и решению задач собственными силами.
- Научить учащихся выявлять законы развития окружающего их мира с целью решения задач, повышения благосостояния общества и сохранения окружающей среды.
- Продолжить формирование нравственных качеств учащихся, их интеллекта и творческой личности.
Оборудование: компьютерный класс, программы Microsoft Office, проектор, учебники, индивидуальные задания.
Продолжительность занятий: 2 часа.
ХОД ЗАНЯТИЙ
I. Проверка готовности учащихся к занятиям.
Проверяется наличие учащихся в классе, их состояние, отношение к умственному труду, наличие и качество учебного оборудования, дидактических материалов.
II. Сообщение цели урока и метода её достижения.
Требуется решить задание учащегося
Кондратьева Романа, предложенным им способом,
определить свойства величины ![]() и найти им применение при решении
задач теоретического и прикладного характера.
Для поиска свойств величины
и найти им применение при решении
задач теоретического и прикладного характера.
Для поиска свойств величины ![]() предлагается сравнить формулы
определения площади треугольника по стороне и
двум прилежащим к ней углам при величине одного
из углов равной
предлагается сравнить формулы
определения площади треугольника по стороне и
двум прилежащим к ней углам при величине одного
из углов равной ![]() .
.
(1) ![]() (2)
(2) ![]() , где S – площадь
треугольника, c – длина стороны треугольника,
, где S – площадь
треугольника, c – длина стороны треугольника,
![]() и
и ![]() величины углов, прилежащих
к стороне c. Если один из прилежащих углов к
стороне с треугольника будет 90°, то формула (1)
упрощается и примет вид формулы (2).
величины углов, прилежащих
к стороне c. Если один из прилежащих углов к
стороне с треугольника будет 90°, то формула (1)
упрощается и примет вид формулы (2).
Формулы (1) и (2) учащиеся изучают в училище, а также
им предлагается ознакомиться с ними на сайте
интернета https://urok.1sept.ru,
фестивале педагогических идей “Открытый урок”
2003/2004 учебного года или в статье “Площадь
треугольника. Новые задачи” еженедельного
учебно-методического приложения к газете
“Первое сентября”, “Математика” №2, 1999 года.
Приравниваем правые части формул (1) и (2) , когда
величина ![]() =
= ![]() = 90° , так как в этом
случае они равны. Делаем тождественное
преобразование в получившемся равенстве
= 90° , так как в этом
случае они равны. Делаем тождественное
преобразование в получившемся равенстве ![]() =
= ![]() путём умножения левой и правой
частей на множитель
путём умножения левой и правой
частей на множитель ![]() , который является в данном случае
положительным числом, получим
, который является в данном случае
положительным числом, получим ![]() .
. ![]() =
= ![]() .
.
![]() или
или ![]() . Из получившегося
результата видно, что числитель и знаменатель в
левой части дроби равны между собой, то есть
. Из получившегося
результата видно, что числитель и знаменатель в
левой части дроби равны между собой, то есть ![]() .
.
Результат обнаружил уникальное свойство
величины ![]() ,
которого нет у действительных чисел. Величина
,
которого нет у действительных чисел. Величина ![]() не изменяется, если
к ней прибавить действительное число.
не изменяется, если
к ней прибавить действительное число.
Это и есть открытие данного урока.
Для краткой записи величину ![]() обозначим знаком Тn, назовём тьмой,
то есть Тn =
обозначим знаком Тn, назовём тьмой,
то есть Тn = ![]() =
= ![]() , где 0n —
равняется величине материальной точки (1;0),
поворачивающейся вокруг начала координат по
дуге единичной окружности согласно определения
тригонометрических функций, при которой n –
мерные пространства переходят в (n-1) –
пространства. Число 0n назовём словом мал и
определим как величину являющуюяся обратной
числу тьма
, где 0n —
равняется величине материальной точки (1;0),
поворачивающейся вокруг начала координат по
дуге единичной окружности согласно определения
тригонометрических функций, при которой n –
мерные пространства переходят в (n-1) –
пространства. Число 0n назовём словом мал и
определим как величину являющуюяся обратной
числу тьма ![]() .
.
Свойства новых чисел тьма и мал.
, где а любое действительное
число, то есть величина числа тьма не изменяется,
если к нему прибавить действительное число, что
было доказано выше. Из этого свойства видно, что
здесь нарушается аксиома Архимеда, которая
утверждает, что для любых двух чисел а и b, где
0 < a < b, одно из неравенств a+ a > b, a+ a+ a > b,
… обязательно выполнено.
![]() . Последние
равенства пункта 5 показывают, что величина
действительного числа не изменится, если к нему
прибавить число мал или действительное
число, умноженное на число мал. В этом
свойстве также нарушается аксиома Архимеда, о
которой говорилось выше.
. Последние
равенства пункта 5 показывают, что величина
действительного числа не изменится, если к нему
прибавить число мал или действительное
число, умноженное на число мал. В этом
свойстве также нарушается аксиома Архимеда, о
которой говорилось выше.
Аксиомы чисел тьма и мал для проведения других арифметических операций между собой и с действительными числами на этом уроке не спонадобятся и предлагается учащимся подумать над ними самостоятельно.
III. Доказательство формулы приведения ![]() методом учащегося
Кондратьева Романа с помощью нестандартных
свойств величины
методом учащегося
Кондратьева Романа с помощью нестандартных
свойств величины ![]() .
.
У доски работает Кондратьев Роман, а остальные
работают звеньями по четыре человека в звене за
своими партами.
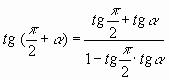 =
= ![]() .
.
Данное доказательство показывает
справедливость формулы приведения и
существование величины ![]() со своими необычными свойствами,
которые учащиеся нашли на уроке под руководством
учителя.
со своими необычными свойствами,
которые учащиеся нашли на уроке под руководством
учителя.
IV. Самостоятельная работа на уроке.
Группа учащихся разбивается на звенья (по 3, 4 человека в звене), старшими в звеньях назначаются наиболее активные учащиеся, которые получают для своего звена компьютеры и дидактический материал.
Задачи первого варианта.
Задача № 1.
Определить площадь лесного участка, имеющего вид близкий к форме треугольника, который ограничен двумя речками и дорогой (см. рис.1). Длина дороги 1354 метра, а углы, прилежащие к ней, соответственно равны 90° и 47°. Для решения задачи используйте электронную таблицу Excel и формулу (1) определения площади треугольника по стороне и двум прилежащим к ней углам.
Ход решения задачи № 1 первого варианта.
Сначала звено должно преобразовать формулу (1) с
помощью числа тьма в формулу вида (2), так как
один из прилежащих углов к дороге равен 90°, а
затем написать программу для решения этой задачи
с помощью электронной таблицы Excel, ввести её и
получить ответ. Преобразование формулы (1) в
формулу (2) ![]() .
.
Формула в Excel =1354^2*TAN(47/57, 3)/2 .
После выполнения программы получится ответ: ~
982876,3 м2
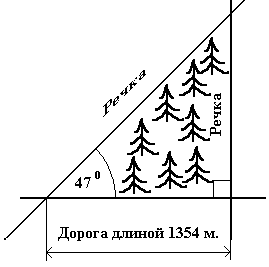
Рис. 1
Задача № 2.
Фермеру требуется сделать перекрытие на садовый домик, профиль которого будет иметь форму прямоугольного треугольника с гипотенузой 12 (м) и площадью 32 (кв. м.). Определить углы, прилежащие к гипотенузе, т. е. основанию перекрытия, чтобы точно сделать объект и оптимально израсходовать строительный материал. (См. рис. 2). Составьте программу для решения данной задачи в электронной таблице Excel.
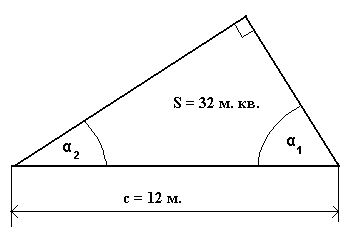
Рис. 2
Ход решения задачи № 2 первого варианта.
Эта задача рационально решается с помощью тригонометрического уравнения нашего училища (1), с которым можно глубже познакомится в указанной выше литературе.
Особенностью решения этой задачи является то, что угол напротив известной стороны дан величиной 90°. При применении тригонометрического уравнения нашего училища учащиеся должны будут преобразовать его к виду (2) нестандартным способом с помощью числа тьма.
(1) ![]() , где
, где
S – площадь профиля перекрытия = 32 (кв. м.), с –
длина основания (гипотенузы) = 12 (м.),
![]() = 90°, то есть tg
= 90°, то есть tg ![]() стандартным
способом не определён. Для решения данной задачи
уравнение (1) можно преобразовать к виду (2) без tg
стандартным
способом не определён. Для решения данной задачи
уравнение (1) можно преобразовать к виду (2) без tg ![]() способом,
данным в выше указанной литературе. Здесь
учащиеся должны использовать для перехода от
уравнения (1) к уравнению (2) числа тьма и мал,
так как изучили их свойства и этот способ более
рационален. Подставляя значение tg 90° = Tn в
уравнение (1), получат
способом,
данным в выше указанной литературе. Здесь
учащиеся должны использовать для перехода от
уравнения (1) к уравнению (2) числа тьма и мал,
так как изучили их свойства и этот способ более
рационален. Подставляя значение tg 90° = Tn в
уравнение (1), получат ![]() .
.
Откуда согласно свойств Tn уравнение (1) примет
следующий вид ![]() .
Последнее выражение после деления на Tn и
умножения на –1 получит окончательный вид,
необходимого для решения данной задачи,
уравнения (2).
.
Последнее выражение после деления на Tn и
умножения на –1 получит окончательный вид,
необходимого для решения данной задачи,
уравнения (2).
(2) ![]() .
.
В уравнение (2) подставляются данные из задачи №
2 ![]() .
.
Составляется программа решения последнего
тригонометрического уравнения, то есть для
определения корней tg ![]() 1 , tg
1 , tg ![]() 2 , а затем для нахождения
окончательных результатов — величин углов
2 , а затем для нахождения
окончательных результатов — величин углов ![]() 1 и
1 и ![]() 2 в
электронной таблице Excel.
2 в
электронной таблице Excel.
Программа в Excel.
| A | B | C | |
| 1 | 4 | -9 | 4 |
| 2 | =B1^2-4*A1*C1 | tg |
=ЕСЛИ(A2>=0;(-B1+КОРЕНЬ(A2))/(2*A1);”Нет корней”) |
| 3 | tg |
=ЕСЛИ(A2>=0;(-B1-КОРЕНЬ(A2))/(2*A1);”Нет корней”) | |
| 4 | =ATAN(C2)*57,3 | ||
| 5 | =ATAN(C3)*57,3 |
Результат выполнения данной программы в Excel.

После выполнения программы в Excel получили
ответы для задачи № 2. Углы между основанием
перекрытия и уклонами должны быть:
![]() 1 ~ 58,64° и
1 ~ 58,64° и ![]() 2 ~ 31,36°
2 ~ 31,36°
Задачи второго варианта
Задача № 3.
Определить площадь лесного участка, имеющего вид близкий к форме треугольника, который ограничен двумя речками и дорогой (см. рис.3). Длина дороги 1537 метров, а углы, прилежащие к ней, соответственно равны 90° и 33°. Для решения задачи используйте электронную таблицу Excel и формулу (1) определения площади треугольника по стороне и двум прилежащим к ней углам.
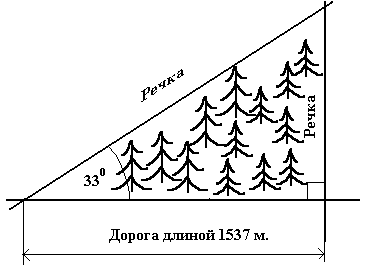
Рис. 3
Решение данной задачи аналогично решению задачи № 1 первого варианта.
![]() .
.
Формула в Excel =1537^2*TAN(33/57, 3)/2 .
После выполнения программы получится ответ: ~ 766998, 94 м2 .
Задача № 4.
Фермеру требуется сделать перекрытие на садовый домик, профиль которого будет иметь форму прямоугольного треугольника с гипотенузой 14 (м) и площадью 42 (кв. м.). Определить углы, прилежащие к гипотенузе, т. е. основанию перекрытия, чтобы точно сделать объект и оптимально израсходовать строительный материал. (См. рис. 4). Составьте программу для решения данной задачи в электронной таблице Excel.
Данная задача решается аналогично задаче № 2 первого варианта, то есть используется тригонометрическое уравнение училища (1), а затем оно преобразуется с помощью числа тьма к тригонометрическому уравнению вида (2).
![]() .
.
После подстановки данных задачи в это
уравнение оно примет следующий вид ![]() .
.
Получившиеся тригонометрическое уравнение решается с помощью электронной таблицы Excel аналогично задаче №2 первого варианта.
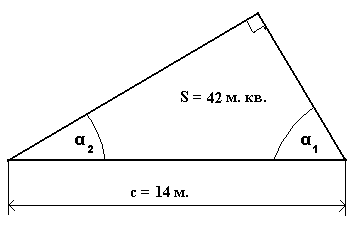
Рис. 4
Программа решения данной задачи в электронной таблице Excel.
| A | B | C | |
| 1 | 3 | -7 | 3 |
| 2 | =B1^2–4*A1*C1 | tg |
=ЕСЛИ(A2>=0;(-B1+КОРЕНЬ(A2))/(2*A1);”Нет корней” |
| 3 | tg |
=ЕСЛИ(A2>=0;(-B1-КОРЕНЬ(A2))/(2*A1);”Нет корней” | |
| 4 | =ATAN(C2)*57,3 | ||
| 5 | =ATAN(C3)*57,3 |
Результат выполнения данной программы в электронной таблице Excel.
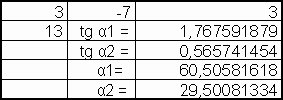
После выполнения программы получили ответы для
задачи №4: ![]()
VI. Подведение итогов урока.
Оценка 5 выставляется за точное преобразование
формул, уравнений для данных задач, составление
программ и получение правильных ответов.
Оценку 4 получают учащиеся, которые правильно
составили программы, но допустили ошибки при
вводе данных с клавиатуры, что привело к неточным
ответам.
Оценка 3 выставляется за решение задач с
небольшими ошибками, допущенными при
преобразовании формул, уравнений и составлении
программ.
VII. Домашнее задание.
- Найти на основании свойств чисел тьма и мал данного урока максимальную сумму чисел мал на интервале (0; 1).
- Определить углы между диагональю крышки своего рабочего стола и её сторонами, которые вместе с диагональю образуют прямоугольный треугольник. Рабочая поверхность стола должна быть прямоугольная. Решение задачи выполните с помощью тригонометрического уравнения училища (1), новых чисел тьма и мал, электронной таблицы Excel. После получения ответа сравните его со своими измерениями этих углов транспортиром и убедитесь в правильности своего решения.