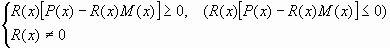Общее время основного государственного экзамена по математике 235 минут.
Экзаменационная работа состоит из 20 заданий базового уровня и 6 заданий повышенного уровня.
Неравенства являются заданиями, как первой, так и второй части.
Пользуясь приведенными алгоритмами, основанными на методе интервалов, по плану экзаменационной работы, на решение неравенства базового уровня отводим 3-5 минут, а задания повышенного уровня требуют 10-15 минут.
В основе метода интервалов лежат следующие свойства.
Первое свойство:
Двучлен (x-x0) имеет положительное значение для всех x, находящихся на числовой оси правее точки x0, и принимает отрицательные значения для всех x, находящихся слева от этой точки.
Второе свойство:
Многочлен Р(х)=![]()
при переходе через точку xi меняет знак, если ki - нечетное число, т.е. корень xi нечётной кратности, и не меняет знака, если kn - четное число, т.е. корень xi чётной кратности.
Пусть требуется решить неравенство
![]()
или ![]() , (1)
, (1)
где k1,k2, ..., kn-1,kn — фиксированные натуральные числа,
х1, х2, … хn-1,xn — фиксированные действительные числа, среди которых нет равных, и такие, что х1<х2< … <хn-1<xn .
Тогда неравенства вида (1) можно решить так называемым методом интервалов.
Рассмотрим многочлен
Р(х)=![]() (2)
(2)
Очевидно, что для любого числа yо, такого, что yо> хn, соответствующее значение любого сомножителя в произведении (2) положительно, поэтому числовое значение Р(yо) многочлена Р(х) также положительно.
Для любого числа y1, взятого из промежутка (xn-1,xn) , соответствующее числовое значение любого сомножителя, кроме последнего, положительно; соответствующее числовое значение последнего сомножителя положительно, если kn - четное число, и отрицательно, если kn - нечетное число. Поэтому число Р(y1) - положительно, если kn -четное число, и число Р(y1) - отрицательно, если kn - нечетное число. Обычно в этих случаях говорят, что многочлен Р(х) при переходе через точку xn меняет знак, если kn - нечетное число, и не меняет знака, если kn - четное число.
Аналогично показывается, что если известен знак многочлена Р(х) на промежутке (xi,xi+1), то на промежутке (хi-1,xi), знак определяется по правилу: многочлен Р(х) при переходе через точку xi меняет знак, если ki -нечетное число, и не меняет знака, если ki -четное число. Основываясь на этих рассуждении, пропишем алгоритм, дающих решение алгебраических неравенств вида (1).
Алгоритм
“Решение неравенств вида
![]() или
или
![]() ”
”
- на числовую ось нанести числа х1, х2, … хn-1,xn ;
- в промежутке справа от наибольшего из этих чисел, т. е. справа от хn, поставить знак “+”, в следующем за ним справа налево промежутке поставить знак “+”, если kn - четное число, и знак “-”, если kn- нечетное число;
- в следующем за ним справа налево промежутке ставят знак, пользуясь правилом: многочлен Р(х) при переходе через точку хn-1 , меняет знак, если kn-1 - нечетное число, и не меняет знака, если kn-l — четное число;
- затем рассматривается следующий за ним справа налево промежуток, в нем ставят знак, пользуясь тем же правилом;
- таким образом рассматриваются все промежутки.
- решением неравенства
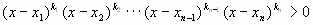 будет объединение всех
промежутков, в которых поставлен знак “+”;
будет объединение всех
промежутков, в которых поставлен знак “+”;
решением неравенства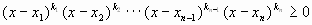 будет объединение всех
промежутков, в которых поставлен знак “+” с
включёнными в них числами х1, х2,
… хn-1,xn ;
будет объединение всех
промежутков, в которых поставлен знак “+” с
включёнными в них числами х1, х2,
… хn-1,xn ;
решением неравенства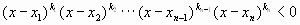 будет объединение всех
промежутков, в которых поставлен знак “-”;
будет объединение всех
промежутков, в которых поставлен знак “-”;
решением неравенства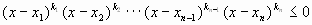 будет объединение всех
промежутков, в которых поставлен знак “-”с
включёнными в них числами х1, х2,
… хn-1,xn.
будет объединение всех
промежутков, в которых поставлен знак “-”с
включёнными в них числами х1, х2,
… хn-1,xn.
Алгоритм
“Решение неравенства вида R(х) > 0 (R(х)
![]() 0) или R(х)<0(R(х)
0) или R(х)<0(R(х) ![]() 0), где R(х) - многочлен
стандартного вида”
0), где R(х) - многочлен
стандартного вида”
- Многочлен R(х) = а0хn + а1хn-1+...+ап-1х
+ ап (а0
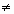 0) разложить
на множители и цепочкой равносильных переходов
данное неравенство представить в виде
0) разложить
на множители и цепочкой равносильных переходов
данное неравенство представить в виде 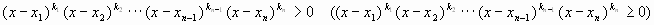 или
или 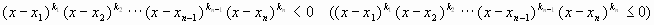
- на числовую ось нанести числа х1, х2, … хn-1,xn ;
- в промежутке справа от наибольшего из этих чисел, т. е. справа от хn, поставить знак “+”, в следующем за ним справа налево промежутке поставить знак “+”, если kn - четное число, и знак “-”, если kn - нечетное число;
- в следующем за ним справа налево промежутке ставят знак, пользуясь правилом: многочлен Р(х) при переходе через точку хn-1 , меняет знак, если kn-1 - нечетное число, и не меняет знака, если kn-l — четное число;
- затем рассматривается следующий за ним справа налево промежуток, в нем ставят знак, пользуясь тем же правилом;
- таким образом рассматриваются все промежутки.
- решением неравенства
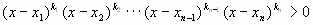 будет объединение всех
промежутков, в которых поставлен знак “+”;
будет объединение всех
промежутков, в которых поставлен знак “+”;
решением неравенства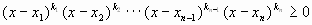 будет объединение всех
промежутков, в которых поставлен знак “+” с
включёнными в них числами х1, х2,
… хn-1,xn ;
будет объединение всех
промежутков, в которых поставлен знак “+” с
включёнными в них числами х1, х2,
… хn-1,xn ;
решением неравенства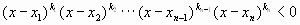 будет объединение всех
промежутков, в которых поставлен знак “-”;
будет объединение всех
промежутков, в которых поставлен знак “-”;
решением неравенства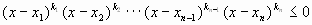 будет объединение всех
промежутков, в которых поставлен знак “-”с
включёнными в них числами х1, х2,
… хn-1,xn.
будет объединение всех
промежутков, в которых поставлен знак “-”с
включёнными в них числами х1, х2,
… хn-1,xn.
Вышеизложенные алгоритмы можно применять при решении алгебраических неравенств вида:
- V(х)>Q(х) ( V(х)
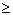 Q(х)) или
V(х)<Q(х) ( V(х)
Q(х)) или
V(х)<Q(х) ( V(х) 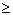 Q(х)).
Q(х)). 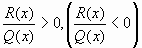 . Его
решение равносильно решению неравенства
. Его
решение равносильно решению неравенства 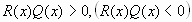
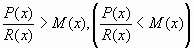 . Его
решение равносильно решению неравенства
. Его
решение равносильно решению неравенства 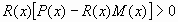 ,
,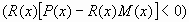
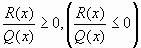 . Его
решение равносильно решению системы
. Его
решение равносильно решению системы 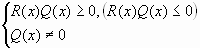
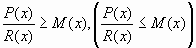 . Его
решение равносильно решению системы
. Его
решение равносильно решению системы