Решение задач с параметрами в курсе алгебры. 7–9-е классы

Разделы: Математика

Анализируя экзаменационные работы по математике, приходишь к выводу, что за курс математики в общеобразовательной школе учащимися должны быть отработаны умения решения задач с параметрами. Кроме непосредственной подготовки учащихся к экзаменам по данному разделу математики (решение задач с параметрами), главная его задача - поднять на более высокий уровень изучение математики в школе, следующий за развитием умений и навыков решения определенного набора стандартных задач. Ибо, решение задач с параметрами требует наличия определенного уровня математической культуры, навыков обобщения и разделения задачи на элементарные, аргументирования и обоснования своих действий, рассуждения на отвлеченном уровне, т.е. навыков проведения логических операций.

Знакомить учащихся с заданиями с параметрами следует, начиная с 7 класса, постепенно включая их в список задач к общему курсу.

  • В 7 классе представляется возможным вводить решение линейных уравнений с параметрами и простейших систем линейных уравнений с параметрами.
  • В курсе 8 класса следует разобрать способы решения некоторых типов уравнений второй степени с параметрами.
  • В 9 классе - рассмотреть расположение корней квадратного трехчлена в зависимости от параметра и решение связанных с этим вопросом системы заданий.

В курсе алгебры 7 класса в параграфе "Линейное уравнение с одной переменной" следует разобрать решение уравнения ах = в с неизвестным х как уравнение параметрами а и в. Здесь учащихся следует познакомить с понятием "параметры" (те переменные а, в, с, :, которые при решении уравнения считаются постоянными, или те коэффициенты, которые заданы не конкретными числами, а обозначены буквами).

На уроках обобщения, следующих за этим параграфом возможно разобрать решение линейного уравнения ах + в = с с неизвестным х и параметрами а, в, с.

В течение учебного года можно предлагать для решения задания следующего типа.

1. Решить уравнение с неизвестным х. (Решить уравнение с параметрами - значит указать при каких значениях параметров существуют решения и каковы они.)

1) рх =10; 7) ах - 3 = 2х + 5;
2) ах +7=8; 8) 3х + 4 = ах - 8;
3) вх - а = вх; 9) рх - 3 = 3х - р;
4) 3 - вх = 14; 10) к - 5х = -5 + кх;
5) ах + 3 = 3; 11) (а - 1)х + 2 = а + 1;
6) 2ах - 4 = 0; 12) ах + 2х + 3 = 1 - х;
13) а2(х - 5)=25(х - а).

Знакомить учащихся с решением систем линейных уравнений с параметрами следует начинать после изучения параграфа "Системы линейных уравнений с двумя переменными", котором разбирается графический способ решения систем линейных уравнений.

Предлагаются следующие задания.

Подобрать значения параметров а и в, чтобы:

а) система имела единственное решение;

б) система не имела решений

1) 2) 3) 4) 5)

Работая с последней системой, следует подробнее разобрать ответы на поставленные вопросы.

Решение. 1) если , то система примет вид

если т.е. система имеет единственное решение;

если = и т.е. и система не имеет решения;

2) если система примет вид и имеет единственное решение.

Ответ: если система имеет единственное решение;

если , , то система не имеет решения.

Решите систему уравнений с параметрами к и р, если :

1) 2)

Решение первой системы получается из знания взаимного расположения графиков линейных функций ( Ответ: (0;3)), решение второй системы предполагает умение решать системы линейных уравнений аналитическим методом.

Ответ: (1;3)

При всех значениях параметра а решить систему уравнений

Решение.

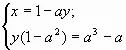
1) если , т.е. , то данная система равносильна

2) если а=1, то система имеет видх=1 - у

3) если а= - 1, то система равносильна уравнению х=1+у.

Ответ: при (1+а2; -а)

при а=1 (1-у; у)

при а=-1 (1+у; у)

Решите систему уравнений с двумя неизвестными х и у:

1) Ответ: если bа, то (-ab; b+a); если b=a, то (a2-ay; y).

2) Ответ: если b?, то x=1 y=b;если b=?,то x=2-3y, y- любое .

3) Ответ: при , то х=а-1, у=а;

при а=1, то х - любое число, у=1-х;

при а=-1, то х - любое число, у=1+х.

Задачи с параметрами для решения в 8 классе предполагают знания по теме "Квадратные уравнения", "Дробные рациональные уравнения", "Неравенства".

Задачи с параметрами, дополняющие список задач из учебника к теме "Квадратные уравнения".

Найдите к и второй корень уравнения:

х2 - 5х + к = 0, если х1=5;

х2 +кх - 15=0, если х1=3.

Найдите все числа р и с такие, что корни уравнения х2 + рх + с =0, равны р и с.

При каких а уравнение (1+а)х2+3ах - 1=0 имеет единственное решение?

Решите уравнение ах2=1.

Задания с параметрами, предлагаемые для выполнения после изучения темы "Неравенства".

1. Найдите все значения параметра а, для которых квадратное уравнение (а+1)х2 + 2(а+1)х+а-2=0 а) имеет два различных корня;

б) не имеет корней;

в) имеет два равных корня.

2. При всех а решите уравнение ах2 - 2х + 4= 0.

3. Решите уравнение ах2 + 2х + 1 = 0.

4. Найдите все значения параметра а, для которых уравнение 4х2 - 2х + а =0

а) имеет два различных корня;

б) не имеет корней.

5. Найдите все значения параметра а, для которых уравнение имеет единственный корень

а) ах2 - (2а+6)х + 3а + 3 = 0;

б) ах2 + (4а+2)х + 3а + 3/2 = 0.

После изучения главы I "Рациональные дроби" можно предлагать учащимся решать более сложные системы линейных уравнений с параметрами.

1. При всех значениях параметров а и в решить систему

1) 2) 3) 4) 5) 6)

Решение 1 системы.

если , , то ;

если 1+а=0, а = -1, то , чтобы система имела решение, необходимо,

чтобы в = -2, тогда , если , то решений нет.

Ответ: если , то (; )

если а = -1, в = -2, то (2+у; у)

если а = -1 , в-2, то решений нет.

В 9 классе представляется целесообразным после изучения главы I "Квадратичная функция" вернуться к решению уравнений второй степени с параметрами, предлагая учащимся для решения задания следующего типа.

1. Решите квадратные уравнения.

1) 2х2 - (а - 1)х + а + 1 = 0;

2) ах2 + (а + 1)х +а2 +а = 0;

3) ах2 + 2х(а + 1) + а +3 = 0;

4) (а - 2)х2 + ах + 1 = 0;

5) х2 - ах +2а + 4 = 0;

6) (а + 1)х2 - х + (1 - а) = 0.

2. Найдите все значения а, при которых уравнение имеет хотя бы один корень.

1) х2 - 2(а - 1)х + 2а + 1 = 0;

2) (а - 2)х2 - 2ах + 2а - 3 = 0.

3. Найдите все значения а, при которых сумма квадратов корней уравнения х2 - ах + а + 7 = 0 равна 10.

Решение. Так как Dimg1.gif (61 bytes)0, a2-4(a+7)?0, . Если а такое, что найдутся корни х1 и х2, то х1+х2=а и х1х2=а+7. х12+х22=(х1+х2)2 - 2х1х2=а2 - 2(а+7).

Решим уравнение а2 - 2а - 14=10, а=6, а = -4, т.к. 6 не принадлежит найденному множеству значений а, то а = -4. Ответ: а = -4.

4. Найдите все значения в, при которых уравнение имеет два различных корня.

1) (в - 1)х2 + 2х + 1 = 0;

2) вх2 - 2х - 2 = 0.

В конце учебного года в 9 классе на уроках "Повторение:" нужно познакомить учащихся с графическим методом решения уравнений 2-ой степени с параметрами, научить распознавать положение параболы на плоскости в зависимости от коэффициентов.

Для этого необходимо напомнить:

прямая х= - в/(2а) - ось параболы, х0= - в/(2а) - первая координата вершины параболы;

Знак коэффициента а показывает направление ветвей параболы;

Дискриминант D=b2 - 4ac определяет, пересекается ли парабола с осью Ох.

Указанные свойства парабол позволяют получить следующие факты, касающиеся расположения корней квадратного трехчлена на числовой оси.

1. Корни квадратного трехчлена х1 и х2 (f(х) = ах2+вх+с) будут строго меньше числа М, если выполняются следующие условия (очевидные, благодаря рисунку).

2. Если М I R, то х1< М < х2, в том и только в том случае, когда а*f(М) < 0.

a<0, f(M) >0

a>0, f(M) <0.

3. Оба корня х1 и х2 квадратного трехчлена f(х)=ах2+вх+с принадлежат интервалу(М;N), если и только если выполняются условия:

Задания, соответствующие другим случаям расположения корней квадратного трехчлена (оба корня больше некоторого числа М; если отрезок [М; N] целиком лежит на интервале (х1;х2) и другие) решаются, следуя аналогичным требованиям, проиллюстрированным на рисунке, который отвечает конкретному заданию.

1. При каких значениях а оба корня уравнения х2 - 6ах + 2 - 2а + 9а2= 0 больше трех?

.

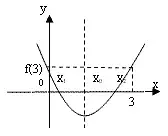
2. При каких значениях а оба корня уравнения х2 - ах +2 = 0 лежат на интервале (0;3)?

Ответ: .

3. При каких значениях а один корень уравнения ах2 +х +1 = 0 больше 2, а другой меньше 2?

Ответ: .

4. При каких значениях m оба корня уравнения (m+2)х2 - 2mх +3m = 0 положительны?

Ответ: -3 m < -2.

5. Найдите все значения а, при которых один из корней многочлена (а2+а+1)х2+(а -1)х +а2 больше 3, а другой меньше 3.

f(3)*a<0?, т.е.(10a2+12a+6) * (а2+а+1)<0.

Ответ: решений нет.

6. При каких значениях а один корень уравнения (а2+а+1)х2 +(2а - 3)х +(а - 5) = 0 больше 1, а другой меньше 1?

Ответ: .

7. При каких значениях а оба корня уравнения х2 +4ах + (1-2а+4а2) = 0 меньше -1?

Ответ: a>1.

8. Существуют ли такие а, что корни уравнения х2+2х+а=0 различны и лежат между числами -1 и 1?

Ответ: таких а не существует.

9. При каких значениях а оба корня уравнения (2 - а)х2 - 3ах +2а = 0 больше 1/2?

Ответ: .

10. При каких значениях а оба корня уравнения ах2 - (а+1)х +2 = 0 по модулю меньше 1?

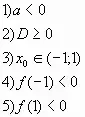
Ответ: .

11. Найдите все значения а, при которых уравнение 4х2 - 2х + а = 0 имеет два корня, каждый из которых принадлежит интервалу (-1;1).

Ответ: .

12. Найдите все значения а, при которых корни уравнения х2 - 2ах + а2 - 1 = 0 заключены между числами 2 и 4.

Литература.

  1. Д.К. Фадеев и др. "Задачи по алгебре для 6-8 классов", М., Просвещение, 1988
  2. В.В. Ткачук "Математика - абитуриенту", МЦНМО, ТЕИС, 1996
  3. С.А.Шестаков, Е.В.Юрченко "Уравнения с параметрами", СЛОГ, 1993
  4. Г.Я. Ястребинецкий "Задачи с параметрами", М., Просвещение, 1986
  5. В.В. Вавилов и др. "Задачи по математике. Алгебра", М., Наука, 1987
  6. Н.Я. Виленкин и др." Алгебра 8", М., Просвещение, 1995
  7. Л.И. Звавич др. "Задания для проведения письменного экзамена по математике в 9 классе", М., Просвещение, 1994
  8. В.В. Мочалов, В.В. Сильвестров "Уравнения и неравенства с параметрами", Чебоксары, Издательство Чувашского университета,2000
  9. А.Х. Шахмейстер "Уравнения и неравенства с параметрами",С.-Петербург, Москва, 2006