Цель: научить учащихся выполнять арифметические действиями в двоичной системе счисления.
Задачи:
образовательные:
- повторение и закрепление знаний учащихся о системах счисления;
- формировать у школьников умение выполнять правильно арифметические действия в двоичной системе счисления;
развивающие:
- развивать логическое мышление учащихся;
- развивать познавательный интерес учеников.
Содержание нового материала: правила сложения, умножения, вычитания и деления в двоичной системе счисления.
Ход урока.
Изучение нового материала.
Правила сложения:
0+0=0
0+1=1
1+0=1
1+1=10
Обратить внимание учащихся на то, что при сложении двух единиц в двоичной системе счисления в записи получается 0, а единица переносится в следующий разряд. При сложении трех единиц получается в записи 1, и единица переносится в следующий разряд. (1+1+1=11).
Пример 1.
101+10=111
Решение:
+ |
1 |
0 |
1 |
|
1 |
0 |
|
|
1 |
1 |
1 |
Пример 2.
10011+11=1110
Решение:
|
|
1 |
1 |
|
+ |
1 |
0 |
1 |
1 |
|
|
1 |
1 |
|
|
1 |
1 |
1 |
0 |
Учащиеся самостоятельно решают следующие примеры:
1001+11=1100
110+110=1100
Правила умножения:
0*0=0
0*1=0
1*0=0
1*1=1
Пример 1.
101*11=1111
Решение:
* |
1 |
0 |
1 |
|
1 |
1 |
|
|
1 |
0 |
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
Объяснение:
Каждую цифру второго множителя умножаем на каждую цифру первого множителя, результаты произведений складывают между собой по правилам сложения в двоичной системе счисления. (Математика - 3 класс).
Пример 2.
1011*101=110111
Решение:
|
* |
1 |
0 |
1 |
1 |
|
|
1 |
0 |
1 |
|
|
|
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
|
|
1 |
1 |
0 |
1 |
1 |
1 |
Учащиеся самостоятельно решают следующие примеры:
1001*101=101101
1001*11=11011
Правила вычитания:
0-0=0
1-0=1
1-1=0
0-1=-1
Обратить внимание учащихся на то, что «минус» в последнем правиле обозначает – «занять разряд (1)».
Пример 1.
10110-111=1111
Решение:
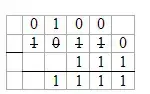
Объяснение:
Вычитание выполняется так же, как в математике. Если цифра в уменьшаемом меньше цифры вычитаемого, то для данного вычитания необходимо занять разряд (1), т.к. 10-1=1. Если слева от такого вычитания стоит 0, то мы не можем занять разряд. В этом случае разряд занимаем в уменьшаемом у близстоящей слева от данного вычитания единицы. При этом все нули, у которых мы не могли занять разряд, необходимо поменять на единицу, т.к. 0-1=-1. Желательно все изменения в цифрах записывать сверху данного вычитания. Дальнейшее вычитание выполнять с получившимися сверху цифрами.
Пример 2.
100000-11=11101
Решение:
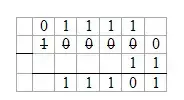
Учащиеся самостоятельно решают следующие примеры:
100010-100=
101011-10111=
Правило деления:
Деление выполняется по правилам математики, не забывая, что мы выполняем действия в двоичной системе счисления.
Пример 1.
101101:1001=101
Решение:
|
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
|
1 |
0 |
0 |
1 |
|
|
1 |
0 |
1 |
|
|
|
|
1 |
0 |
0 |
1 |
|
|
|
|
|
|
|
1 |
0 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
Объяснение:
В частном смело пишем первую 1, т.к. число в двоичной системе не может начинаться с 0. Умножаем эту 1 на делитель, результат правильно записываем под делимом, соблюдая разрядность. Выполняем вычитание по правилам вычитания в двоичной системе счисления. Сносим следующую цифру делимого, и полученное число сравниваем с делителем. В данном случае – полученное число меньше делителя, в частном записываем 0 (в противном случае – 1). Сносим следующую цифру делимого. Получили число равное делителю, в частном записываем 1, и т.д.
Пример 2.
101010:111=110
Решение:
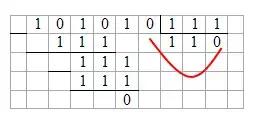
Примеры для самостоятельного решения:
1001000:1000=1001
111100:1010=110
Домашнее задание.
Выполнить действия:
1100+1101=
101+101=
1011*101=
111*101=
11011-110=
10001-1110=
1011010:1010=