Без хорошо продуманных методов обучения трудно организовать усвоение программного материала. Вот почему следует совершенствовать те методы и средства обучения, которые помогают вовлечь учащихся в познавательный поиск, в труд учения: помогают научить учащихся активно, самостоятельно добывать знания, возбуждают их мысль и развивают интерес к предмету.
«Все наши замыслы, все поиски и построения превращаются в прах, если у ученика нет желания учиться.» (В.А.Сухомлинский)
Мотивировать учащихся – значит затронуть их важнейшие интересы и дать им шанс реализоваться в процессе деятельности. Мотивация ответственна за активную жизненную позицию ребенка в обучении и личностном развитии.
При реализации ФГОС каждый ребёнок становится активным субъектом мотивированной сознательной учебной деятельности.
При организации учебной деятельности необходимо ученика вовлечь в процесс самостоятельного поиска и «открытия» новых знаний, решить задачи проблемного характера, что и ведет к раскрытию внутреннего потенциала личности обучающегося. Но, при неправильной организации учебного процесса мотивация снижается. Чтобы процесс мотивации не снижался, необходимо создать условия осмысленности учения, что возможно только с применением различных активных методов, приемов обучения и с включением учащегося в процесс обучения на уровне не только интеллектуальной, но личностной и социальной активности.
Одним из эффективных приемов, способствующих познавательной мотивации, является создание проблемных ситуаций на уроке, когда реализуется исследовательский подход к обучению, смысл которого заключается в том, что ребёнок получает знания не в готовом виде, а «добывает» их в процессе своего труда. Используя системно-деятельностный подход, учитель формирует регулятивные, познавательные, коммуникативные действия.
С целью формирования универсальных учебных действий я применяю педагогические технологии: технологию перспективно-проблемного обучение; модульные технологии; информационно-коммуникативные технологи, технологию развития критического мышления.
В работе использую и новые приемы: «Верные-неверные утверждения», «Прогнозирование», «Знаю – хочу узнать – узнал – научился», «Толстые» и «тонкие» вопросы (Ромашка Блума).
Применяю кластеры, синквейны. Для сочетания элементов различных технологий, создающих комфортную среду урока, использую адаптивный урок.
Реализуя современные технологии через системно-деятельностный подход, работая в технологии моделирования, формирую у школьников умение самостоятельно добывать новые знания, собирать необходимую информацию, делать выводы, умозаключения, т.е. развиваются умения и навыки самостоятельности и саморазвития.
Большой эффект в обучении дает живое слово учителя в сочетании с наглядностью. Здесь уместно вспомнить слова Иога́нна Карла Фри́дриха Гаусса о том, что «математика – наука для глаз, а не для ушей». Разумное использование в учебном процессе наглядных средств обучения играет важную роль в развитии наблюдательности, внимания, речи, мышления. Сейчас это уже не схемы, таблицы и картинки, а ставшая доступной для нас мультимедиа. Такие мультимедийные инструменты, как слайд, презентация способствуют развитию мотивации, коммуникативных способностей, получению навыков, развитию информационной грамотности. ИКТ позволяют развивать интеллектуальные и творческие способности учащихся. Подача учебного материала в виде мультимедийной презентации сокращает время обучения, вызывает интерес, представляя учебный материал в красках, со звуком и другими эффектами, более качественно.
И еще один из моментов повышения мотивации, который, на мой взгляд, вызывает познавательный интерес. Это исторический аспект школьных знаний. Французский математик, физик и философ Жуль Анри Пуанкаре отмечал, что «всякое обучение становится ярче, богаче от каждого соприкосновения с историей изучаемого предмета». Чтобы у учащихся не возникло представление, что математика – наука безымянная, знакомлю их с именами людей, творивших эту науку, богатыми эпизодами их жизни.
Теперь перейдем непосредственно к урокам математики. «Предмет математики настолько серьезен, что нужно не упускать случая делать его немного занимательным» (французский ученый Блез Паскаль). Чтобы процесс обучения был эффективным и интересным, на каждом этапе урока я использую различные методы и приемы активизации. Итак, обо всем по порядку…
Для организации самооценки на протяжении всего урока можно использовать «Линейку достижений». Каждое задание на уроке имеет свое количество баллов, за верное выполнение задания ученик самостоятельно передвигает свою звезду по этой линейке и в конце урока наглядно видно достижение каждого обучающегося отдельно и всего класса в целом.
Этап урока: Мотивация учебной деятельности учащихся
«Смотреть – не значит видеть!»
28k + 30n + 31m = 365 (Задание для учащихся: к концу урока мы должны найти с вами хотя бы одно решение этого уравнения).
Игра «Знаете ли вы, что…?» - эффективный прием, помогающий настроить учащихся на работу, заинтересовать изучаемой темой.
- Знаете ли вы, что Л.Н.Толстой, автор романа «Война и мир», писал учебники для начальной школы и, в частности, учебник арифметики?
- Знаете ли вы, что все современные учебники по геометрии составлены на основе известных «Начал» Евклида (IV в. до н. э.)?
- Знаете ли вы, что великий русский поэт М.Ю.Лермонтов интересовался математикой и мог до поздней ночи решать какую-нибудь математическую задачу?
- Знаете ли вы, что Пифагор был победителем кулачного боя на 58-х Олимпийских играх, проходивших в 548 году до н. э., а затем побеждал еще на нескольких Олимпиадах?
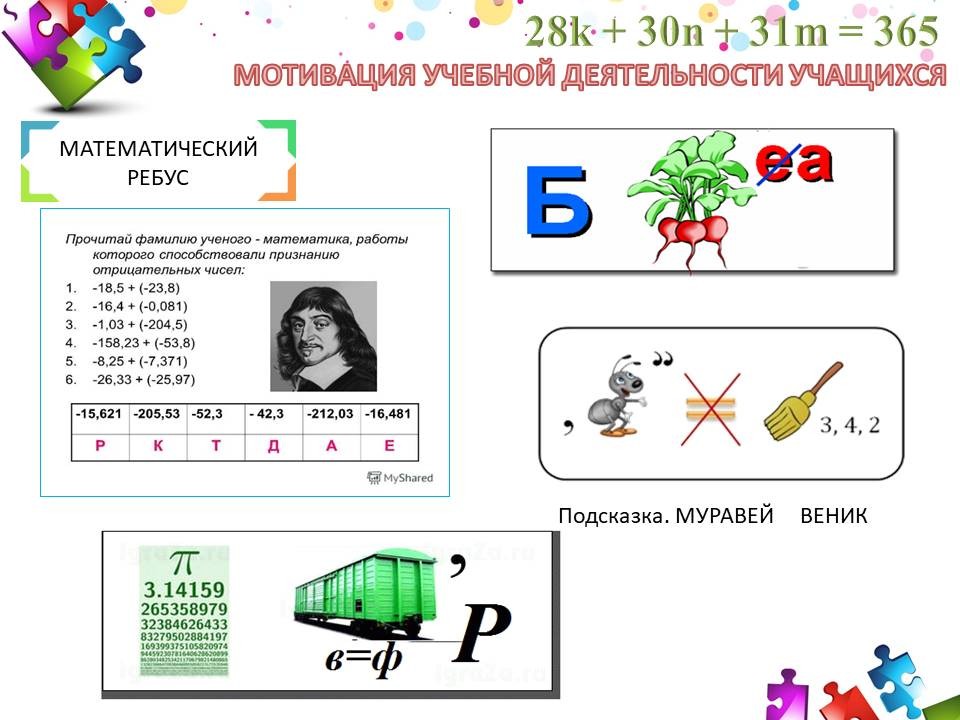
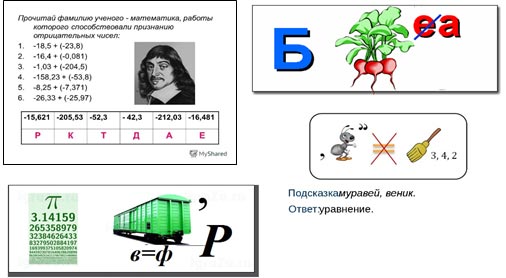
- Разгадав математический ребус, ребята узнают фамилию известного ученого математика, новое математическое понятие.
Этапа урока: Проверка домашнего задания, воспроизведение и коррекция знаний, навыков и умений учащихся
«Тонкие» и «Толстые» вопросы
«Тонкими» называют простые, односложные вопросы, требующие ответа да/нет. «Толстые» вопросы выводят учеников на более высокий уровень мышления: сравнение, анализ, синтез, оценку.
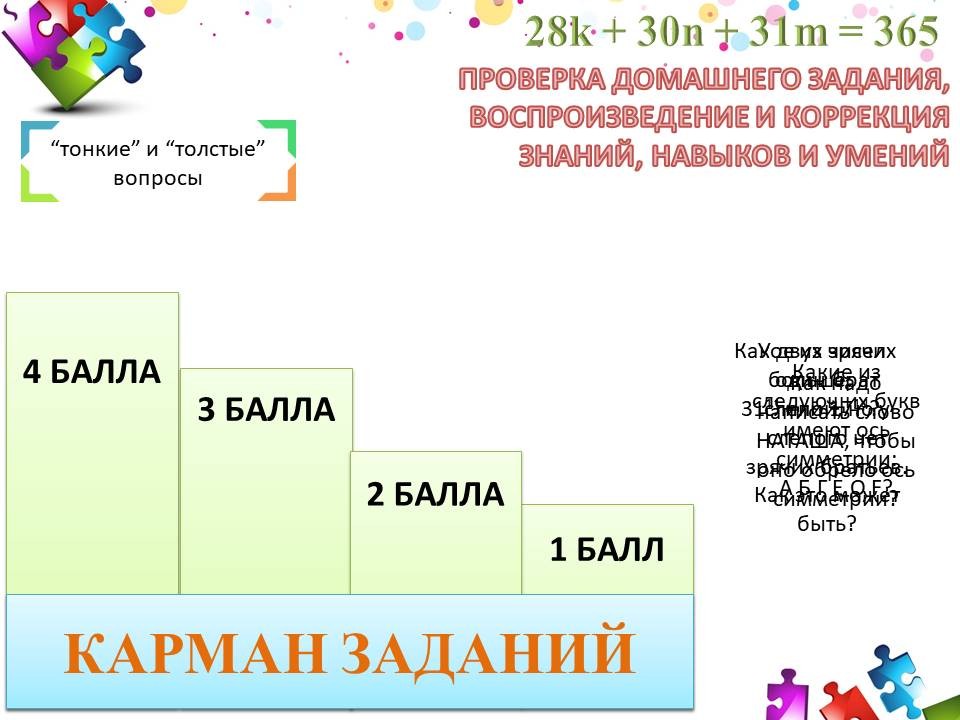
«Толстые» вопросы можно организовать в форме “Карман с заданиями” (пример на слайде). Каждый вопрос имеет свой балл для самооценки по «Линейки достижений».
1 балл.
- 5-й класс. Какие из следующих букв имеют ось симметрии: А, Б, Г, Е, О, F?
2 балла.
- 7-й класс. Как надо написать слово НАТАША, чтобы оно обрело ось симметрии.
Эта задача на сообразительность, она помогает диагностировать уровень развития пространственного мышления каждого школьника.
3 балла.
- 6-й класс. У двух зрячих один брат слепой, но у слепого нет зрячих братьев. Как это может быть?
Ответ: из первой фразы как будто следует, что речь в задаче идет о братьях, тогда как на самом деле зрячими оказываются сестры).
4 балла.
- 8-й класс. Какое из чисел больше: 3111 или 1714?
Подсказка. Сравните эти числа со степенями двойки.
Решение: Имеем: 3111 < 3211 = 255 < 256 = 1614 < 1714.
Ответ: второе число больше.
Теорема – пазл
Учащимся предлагается собрать теорему из 4 фрагментов. На одном содержится формулировка теорем, на другом – чертеж к теореме, на третьем - что дано и что требуется доказать, на четвертом - доказательство. Все теоремы темы (курса) собраны в одном пакете.
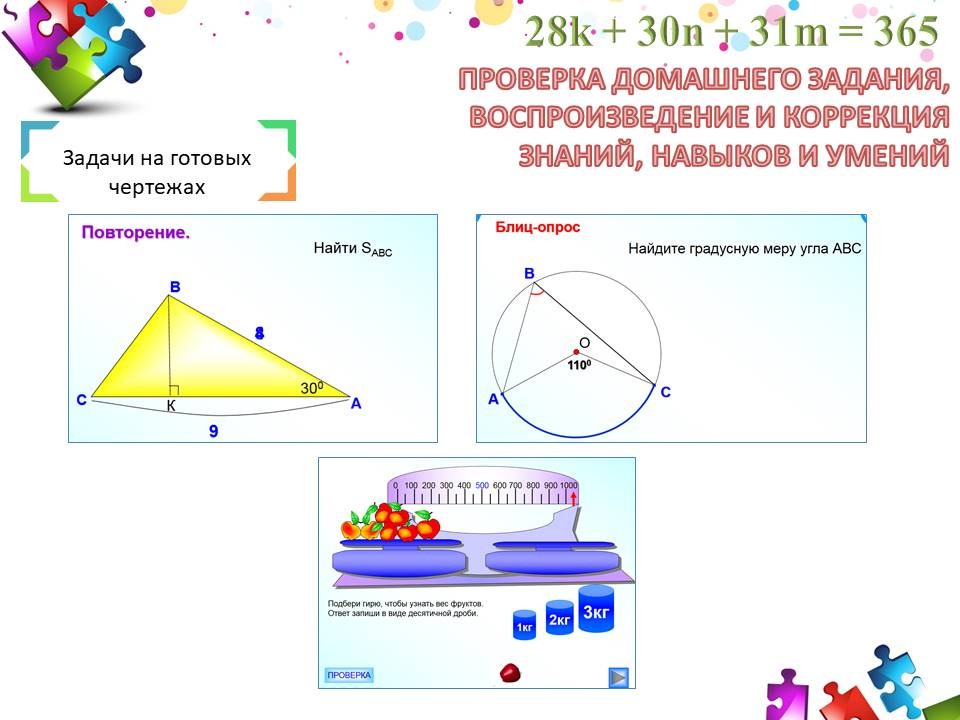
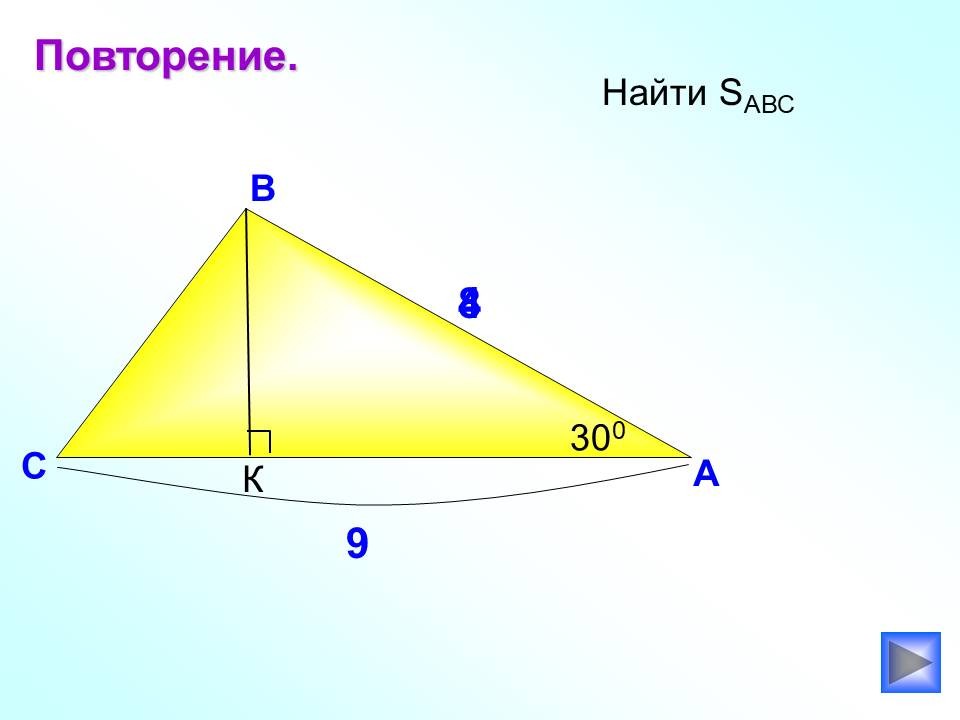
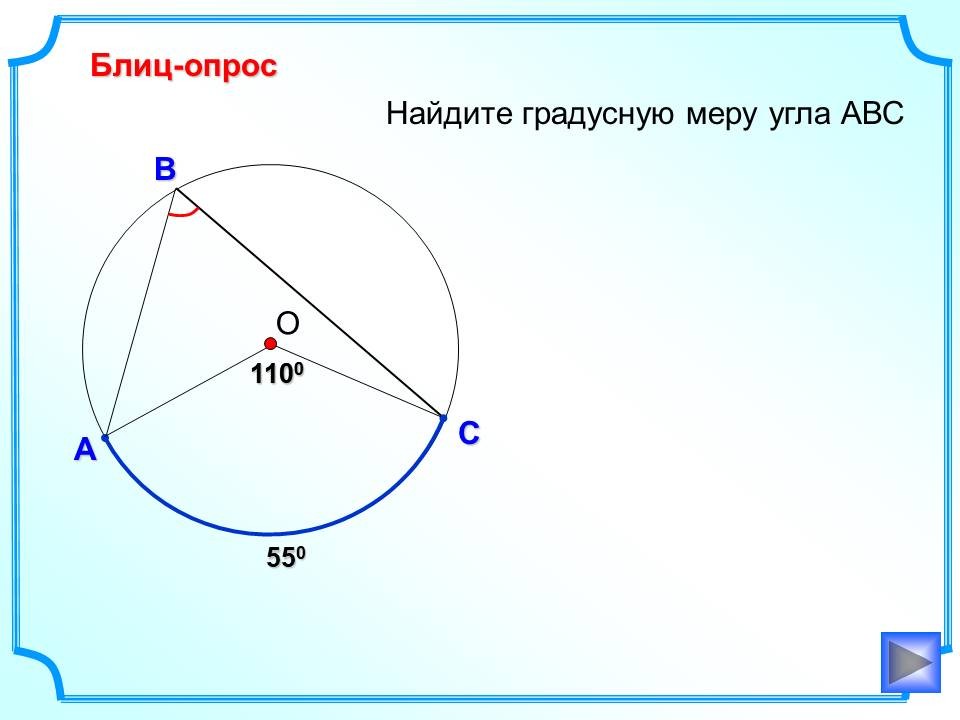
Задачи на готовых чертежах
Такие задачи позволяют увеличить темп работы на уроке, так как данные задачи находятся перед глазами на протяжении всего решения; активируют мыслительную деятельность учащихся; помогают запомнить теоретический материал.
Этап урока. Актуализация знаний
«Немой» вопрос
Организация сценки «Закон сложения». Угадать, что продемонстрировано.
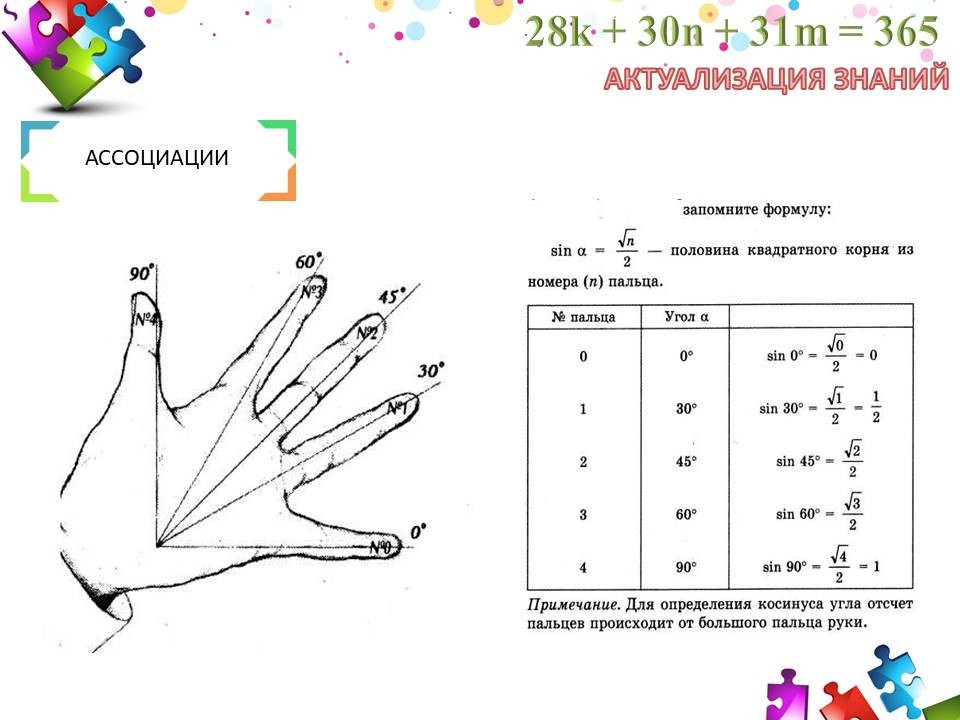
Ассоциации вместо правил
Привлекают внимание учащихся и поддерживают их познавательную деятельность. Например, для лучшего запоминания значений тригонометрических функций на уроках геометрии знакомлю учащихся 8 класса с «Тригонометрией в ладони».
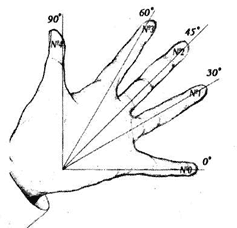
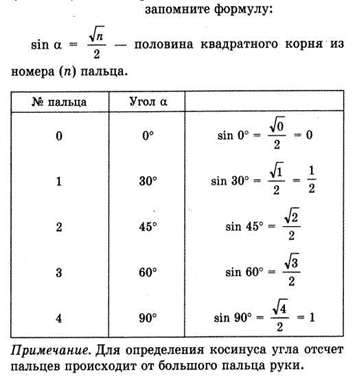
- Ребята, оказывается, значения синусов и косинусов углов «находятся» на вашей ладони. Как будет представлена схема для косинусов данных углов на ладони?
Задачи с занимательным сюжетом или задачи – шутки
8-й класс. Тема “Длинна окружности”.
Представьте себе, что вы охватили земной шар по экватору. А теперь прибавьте к длине окружности 1 метр и снова охватите земной шар, у вас должен получиться зазор. Пролезет ли кошка через этот зазор?
Решение:
Такие нестандартные задачи у учащихся вызывают большой интерес. На первый взгляд, кажется, что ответ должен быть отрицательным, но если задачу перевести на язык геометрии, то нужно найти всего лишь разность между радиусами двух окружностей.
Пусть С – длина окружности, тогда (С +1) – длина большей окружности. Радиус первой окружности равен ![]() , радиус большей окружности равен
, радиус большей окружности равен ![]()
Тогда величина зазора равна: ![]() .
.
Сложить газету 50 раз.
1 слой приблизительно равен 2мм. Тогда получаем ![]() , что составляет 4-5 раз от Земли до Луны!
, что составляет 4-5 раз от Земли до Луны!
Прием «Использование знаний математики на других уроках»
При изучении геометрии очень много возможностей применить знания на практике:
- параллельные прямые: покраска стен бордюром параллельно полу, провешивание прямой при подготовке клумб к посадке, посадка бордюрных кустов перед школой.
- перпендикулярные прямые: измерения длины комнаты и количество рулонов обоев для ремонта классной комнаты. Перпендикулярность их к полу и потолку.
- измерение площади классной комнаты для покупки линолеума.
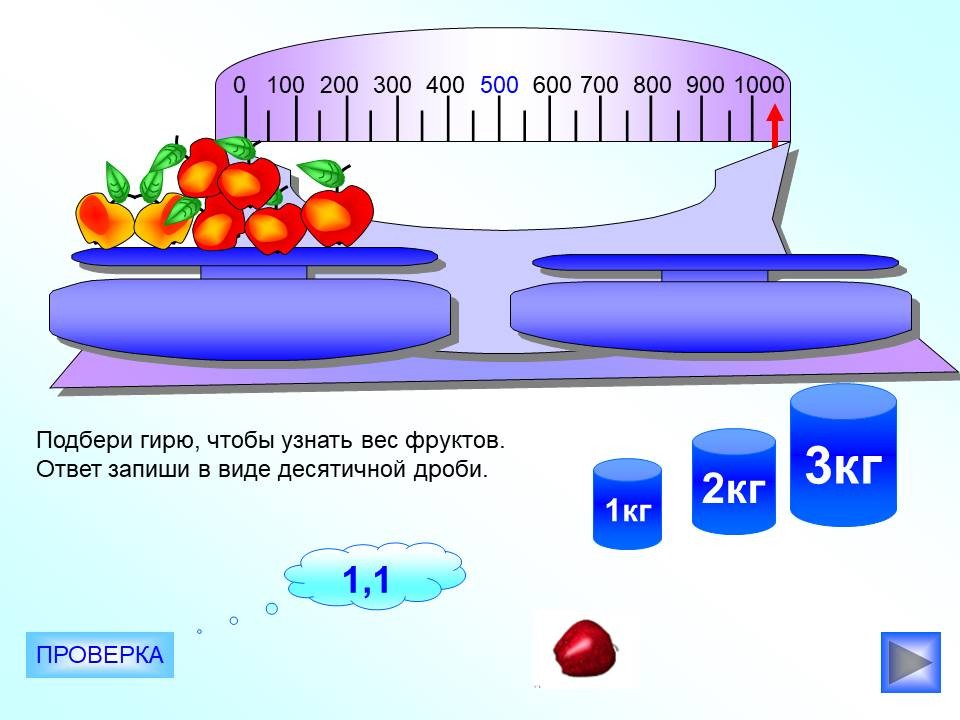
В старших классах дети понимают, что огромное количество информации нам подаётся в процентах и мы брали газеты и находили много материала для задач:
«Процентные вычисления в жизненных ситуациях»
Решение задач на темы:
1. Распродажа.
2. Тарифы.
3. Штрафы.
4. Банковские операции.
5. Голосование.
Основная цель: показать широту применения в жизни такого простого и известного учащимся математического аппарата, как процентные вычисления.
Координаты. В географии и в жизни человека.
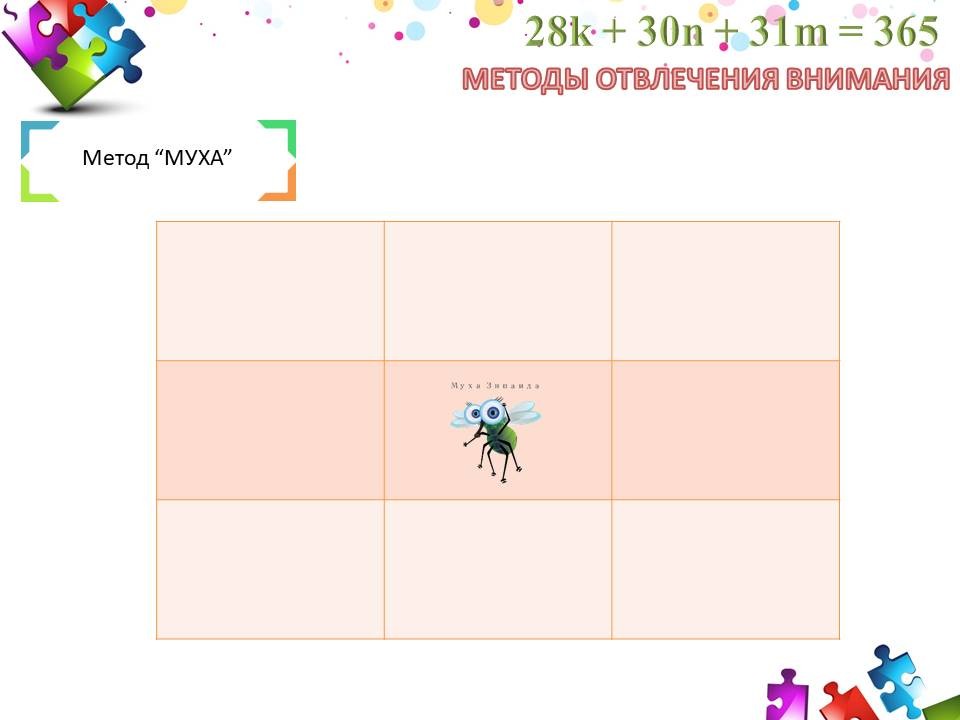
Если обучающиеся устали, а впереди еще много работы или сложная задача, следует сделать паузу и прибегнуть к методам отвлечения внимания. Иногда достаточно 5 минут веселой и активной игры для того, чтобы встряхнуться, весело и активно расслабиться, восстановить энергию. Активные методы «Постройся по росту», «Пантомима», «Муха» и многие другие позволят это сделать, не выходя из класса.
Метод «Муха». На доске нарисовано поле 3х3. В центре «сидит муха». «Муха» может перемещаться вверх, вниз, влево, вправо. Участники по очереди отдают команды и следят за положением воображаемой «мухи». Тот, кто выведет муху за пределы поля, выбывает.
Этап урока. Первичное закрепление
В качестве закрепления нового материала успешно применяется игра «Да» - «Нет». Вопрос читается один раз, переспрашивать нельзя, за время чтения вопроса необходимо записать ответ «да» или «нет». Главное здесь – приобщить даже самых пассивных к учёбе.
Например, на уроке геометрии в 8 классе по теме «Четырехугольники» можно использовать такие вопросы.
- У прямоугольника смежные стороны перпендикулярны!
- В любой прямоугольник можно вписать окружность!
- Квадрат является прямоугольником!
- Любой прямоугольник является ромбом!
- Диагонали прямоугольника равны!
- Диагонали прямоугольника взаимно перпендикулярны!
- Диагонали прямоугольника делятся точкой пересечения пополам!
- Диагонали прямоугольника являются биссектрисами его углов!
Утверждения, с которыми либо соглашаются, либо не соглашаются, ученики готовят сами в качестве дополнения к домашнему заданию на протяжении изучения всей темы.
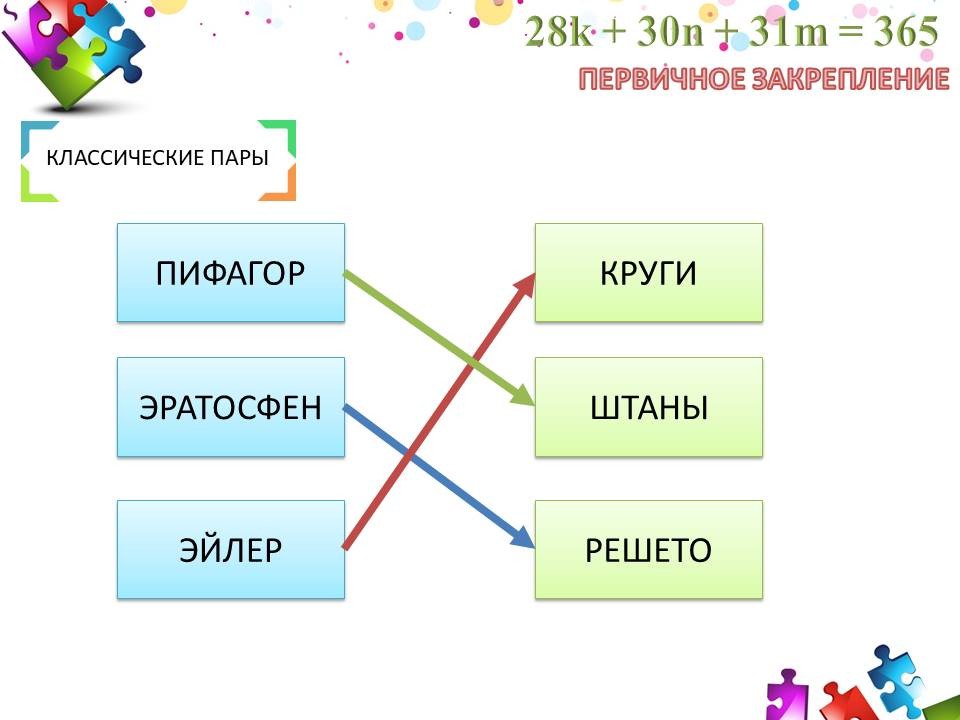
Метод «Классические пары»
На карточках написаны понятия и фамилии людей, имеющие связь между собой. Учащиеся должны найти и составить «классическую пару».
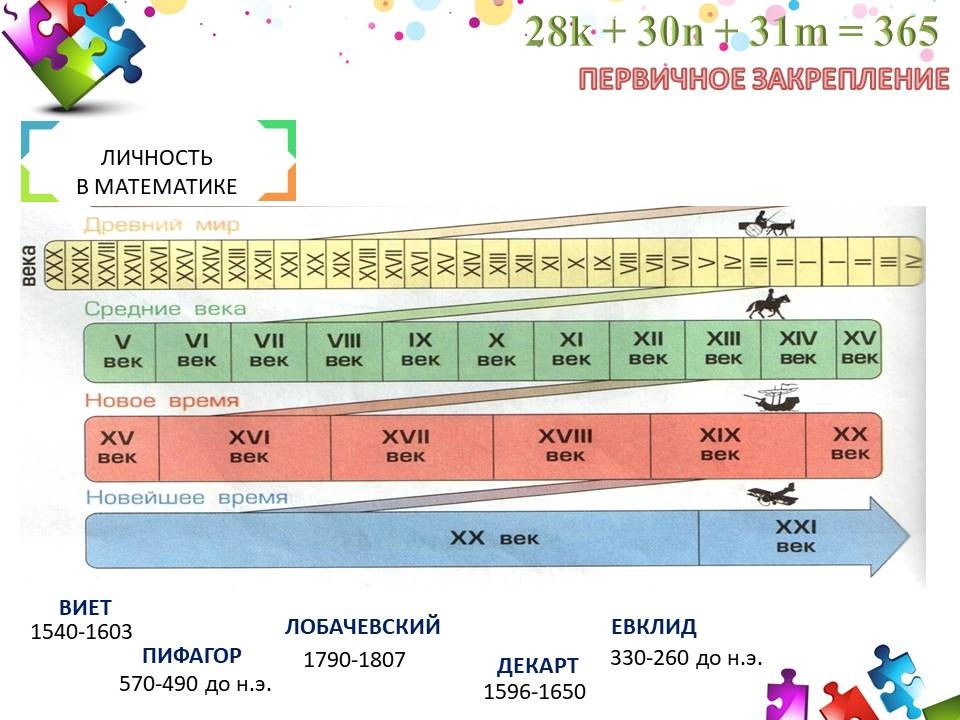
Использование метода «Личность в математике» подталкивает обучающихся к самостоятельному поиску информации. Группе из 3-4 человек дается лист ватмана с изображенной на ней «лестницей эволюции» с историческими ступеньками. Задача: разместить на этой лестнице в хронологическом порядке по годам жизни ученых-математиков: например, Виет, Пифагор, Герон, Лобачевский, Декарт, Евклид и т.д. У каждой ступеньки написать век или года жизни и рассказать, чем знаменит ученый.
Этап урока. Итог занятия
Вернемся к эмблеме занятия.
28k + 30n + 31m = 365
Кто увидел? Кто догадался? Кто решил?
“Смотреть – не значит видеть!”
Ответ: 365 – это количество дней в году, 28 – количество дней в феврале, 30 – количество дней имеют 4 месяца в году, 31 – количество дней имеют 7 месяцев в году. Тогда: 28 ·1 + 30 · 4 + 31 · 7 = 365.
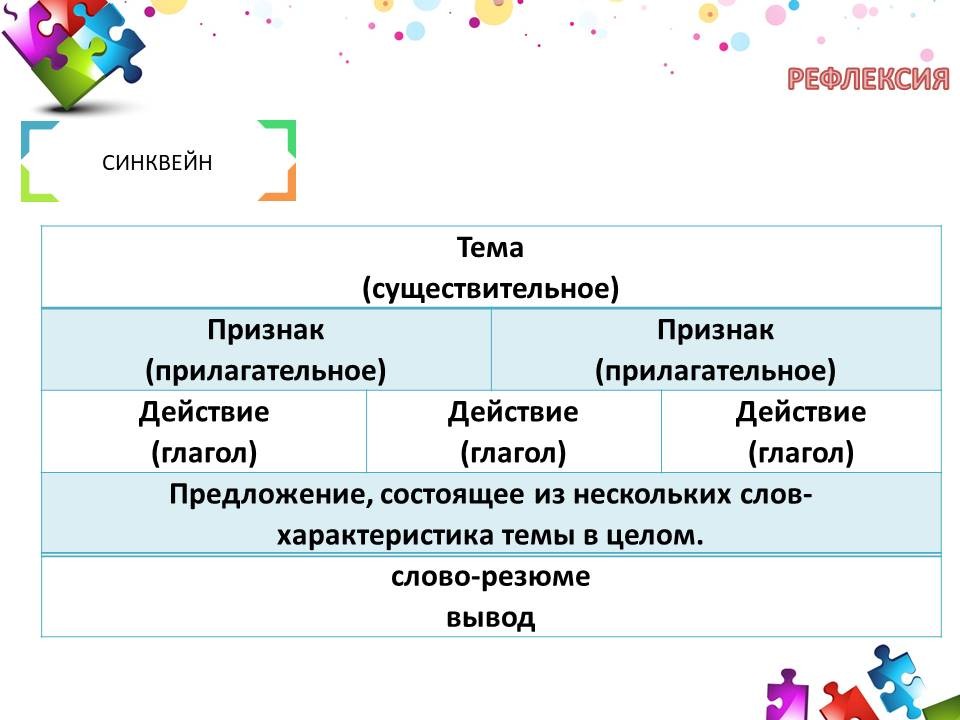
Этап урока. Рефлексия
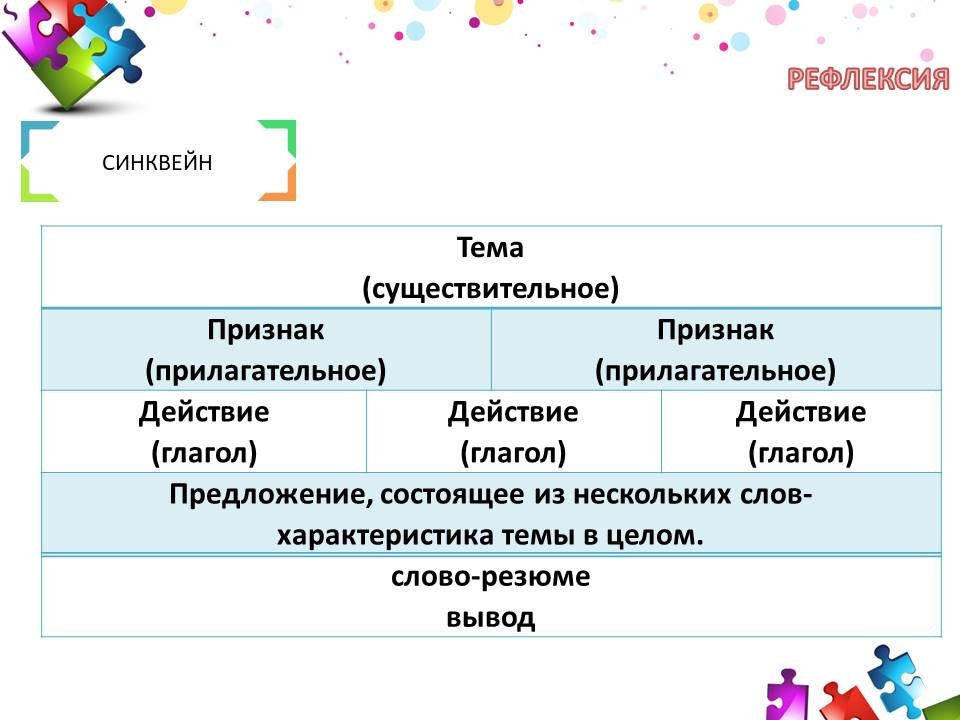
Синквейн
Тема (существительное) |
|||
Признак (прилагательное) |
Признак (прилагательное) |
||
Действие (глагол) |
Действие (глагол) |
Действие (глагол) |
|
Предложение, состоящее из нескольких слов- |
|||
Слово-резюме |
|||
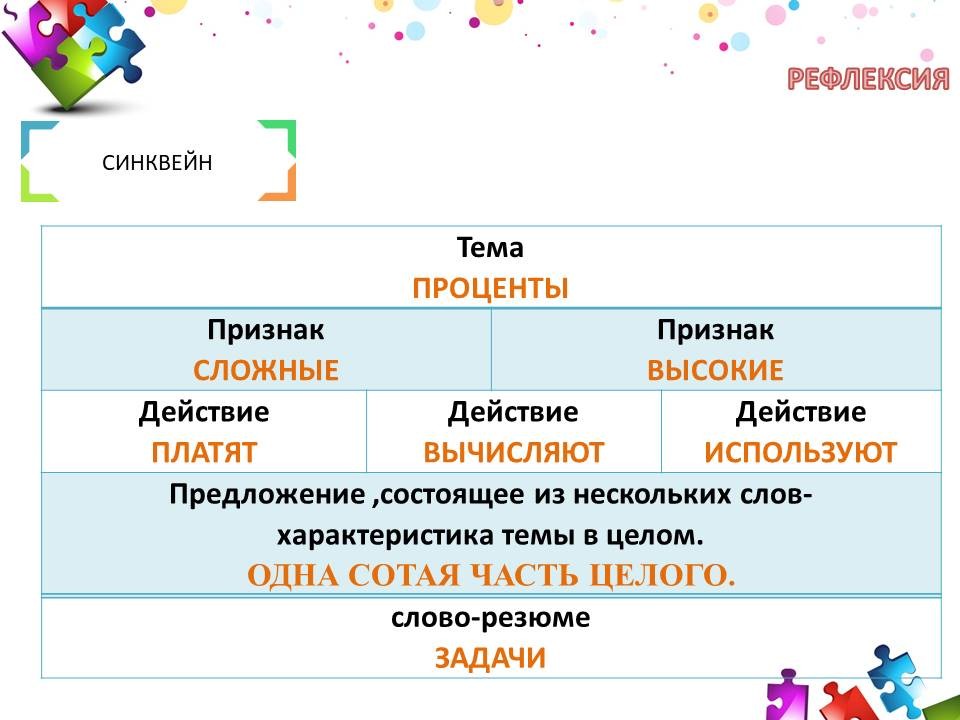
Пример синквйна по теме «проценты»:
Проценты
Сложные Высокие
Платят вычисляют Используют
Одна сотая часть целого.
Задачи
- Составить синквейн мастер-класса.
СПАСИБО ЗА ВНИМАНИЕ!