I. Немного о изложении метода интервалов в школьном курсе
Анализ учебной литературы, личный опыт, опыт коллег, итоги ГИА и ЕГЭ позволяют судить о недостаточной проработке метода интервалов с точки зрения методики, о неполном понимании некоторыми учителями математики сути метода интервалов и (чего уже стесняться) иногда о не владении методом интервалов отдельно взятыми учителями, о слабом представлении обучащимися об использовании этого метода в дальнейшем.
Приведу наиболее удачный, на мой взгляд, пример изложения метода интервалов:
Алгебра: учеб. Для учащихся 9 кл. с углубл. Изучением математики/[Н. Я. Виленкин, Г. С. Сурвилло, А. С. Симонов, А. И. Кудрявцев]; под ред. Н. Я. Виленкина. – 6-е изд., дораб. – М.: Просвещение, 2005. – 367 с.
Стр. 196
Всякий многочлен P(x), имеющий корнями числа a1, a2, a3, ... , an может быть представлен в виде P(x) = (x – a1)(x – a2)(x – a3) ... (x – an) . Q(x) неравенство P(x) > 0 можно записать так: (x – a1)(x – a2)(x – a3) ... (x – an) . Q(x) > 0 (*). При этом если a1, a2, a3, ... , an – все корни многочлена P(x), то многочлен Q(x) корней не имеет и, следовательно, сохраняет один и тот же знак на всей числовой оси.
Каждый из линейных множителей x – ak положителен
при x > ak и отрицателен при x
< ak. Значит, произведение,
стоящее в левой части неравенства (*), может
изменить знак лишь при переходе переменной x через
одну из точек ak. Точки ak делят
числовую ось на несколько интервалов, на каждом
из которых рассматриваемое произведение знака
не меняет. Отсюда следует, что достаточно знать
знак произведения в какой-нибудь одной
(«пробной») точке внутри интервала, и этот же знак
будет иметь произведение во всех точках данного
интервала.
Рассмотренный метод решения неравенств назвали методом
интервалов. Вы его использовали при решении
квадратных неравенств в 8 классе.
Итак, чтобы решить целое рациональное
неравенство, используя метод интервалов, нужно:
Алгоритм:
1) перенести все слагаемые в левую часть и
решить уравнение, приравняв выражение в левой
части к нулю;
2) найденные корни уравнения нанести на числовую
ось. Эти корни разбивают числовую ось на
промежутки, на каждом из которых выражение,
стоящее в левой части, сохраняет знак;
3) выбрать в каждом из промежутков какое-нибудь
значение («пробную» точку) и определить знак
выражения в этой точке;
4) выбрать промежутки, в которых выражение имеет
требуемый знак, записать ответ, взяв их в
объединение
При рассмотрении примера 1 в учебнике типа (x – 1)2(x + 1 )(x – 3) < 0 предлагается выбирать «пробную» точку в каждом интервале. О кратности корней многочлена речи вообще нет. О ней вскользь упоминается в конце параграфа, но отсутствуют указания, что делать школьнику в этом случае.
В следующем параграфе «Решение дробно-рациональных неравенств» нет речи ни о методе интервалов, ни об области допустимых значений дробно-рациональной функции. Точки, «полученные из знаменателя» отмечены так же как и точки, «полученные из числителя». «Разобраны» два примера и все.
Примерно так же метод интервалов излагается и в учебнике Алгебра: Учеб. Для 9 кл. общеобразоват. учреждений./С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин. – 2-е изд. – М.: Просвещение, 2003. – 255 с. Стр. 34-35, но алгоритм уже не формулируется.
В остальных учебниках, просмотренных мною для выполнения этого задания (
Учебники математики материал по методу
интервалов излагают недостаточно полно, и
опытные педагоги стараются расширить его в
10-11классах, но на это уходит дополнительное
время, а иногда оказывается, что и расширять
нечего, так как нужно обучать десятиклассников
методу интервалов заново.
В своей работе мне довелось обучать методу
интервалов несколькими способами, но наиболее
эффективным, удобным и доступным для
обучающихся, с моей точки зрения, является
алгоритм обобщенного метода интервалов. Он
подходит для обучения детей с различным уровнем
математической подготовки и для профильного в
том числе, в чем не раз убеждалась на практике.
Упоминаю об этом именно потому, что несмотря на то, что выполняю задание по составлению системы задач по теме «метод интервалов», «работая» по учебнику Мордковича или Виленкина, опираюсь все равно на алгоритм обобщенного метода интервалов.
II. Система задач по обучению обобщенному методу интервалов с использованием алгоритма
Урок проводится в 9 классе и является первым уроком, на котором предлагается решение неравенств, отличных от линейных. В 8 классе, конечно, были квадратные неравенства и можно начать урок с повторения, решив одно-два квадратных неравенства, но я это сделала, допустим, на предыдущем занятии, а в этот момент у меня цель другая.
Итак:
№ 1. Устный счет
Цель: подготовка обучащихся к восприятию нового материала.
Рассматриваются примеры, которые позволяют сделать выводы относительно выражений, которые не влияют на знак неравенства, но существенно влияют на решение неравенства.
1)
В ходе решения обучащихся нужно подвести к следующему выводу: выражение, стоящее в четной степени, не влияет на знак неравенства, но влияет на решение и «отбрасывать» его без дополнительных ограничений нельзя.
2) Рассмотрим решение неравенства ![]()
Делается акцент на то, что выражение (x + 3) также не влияет на знак неравенства, но не учитывать его нельзя, иначе решение будет неверным.
![]() , на ноль делить
нельзя, сократить хочется, а можно? и т. д.
, на ноль делить
нельзя, сократить хочется, а можно? и т. д.
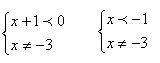
Ответ: ![]() .
.
Данные два случая(выражение в четной степени и выражение, на которое произведено сокращение) отнесем к категории особых случаев и это будет учтено при описании алгоритма.
3) обучащимся даются два выражения: ![]() и a . b и
предлагается рассмотреть знак обоих выражений в
следующих случаях:
и a . b и
предлагается рассмотреть знак обоих выражений в
следующих случаях:
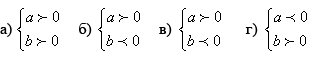
Вывод, который должны сделать обучащиеся: знак частного совпадает со знаком произведения. Это позволит в дальнейшем не переходить от частного к произведению. Обычно при этом переходе и происходит потеря знаменателя вообще.
После данной работы переходим к работе с графиками функций.
Рассматривая рисунок 1, учащиеся должны ответить на вопрос: «Когда происходит смена знака функции?»
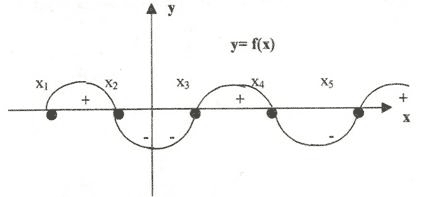
Рис. 1
Ответ: при переходе функции через нуль.
Это же самое подтверждается и рисунком 2.
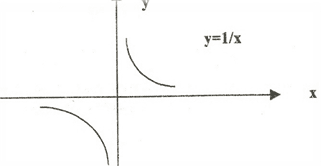
Рис.2
Рассмотрим теперь рисунок 3.
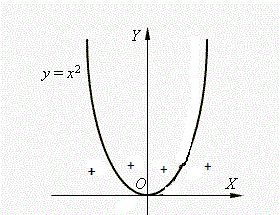
Рис. 3
Хотя точка x = 0 является нулем функции, но функция при переходе через нуль знак не меняет. Данная функция относится к категории особых случаев и, так как четная степень функции не влияет на знак неравенства, перемены знака нет.
При рассмотрении рисунка 4 обращаем внимание на то, что x = 0 не является нулем функции, но при переходе через нуль знак функции меняется. Это говорит о том, что те точки, которые обращают в нуль знаменатель( точки разрыва) тоже должны быть учтены как точки, при переходе через которые функция меняет свой знак.
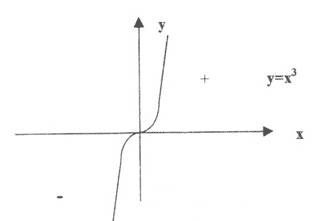
Рис. 4
После проделанной устной работы записываем алгоритм метода интервалов, который позволяет даже детям с недостаточной математической подготовкой решать достаточно сложные неравенства. Параллельно записи алгоритма разбирается пример, причем при объяснении не обязательно идти от простого к сложному, а наоборот, от сложного безболезненно можно переходить к решению простейших неравенств. Лучше даже для первого введения алгоритма подобрать пример максимально исчерпывающий возможные ситуации по алгоритму.
При записи конспекта в тетрадь с обучающимся рекомендую разделить лист тетради на две колонки: в одной записывать алгоритм, а в другой – пример, но непросто так, а каждому шагу алгоритма в одной колонке ставить в соответствие действие по решению неравенства. Таким образом, мы приступаем к решению задачи № 2.
Цель: ввести алгоритм, формировать представления о применении алгоритма.
Решить неравенство:
![]()
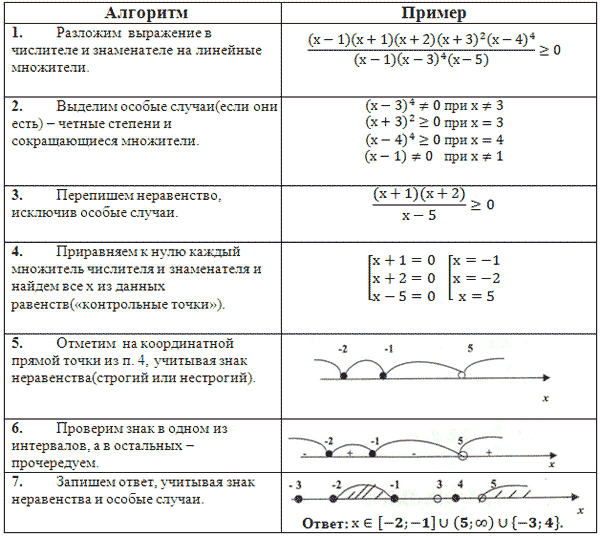
После изучения алгоритма полезно рассмотреть следующие примеры:
Задача №3
Цель: закрепление применения алгоритма, рассмотрение контрпримеров на некоторые шаги алгоритма.
1. ![]() (ситуация
«трудная» или неожиданно «необычная» для многих
детей, когда «вдруг» квадратный трехчлен не
раскладывается на множители).
(ситуация
«трудная» или неожиданно «необычная» для многих
детей, когда «вдруг» квадратный трехчлен не
раскладывается на множители).
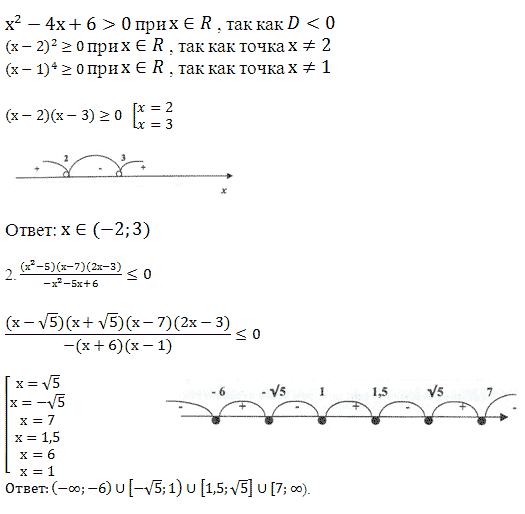
Задача №4. Применение метода интервалов при раскрытии модуля
Цель: расширить представления школьников о применении метода интервалов (внутрипредметные связи).
Решим уравнение: | x – 2 | + | x – 1 | – | x – 5 | = 2x + 3
Для того, чтобы раскрыть модуль, необходимо знать, когда выражение под знаком модуля принимает положительные значения, а когда отрицательные. Но мы знаем, что выражение меняет знак, проходя через нуль, поэтому, на основании изложенного выше, каждое выражение под знаком модуля приравниваем к нулю. Тогда точки, которые обращают в нуль каждое выражение, разобьют координатную прямую на несколько интервалов. Для каждого из промежутков мы будем иметь соответствующее уравнение после раскрытия модулей.

Литература:
- Алгебра: учеб. для учащихся 9 кл. с углубл. изучением математики/ [ Н. Я. Виленкин, Г. С. Сурвиллоо, А. С. Симонов, А. И. Кудрявцев ]; под ред. Н. Я Виленкина. – 6-е изд., дораб. – М.: Просвещение, 2005. – 367с
- http://900igr.net/kartinki/algebra/Uravnenija.html
- Авторская программа по математике для профильных классов Е. И. Надеждкиной, ИПКРО, 1999 г. Г. Иркутск.