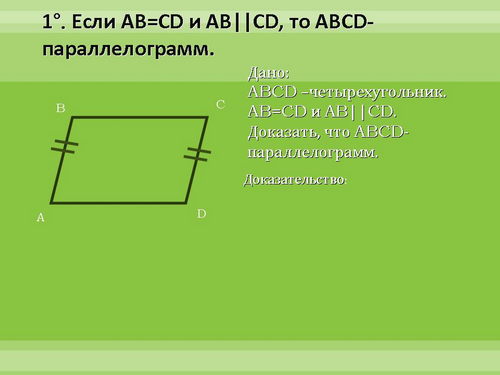
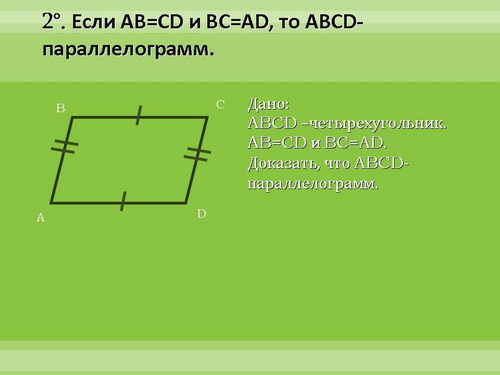
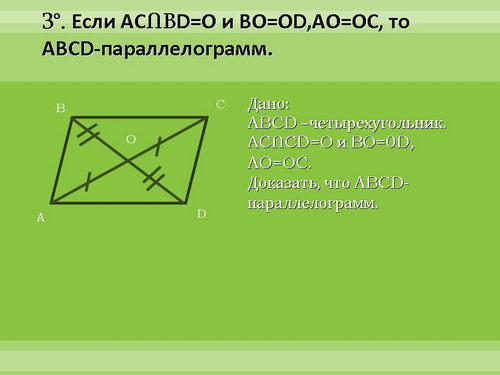
Цель урока: рассмотреть признаки параллелограмма и закрепить полученные знания в процессе решения задач.
Задачи:
- образовательная: формирование умений применять признаки параллелограмма для решения задач;
- развивающая: развитие логического мышления, внимания, навыков самостоятельной работы, навыков самооценки;
- воспитательная: воспитание интереса к предмету, умение работать в коллективе, культуре общения.
Тип урока: изучение нового материала, первичное закрепление.
Оборудование: интерактивная доска, проектор, карточки с заданием, презентация.
Ход урока
1. Организационный момент.
У: Добрый день, ребята! Сегодня на уроке мы опять будем говорить о параллелограмме. Нам предстоит выполнить много заданий, доказать теоремы и научиться применять их при решении задач. Девизом нашего урока будут слова Ле Карбюзье: "Всё вокруг - геометрия".
2. Актуализация знаний учащихся.
Теоретический опрос
Некоторым учащимся дать индивидуальные задания по карточкам на тему свойства параллелограмма (задания выбирает каждый самостоятельно на слайде презентации по гиперссылке, наводя указатель мышки на фигуру, но не на цифру) , выслушать индивидуально каждого отвечающего.

С остальным - доказать дополнительные свойства параллелограмма. (Сначала обсудить устно доказательство, затем сверить с интерактивной доской).
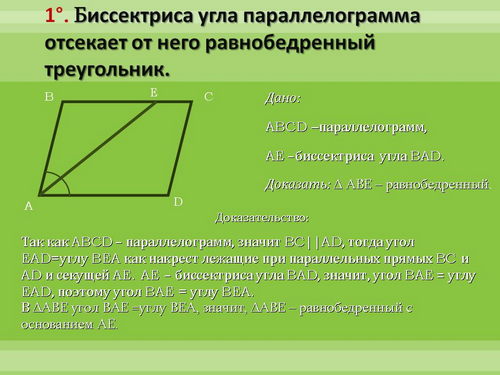
1°. Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.
2°. Биссектрисы соседних углов параллелограмма перпендикулярны, а биссектрисы противоположных углов параллельны или лежат на одной прямой.
После подготовки выслушать доказательства дополнительных свойств параллелограмма.
Дано:
ABCD -параллелограмм,
AE -биссектриса угла BAD.
Доказать: ![]() ABE
- равнобедренный.
ABE
- равнобедренный.
Доказательство:
Так как ABCD - параллелограмм, значит BC || AD, тогда угол EAD = углу BEA как накрест лежащие при параллельных прямых BC и AD и секущей AE. AE - биссектриса угла BAD, значит, угол BAE = углу EAD, поэтому угол BAE = углу BEA.
В ![]() ABE угол BAE =углу
BEA, значит,
ABE угол BAE =углу
BEA, значит, ![]() ABE -
равнобедренный с основанием AE.
ABE -
равнобедренный с основанием AE.
Наводящие вопросы:
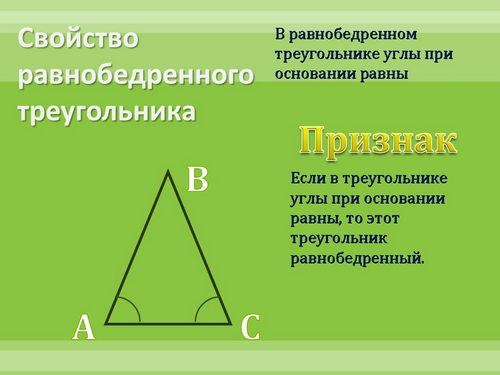
Сформулируйте признак равнобедренного треугольника.
Какие углы в ![]() BAE
могут быть равными? Почему?
BAE
могут быть равными? Почему?
Дано:
ABCD -параллелограмм,
BE -биссектриса угла CBA,
AE - биссектриса угла BAD.
![]()
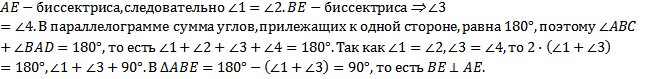
Наводящие вопросы:
Когда прямые AE и CK будут параллельными?
Равны ли углы BEA и <3? Почему?
В каком случае AE и CK совпадут?
Подготовка к изучению нового материала
Фронтальная работа с классом (устно).
- Что означают слова "свойства" и "признак"? Приведите примеры.
- Что такое обратная теорема?
- Всегда ли верно утверждение обратное данному? Приведите примеры.
3. Объяснение нового материала.
У.: У каждого объекта есть свои свойства и признаки. Скажите, пожалуйста, чем отличаются свойства от признаков.
Давайте попробуем разобраться в этом вопросе на простом примере. Дан объект - осень. Назовите его свойства: Его признаки:
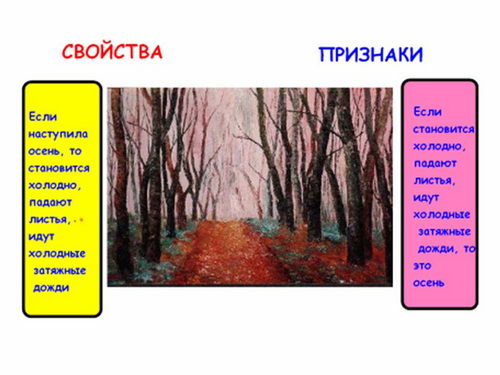
- Какими утверждениями являются по отношению друг к другу свойство и признак объекта? (ответ: обратными)
- Какие свойства в курсе геометрии мы уже изучали? Сформулируйте их. (называют несколько)
Для любого ли свойства можно построить верное обратное утверждение? (разные ответы).
Проверим это на следующих свойствах:
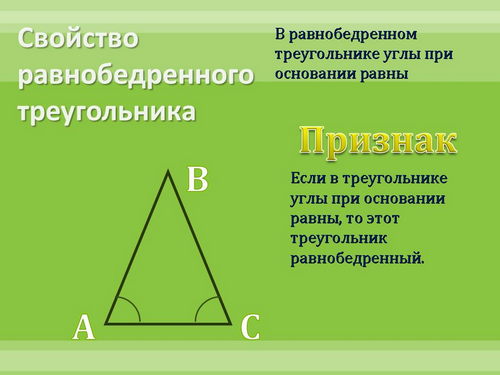
Сделайте вывод: Для любого ли свойства можно построить верное обратное утверждение? (нет, не для любого)
Теперь, давайте вернёмся к нашему четырёхугольнику, вспомним его свойства и сформулируем обратные для них утверждения, т.е:.. (ответ - признаки параллелограмма). Итак, тема сегодняшнего урока: "Признаки параллелограмма".
Итак, назовите свойства параллелограмма.
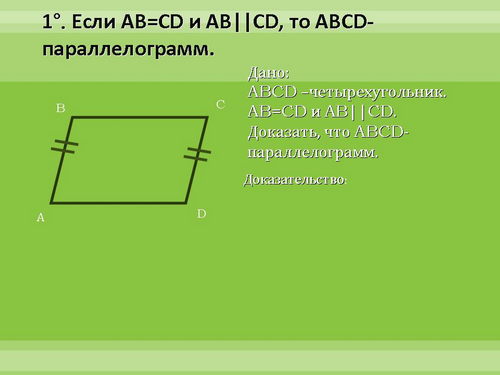
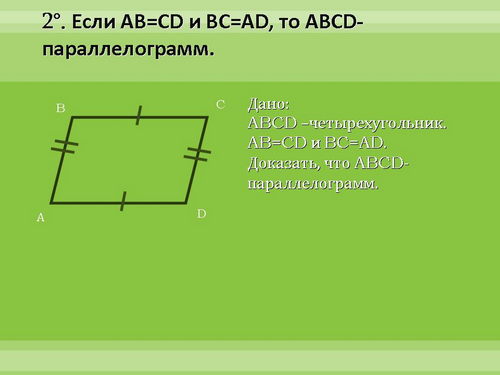
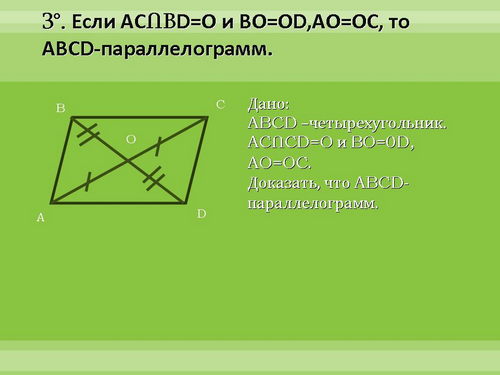
Сформулируйте обратные свойствам утверждения. (ученики формулируют признаки, учитель их корректирует и формулирует повторно)
Докажем, эти признаки. Первый признак - подробно, второй - коротко, третий - самостоятельно дома.

4. Закрепление изученного материала.
Работа в рабочих тетрадях: решить задачу №11 на интерактивной доске к доске вызвать менее подготовленного учащегося.
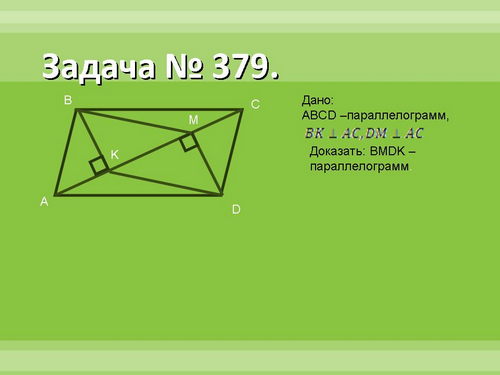
Решение задачи № 379 (решение записать на
интерактивной доске). Из вершин B и D
параллелограмма ABCD, у которого AB ![]() BC и
BC и ![]() А
острый, проведены перпендикуляры ВК и DМ к прямой
АС. Докажите, что четырёхугольник BMDK -
параллелограмм.
А
острый, проведены перпендикуляры ВК и DМ к прямой
АС. Докажите, что четырёхугольник BMDK -
параллелограмм.
Даю время ученикам, чтобы подготовили чертёж.
Дано: ABCD - параллелограмм, BK![]() AC, DM
AC, DM![]()
Доказать, что: BMDK - параллелограмм.
Доказательство:
![]() BKC=
BKC= ![]() DMA по гипотенузе и острому углу (
DMA по гипотенузе и острому углу (![]() как
накрест лежащие углы при параллельных прямых AD и
BC и секущей AC, BC=AD как противолежащие стороны
параллелограмма,
как
накрест лежащие углы при параллельных прямых AD и
BC и секущей AC, BC=AD как противолежащие стороны
параллелограмма, ![]() BKC и
BKC и ![]() DMA
прямоугольные), значит MD=BK.
DMA
прямоугольные), значит MD=BK.
![]() BMK и
BMK и ![]() DKM - прямоугольные,
DKM - прямоугольные, ![]() BMK
=
BMK
= ![]() DKM по двум катетам (MD=BK, KM-
общий катет), значит BM=DK.
DKM по двум катетам (MD=BK, KM-
общий катет), значит BM=DK.
В четырехугольнике BMDK противолежащие стороны равны (MD=BK и BM=DK), следовательно, BMDK - параллелограмм.
5. Самостоятельное решение задач (задачи выбирают учащиеся на интерактивной доске, решение сверяют с доской, перейдя по гиперссылке)
Обратно к выбору задач можно вернуться по гиперссылке.
6. Итог урока. Задание на дом.
Итак, подведём итог сегодняшнего урока. Ответьте, пожалуйста, на мои вопросы:
- Какими утверждениями являются по отношению друг к другу свойство и признак объекта?
- Сформулируйте признаки параллелограмма?
- Для чего нужны нам признаки параллелограмма?
Домашнее задание: п. 43, доказательство второго и третьего признака закончить, № 380, № 383.
7. Рефлексия.
У.: Ребята, мы сегодня изучили признаки параллелограмма, доказали их и мне хочется узнать, как вы поняли материал урока? (оставить на рабочем столе нужную полоску)