Цель:
1. Систематизация и обобщение изученного материала.
2. Выявление структурного сходства в формулах n-го члена, суммы n первых членов, характеристического свойства арифметической и геометрической прогрессий.
3.Фомирование логического мышления учащихся при решении задач повышенной трудности.
4. Развитие навыков самоконтроля.
Ход урока
I. Устный счёт. Повторение теоретического материала. (10 мин.)
Запись на диске: Прогрессио - движение вперёд.
Слово "прогрессия" латинского происхождения (progressio), буквально означает "движение вперёд" (как и слово "прогресс").
При устном счёте используется таблица (Cлайд-1 презентации. Приложение 1)
| А | В | С | D | |
| 1. | an = n | an = 2n-1 | a n = 7-n | an = |
| 2. | an = 2n | an = n2 | an = 2n | an = |
| 3. | а1 = 5, an+1 = - an |
a1 = 10, an+1 = an -1 |
a1 = 7, a n+1 = an +1 |
a1 = 3, an+1 = 2an |
1. Дайте определение арифметической прогрессии.
2. Есть ли среди последовательностей столбца А арифметические прогрессии? Если есть, то укажите её разность.
(А1, d = 1; А2 , d = 2).
3. В чём состоит характеристическое свойство арифметической прогрессии, которое отражено в её названии?
(Каждый член арифметической прогрессии,
начиная со второго, равен среднему
арифметическому последующего и предыдущего
членов: an = ![]() )
)
4. Проиллюстрируйте это свойство на примере арифметической прогрессии
(А2 2; 4; 6; 8; 10; 12;...
6 = (4+8): 2)
5. Какими бывают арифметические прогрессии в зависимости от её разности d? Приведите примеры возрастающей, убывающей, постоянной арифметической прогрессий.
6. Дайте определение геометрической прогрессии.
7. Среди последовательностей строки 3 есть ли геометрические прогрессии? Если есть, то укажите её знаменатель (А3, q = -1; D3, q = 2).
8. Откуда произошло название "геометрическая прогрессия"? Сформулируйте характеристическое свойство геометрической прогрессии. Проверьте его справедливость для прогрессии D3.
(Каждый член геометрической прогрессии с положительными членами, начиная со второго, равен среднему геометрическому последующего и предыдущего членов:
bn = ![]()
D3 , 3; 6; 12; 24; 48;. ..
( 6= ![]() )
)
9. Демонстрируется слайд-2 презентации (Приложение 1):
| b1 > 0 | b 1 < 0 | |
| q >1 | ||
| q =1 | ||
| 0< q <1 | ||
| q < 0 |
В каких случаях геометрическая прогрессия является возрастающей, в каких убывающей, в каких постоянна?
| b1 > 0 | b 1 < 0 | |
| q >1 | Возрастающая | Убывающая |
| q =1 | Постоянная | Постоянная |
| 0< q <1 | Убывающая | Возрастающая |
| q < 0 | - | - |
10. Запишите формулы n-го члена арифметической и геометрической прогрессий (2 ученика у доски).
( an = a1+d * (n-1)
bn = b1 * qn-1 )
11. Запишите формулы суммы n первых членов арифметической и геометрической прогрессий
(2 ученика у доски).
( Sn = ![]() *
n;
*
n;
Sn = ![]() ;
;
Sn = ![]() * n;
* n;
Sn = ![]() )
)
12.В каком случае можно найти сумму всех членов геометрической прогрессии? Запишите формулу для её вычисления.
( |q| < 1, S = ![]() )
)
13.Демострируется слайд-3 презентации (Приложение 1)
Задача очень непроста:
Как сделать, чтобы быстро
От единицы и до ста
Сложить в уме все числа?
Великий немецкий математик Карл Фридрих Гаусс вычислил в уме сумму всех натуральных чисел от 1 и до 100, когда ему было менее 10 лет.
1+2+3+...+50+51+...+98+99+100=101 * 50=5050
Объясните этот способ вычисления.
Пять первых связок изучи, -
Найдёшь к решению ключи!
- 1+100=?
- 2+99=?
- 3+98=?
- 4+97=?
- 5+96=?
Давным-давно один мудрец сказал,
Что прежде надо
Связать начало и конец
У численного ряда.
II. Самостоятельная работа (10 мин.)
(Проверка умения применения учащимися формул арифметической и геометрической прогрессий).
Каждый учащийся получает каточку с таблицей, которую надо заполнить:
Вариант - I.
| d | n | |||
| 3 | -2 | 5 | ||
| q | n | |||
| 20 | 4 | -2,5 |
Решение:
1) ![]() = 3+(-2) * (5-1) = 3-8 = -5
= 3+(-2) * (5-1) = 3-8 = -5
S5 = ![]() * 5=-1 * 5= -5
* 5=-1 * 5= -5
2) -2,5 = 20 * q3 , q3= ![]() = -
= -![]() , q= -0,5
, q= -0,5
S4 = ![]() =
= ![]() =
= ![]() =
= ![]() = 12,5.
= 12,5.
Вариант - II.
| а1 | d | n | аn | Sn |
| -4 | 7 | 10 | ||
| b1 | q | n | bn | Sn |
| 4 | - 1/4 | 4 |
Решение
1) 10 = - 4 + 7 * (n-1), S3 ![]() * 3 = 9
* 3 = 9
14 = 7 * (n-1),
2 = n-1,
n = 3.
2) bn = 4 * ![]() )3 =
4 * (-
)3 =
4 * (-![]() ) = -
) = - ![]()
S4 = ![]() =
= ![]() =
= ![]() =
= ![]() = 3
= 3![]() .
.
(Проверка самостоятельной работы проводится по аналогичным таблицам, но с ответами. (Сайды -3 ,4 презентации. Приложение 1)
Учащиеся, которые выполнили работу раньше остальных, могут быть использованы в роли консультантов).
III. Сообщение учителя (3 мин.)
Структурное сходство арифметической и геометрической прогрессий иллюстрируется с помощью таблицы "Прогрессии" (Слайд 5 презентации. Приложение 1).

Вы изучали две прогрессии - арифметическую и геометрическую. Вспомним их определения (сразу оба). Обратите внимание, насколько похожи определения. Надо заменить сложение умножением, или наоборот, и из одной прогрессии, получим другую. Родство прогрессий становится ещё более заметным, если вспомнить их характеристические свойства.
an = ![]() bn =
bn = ![]()
Здесь тоже достаточно заменить сложение умножением, а деление на 2 извлечением корня второй степени, и из характеристического свойства арифметической прогрессии получается характеристическое свойство геометрической прогрессии.
Сравним формулы n - х членов прогрессий.
Зная одну формулу, можно легко получить другую - надо лишь сложение заменить умножением и умножение заменить возведением в степень.
На связь между прогрессиями первым обратил внимание по-видимому, великий Архимед.
Сами по себе прогрессии известны так давно, что, конечно, нельзя говорить о том, кто их открыл. Ведь уже натуральный ряд 1, 2, 3, 4,..., n,.. есть арифметическая прогрессия с первым членом 1 и разностью, тоже равной 1. О том, как давно была известна геометрическая прогрессия, косвенным образом свидетельствует предание о создании шахмат.
IV. Решение задач (22 мин.)
Сейчас мы решим с вами одну из древнейших задач на прогрессии.
Индивидуальное сообщение учащегося. Он тоже выступает в роли второго учителя.
(12 мин.)
Древнейшая задача на прогрессии - не вопрос о вознаграждении изобретателя шахмат, начитывающий за собой двухтысячелетнюю давность, а гораздо более старая задача о делении хлеба, которая записана в знаменитом египетском папирусе Ринда. Папирус
этот, разысканный Риндом в конце прошлого столетия, составлен около 2000 лет до нашей эры и является списком с другого, ещё более древнего математического сочинения, относящегося, быть может, к третьему тысячелетию до нашей эры. В числе арифметических, алгебраических и геометрических задач этого документа имеется такая:
Сто мер хлеба разделить между пятью людьми так, чтобы второй получил на столько же больше первого, на сколько третий получил больше второго, четвертый больше третьего и пятый больше четвёртого. Кроме того, двое первых должны получить в 7 раз меньше трёх остальных. Сколько нужно дать каждому?
Решение:
Количества хлеба, полученные участниками раздела, составляют возрастающую арифметическую прогрессию. Пусть её первый член х, разность - y. Тогда
Доля I-го - x мер хлеба;
- II-го - (x + y);
- III-го - (x + 2y);
- VI-го - (x + 3y);
- V-го - (x + 4y).
Sn = ![]() * n; S5 =
* n; S5 = ![]() * 5 = (x+2y) * 5
* 5 = (x+2y) * 5
На основании условий задачи составляем следующие два уравнения:
![]()
![]()
![]()
![]()
![]()
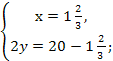

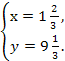
1![]() меры получил 1 - й
человек.
меры получил 1 - й
человек.
1) 1![]() + 9
+ 9![]() .= 10
.= 10![]() - 2 - й
человек.
- 2 - й
человек.
2) 10![]() + 9
+ 9![]() = 20 - 3 - й человек.
= 20 - 3 - й человек.
3) 20 + 9 ![]() = 29
= 29![]() - 4- й - человек.
- 4- й - человек.
4) 29![]() + 9
+ 9 ![]() = 38
= 38![]() - 5 - й
человек.
- 5 - й
человек.
Ответ: Хлеб должен быть разделён на части: 1![]() ; 10
; 10![]() ; 20; 29
; 20; 29![]() ; 38
; 38![]() .
.
2. Упростите выражение
1986 * (19871991 + 19871990 +:.+ 19872+ 1988) + 1 (5 мин.) (у доски)
Решение:
Сафронова Вера Николаевна 103-910-256
1986 * (19871991 + 19871990 + :+ 19872 + 1988) + 1 =
1986 * (19871991 + 19811990 + : + 19872+ 1987 +1) + 1 =
1986 * ![]() + 1= 1986*
+ 1= 1986* ![]() + 1 = 19871992 - 1 + 1 = 19871992
+ 1 = 19871992 - 1 + 1 = 19871992
Решите уравнение
(х2 + х + 1) + (х2 + 2х + 3) + (х2 + 3х + 5) +: + (х2 + 20х+39) = 4500
(с комментированием) - 5 мин.
Решение:
Слагаемые, стоящие в правой части уравнения, образуют арифметическую прогрессию с разностью d = х + 2. В этой прогрессии всего 20 членов (число нечётных чисел в последовательности 1, 2, 3,:, 39). По формуле для вычисления S20
найдём (х2 + х + 1+ х2 +20х + 39) : 2 * 20 = 4500,
2х2 + 21х + 40 - 450 = 0,
2х2 + 21х - 410 = 0.
D = 441 + 8 * 410 = 441 + 3280 = 3721 > 0,
х 1,2 = ( -21 + 61) : 4,
х 1= - 20,5,
х2 = 10.
V. Домашнее задание: задача
Задача:
В геометрической прогрессии ( bn ) сумма второго, третьего и четвёртого членов равна 7, а сумма четвёртого, пятого и шестого равна 28. Найдите
а) b6 + b7 + b8 ,
б) ![]() .
.
VI. Подведение итогов
Литература
1. Г.И. Глейзер "История математики в школе". VII - VIII классы - М., Просвещение. 1982.
2. Б.А. Кордемский, А.А. Ахадов "Удивительный мир чисел" - М., Просвещение. 1986.
3. Я.И. Перельман "Занимательная алгебра" - М., Наука. 1991.
4. Л.Ф. Пичурин "За страницами учебника алгебры" - М., Просвещение. 1990.
5. "Математика в школе". №6 1990 год (Стр. 41-43). №2 1991 год (Стр. 61-62).