Цели урока:
1. Обучающие:
- закрепить умения вычислять пределы функций;
- продолжить формирование умений применять непрерывность функций к решению различных задач.
2. Развивающие:
- развитие памяти учащихся; развитие умственных операций (обобщение, сравнение, анализ, синтез); развитие познавательного интереса;
- развитие психических процессов мышления, смысловой памяти, аргументированной речи, доказательного воспроизведения в процессе деятельности;
- развитие творческих способностей учащихся.
3. Воспитательные:
- воспитывать доброжелательность, дисциплинированность, взаимоуважение, трудолюбие;
- воспитывать ответственность за свой учебный труд; воспитывать культуру ученического труда;
- развитие эстетических норм и качеств.
Оборудование:
- мультимедийный проектор, графопроектор;
- карточки с заданиями для групп;
- слайды с выполненным домашним заданием;
- чистая плёнка для выполнения заданий;
- условия заданий на плакатах.
План урока:
- Организационный момент.
- Проверка домашнего задания.
- Устная работа.
- Работа в группах.
- Защита выполненных заданий.
- Итог урока, задание на дом.
Ход урока
1. Организационный момент.
Организую детей на урок, объявляю тему урока и ставлю цель перед учащимися.
Сегодня на уроке мы заканчиваем изучение темы «Непрерывность функции», поэтому каждому из вас предоставляется такая возможность: провести небольшое исследование и с полученными результатами познакомить нас.
2. Проверка домашнего задания.
Через мультимедийный проектор предлагается решение домашнего задания. Ребята, обменявшись тетрадями, проверяют и выставляют оценки.
3. Устная работа.
Восстановить в памяти определения:
3.1. Какая функция называется непрерывной в точке?
Функция называется непрерывной в точке а, если она определена в этой точке и её lim x→a f (x) = f (a).
3.2. Какая функция называется непрерывной на отрезке?
Если функция непрерывна в каждой точке отрезка, то она непрерывна на всём отрезке.
3.3. Если функции f (x) и g (x) непрерывны в точке а, то что можно сказать о их сумме, произведении и о частном?
f (x) + g
(x) – непрерывная функция; f (x) *
g (x) – непрерывная функция;
![]() – непрерывная функция,
если g (x) ≠ 0.
– непрерывная функция,
если g (x) ≠ 0.
3.4. Что вы можете сказать о непрерывности рациональной функции?
Рациональная функция непрерывна на области действительных чисел.
3.5. Что вы можете сказать о непрерывности дробно-рациональной функции?
Дробно-рациональная функция непрерывна на своей области определения.
3.6. Какими свойствами обладают непрерывные функции?
а) Если f (x) непрерывна на отрезке [a;b] и принимает на его концах значения разных знаков, то она обращается в нуль хотя бы в одной точке этого отрезка.
б) Если функция f (x) непрерывна на интервале (a;b) и не обращается в нуль ни в одной точке этого интервала, то она имеет один и тот же знак во всех точках данного интервала.
4. Работа в группах.
Класс разделён на группы по 4 человека. Каждой группе выдано задание. Учащиеся выполняют задания на плёнке и представляют его через графопроектор.
1 группа. Исследуйте функцию на непрерывность и постройте схематически график.
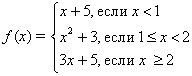
Решение. Каждая отдельная функция, входящая в исходную, непрерывна, следовательно, разрывы могут возникнуть лишь в точках, при переходе через которые одно выражение сменяется другим, т.е. в точках x = –1 и x = 2. Рассмотрим, как ведёт себя функция в окрестности точки x = –1.
1) x = –1
lim x→–1–(x + 5) = 4
lim x→–1+(x2 + 3) = 4
Следовательно, в точке x = –1 функция непрерывна.
2) x = 2
lim x→–2–(x2 + 3) = 7
lim x→–2+(3x + 5) = 11
Следовательно, в точке функция имеет разрыв I рода.
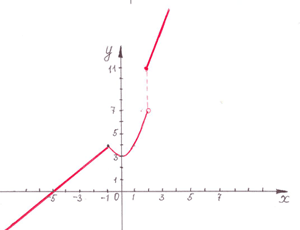
Рисунок 1
2 группа. Найдите область определения функции.
![]()
Решение. Так как арифметический квадратный корень
можно вычислить из неотрицательного числа, то
![]()
Вводим функцию
![]()
Находим нули функции f (x) = , тогда x2 + 7x + 12 = 0; по теореме Виета и обратной к ней:
x1 + x2= –7
x1 * x2= 12
получаем x1 = –3, x2 = –4
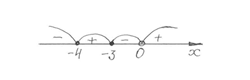
Рисунок 2
![]()
![]()
3 группа.
а) Докажите, что
![]()
б) Вычислите:
![]()
а) В знаменателе дроби под знаком предела стоит сумма
членов арифметической прогрессии, поэтому её можно записать как
![]() тогда
тогда

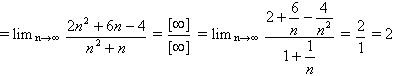
б) ![]()
![]()
4 группа. Докажите, что уравнение x3 – 3x + 1 имеет корень на отрезке [0; 1] и найдите его с точностью до 0,1.
Решение. Введём функцию f (x) = x3 – 3x + 1, она непрерывна на всей числовой прямой, а её значения f (0) = 1; f (1) = –1.Так как функция разных знаков на концах отрезка, то на этом интервале она может обратиться в нуль хотя бы в одной точке. Разобьем интервал [0; 1] на более мелкие отрезки и составим таблицу:
| x | 0 | 0,2 | 0,4 | 0,6 | 0,8 | 1 |
| f (x) | 1 | 0,408 | –0,135 | –0,584 | –0,888 | –1 |
Вывод. Так как функция меняет знак на отрезке [0,2; 0,4], то корень уравнения с точностью до 0,1 будет равен x = 0,3.
Ответ: x = 0,3.
5 группа. Решить неравенство:
![]()
Решение. Вводим функцию
![]()
Найдём нули функции f (x) = 0, следовательно, (x – 2)3(x + 5) = 0, тогда x = 2, x = –5.
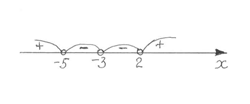
Рисунок 3
![]()
![]()
![]()
![]()
![]()
![]()
5. Защита выполненных работ.
6. Подведение итогов, задание на дом: №254(в, г); №250(в, г).